《2026年学易优高考二轮总复习数学》

(多选)(2025·邵阳模拟)已知函数 $ f(x) $ 与其导函数 $ g(x) $ 的定义域均为 $ \mathbf{R} $，且 $ f(x - 1) $ 和 $ g(2x + 1) $ 都是奇函数，且 $ g(0)=\frac{1}{3} $，则下列说法正确的有(ACD)

A.$ g(x) $ 关于 $ x = -1 $ 对称
B.$ f(x) $ 关于 $ (1,0) $ 对称
C.$ g(x) $ 是周期函数
D.$ \sum_{i = 1}^{12} i g(2i)=4 $

答案： 例3]ACD　因为f(x - 1)为奇函数，所以f(x - 1)=−f(−x - 1)，即f'(x - 1)=f'(−x - 1)，则g(x - 1)=g(−x - 1)，所以g(x)的图象关于直线x = −1对称，故A正确；因为f(x - 1)为奇函数，则其图象关于(0,0)对称，向左平移一个单位后得到f(x)的图象，则f(x)的图象关于(−1,0)对称，故B错误；因为g(2x + 1)为奇函数，则g(2x + 1)=−g(−2x + 1)，所以g(x)=−g(−x + 2)，①
又g(x - 1)=g(−x - 1)，
则g(x)=g(−x - 2)，②
由①②得g(x)=g(x + 8)，所以8是函数g(x)的一个周期，g(x)是周期函数，故C正确；因为g
(0)=$\frac{1}{3}$，g(x)=−g(−x + 2)，
所以g
(2)=−g(2 - 2)=−g
(0)=−$\frac{1}{3}$，g
(4)=−g
(0)=−$\frac{1}{3}$，g
(6)=−g
(2)=$\frac{1}{3}$，所以
$\sum_{i = 1}^{12} g(2i)=(-1 - 2 + 3 + 4 - 5 - 6 + 7 + 8 - 9 - 10 + 11 + 12) × \frac{1}{3}=4$，D正确. 故选ACD.

(1)(2025·乌鲁木齐质检)偶函数 $ f(x) $ 在区间 $ [0,+\infty) $ 上单调递增，且 $ f(1)=0 $，则不等式 $ f(2x - 3) ＞ 0 $ 的解集为(D)

A.$ (-2,-1) $
B.$ (-\infty,-2) \cup (-1,+\infty) $
C.$ (1,2) $
D.$ (-\infty,1) \cup (2,+\infty) $

答案：
(1)D　因为f(x)为偶函数，且在[0,+∞)上单调递增，所以结合对称性可得f(x)在(−∞,0]上单调递减，且f(−1)=f
(1)=0，若f(2x - 3)＞0，则2x - 3＞1或2x - 3＜−1，故x＞2或x＜1，故选D.

(2)已知定义在 $ \mathbf{R} $ 上的偶函数 $ f(x) $ 满足 $ f(x + 6)=f(x) $，且当 $ x \in [0,3] $ 时，$ f(x)=x \mathrm{e}^{x} $，则下面结论正确的是(A)

A.$ f(\ln 3) ＜ f\left(\mathrm{e}^{3}\right) ＜ f(-\mathrm{e}) $
B.$ f(-\mathrm{e}) ＜ f(\ln 3) ＜ f\left(\mathrm{e}^{3}\right) $
C.$ f\left(\mathrm{e}^{3}\right) ＜ f(-\mathrm{e}) ＜ f(\ln 3) $
D.$ f(\ln 3) ＜ f(-\mathrm{e}) ＜ f\left(\mathrm{e}^{3}\right) $

答案：
(2)A
∵x∈[0,3]，f(x)=xe^x，
∴f'(x)=e^x(x + 1)且f'(x)＞0，
∴x∈[0,3]时，f(x)单调递增；
∵f(x + 6)=f(x)，
∴x∈[18,21]时，f(x)单调递增；
∵2 + 3 × 6＜e³＜e + 3 × 6，
∴f(2 + 3 × 6)＜f(e³)＜f(e + 3 × 6)，
∴f
(2)＜f(e³)＜f(e).
∵f(−x)=f(x)，
∴f(−e)=f(e)，
∵0＜ln3＜lne² = 2，
∴f(ln3)＜f
(2).
综上所述，
f(ln3)＜f(e³)＜f(−e).
故选A.

(1)(2025·天津二模)函数 $ f(x)=\cos x + 2\cos 2x + 3\cos 3x $ 的大致图象可能是(A)

答案：
(1)A　f(x)的定义域为$\mathbf{R}$，则f(−x)=cos(−x)+2cos(−2x)+3cos(−3x)=cosx+2cos2x+3cos3x = f(x)，所以f(x)为偶函数，图象关于y轴对称，故排除C，D选项；又因为f
(0)=6，故排除B选项.故选A.

(2)(多选)已知函数 $ f(x)=\left\{\begin{array}{l}-x^{2}-4x,x \leqslant 0, \\ |\log _{2} x|,x ＞ 0,\end{array}\right. $ 若 $ x_{1} ＜ x_{2} ＜ x_{3} ＜ x_{4} $，且 $ f\left(x_{1}\right)=f\left(x_{2}\right)=f\left(x_{3}\right)=f\left(x_{4}\right) $，则下列结论正确的是(AB)

A.$ x_{1}+x_{2}=-4 $
B.$ x_{3} x_{4}=1 $
C.$ 1 ＜ x_{4} ＜ 4 $
D.$ 0 ＜ x_{1} x_{2} x_{3} x_{4} \leqslant 4 $

答案：

(2)AB　函数f(x)=$\begin{cases}-x^2 - 4x, x \leq 0 \\ |\log_2 x|, x ＞ 0\end{cases}$的图象如图所示，

设f(x₁)=f(x₂)=f(x₃)=f(x₄)=t，则0＜t＜4，则直线y = t与函数y = f(x)图象的4个交点横坐标分别为x₁,x₂,x₃,x₄，函数y = −x²−4x的图象关于直线x = −2对称，则x₁ + x₂ = −4，故A正确；由图象可知|log₂x₃|=|log₂x₄|，且0＜x₃＜1＜x₄，所以−log₂x₃ = log₂x₄，即log₂(x₃x₄)=0，所以x₃x₄ = 1，故B正确；由图象可知log₂x₄∈(0,4)，则1＜x₄＜16，故C错误；由图象可知−4＜x₁＜−2，所以x₁x₂x₃x₄=x₁(−4−x₁)=−x₁²−4x₁=−(x₁ + 2)²+4∈(0,4)，故D错误.

(1)(2025·南充模拟)已知函数 $ f(x)=\frac{x \cos x}{\mathrm{e}^{x}+\mathrm{e}^{-x}} $，则函数 $ y = f(x - 1)+1 $ 的图象(A)

A.关于点 $ (1,1) $ 对称
B.关于点 $ (-1,1) $ 对称
C.关于点 $ (-1,0) $ 对称
D.关于点 $ (1,0) $ 对称

答案：
(1)A　因为f(x)=$\frac{x \cos x}{e^x + e^{-x}}$，所以f(−x)=$\frac{-x \cos x}{e^{-x} + e^x}$=−f(x)，又f(x)的定义域为$\mathbf{R}$，所以f(x)的图象关于原点对称，函数y = f(x - 1) + 1的图象可由f(x)的图象，先向右平移一个单位长度，再向上平移一个单位长度得到，所以函数y = f(x - 1) + 1的图象关于点(1,1)对称.

(2)(2025·西安质检)已知函数 $ y = f(x) $ 是定义域为 $ \mathbf{R} $ 的奇函数，当 $ x \in (0,3) \cup (3,+\infty) $ 时，$ f(-x) ＞ 2 f(x) $，$ f(3)=0 $，则不等式 $ f(x) ＞ 0 $ 的解集为(−∞,−3)∪(−3,0) 。

答案：

(2)(−∞,−3)∪(−3,0)　依题意知，f
(0)=0，
当x∈(0,3)∪(3,+∞)时，f(−x)＞2f(x)，即−f(x)＞2f(x)，得f(x)＜0，
由f
(3)=0，得f(−3)=−f
(3)=0，
由此画出f(x)的可能图象如图所示，

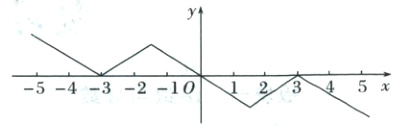
由图可知，不等式f(x)＞0的解集为(−∞,−3)∪(−3,0).