2026年学易优高考二轮总复习数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优高考二轮总复习数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
训练 3 (1)(多选)(2025·温州模拟)若圆 $C$ 与直线 $3x - 4y - 12 = 0$ 相切,且与圆 $x^{2}-2x + y^{2}=0$ 相切于点 $A(2,0)$,则圆 $C$ 的半径为(
A.5
B.3
C.$\frac{5}{3}$
D.$\frac{3}{4}$
BD
)A.5
B.3
C.$\frac{5}{3}$
D.$\frac{3}{4}$
答案:
训练3
(1)BD 圆$x^2 - 2x + y^2 = 0$的圆心为$(1,0)$,半径为$1$。圆$C$与圆$x^2 - 2x + y^2 = 0$相切于点$A(2,0)$,则圆心在$x$轴,设圆心为$(a,0)$。
则由题意$\vert a - 2\vert = \frac{\vert 3a - 12\vert}{5}$,
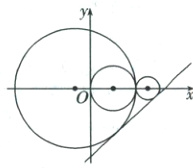
解得$a = -1$或$a = \frac{11}{4}$。
$a = -1$时,半径为$\vert -1 - 2\vert = 3$;$a = \frac{11}{4}$时,半径为$\vert \frac{11}{4} - 2\vert = \frac{3}{4}$。故选BD。
训练3
(1)BD 圆$x^2 - 2x + y^2 = 0$的圆心为$(1,0)$,半径为$1$。圆$C$与圆$x^2 - 2x + y^2 = 0$相切于点$A(2,0)$,则圆心在$x$轴,设圆心为$(a,0)$。
则由题意$\vert a - 2\vert = \frac{\vert 3a - 12\vert}{5}$,

解得$a = -1$或$a = \frac{11}{4}$。
$a = -1$时,半径为$\vert -1 - 2\vert = 3$;$a = \frac{11}{4}$时,半径为$\vert \frac{11}{4} - 2\vert = \frac{3}{4}$。故选BD。
(2)(2025·四川·三模)已知圆 $C:x^{2}+y^{2}-2x + 4y - 20 = 0$ 上恰有两个点到直线 $l:x + y + m = 0(m>0)$ 的距离为 2,则 $m$ 的取值范围是(
A.$(3\sqrt{2},7\sqrt{2})$
B.$(3\sqrt{2}+1,7\sqrt{2}+1)$
C.$(2\sqrt{2},7\sqrt{2})$
D.$(2\sqrt{2}+1,7\sqrt{2}+1)$
B
)A.$(3\sqrt{2},7\sqrt{2})$
B.$(3\sqrt{2}+1,7\sqrt{2}+1)$
C.$(2\sqrt{2},7\sqrt{2})$
D.$(2\sqrt{2}+1,7\sqrt{2}+1)$
答案:
(2)B 由题意可得圆$C:(x - 1)^2 + (y + 2)^2 = 25$,则圆心$C(1, - 2)$,半径$r = 5$,则圆心$C$到直线$l$的距离$d = \frac{\vert m - 1\vert}{\sqrt{2}}$。因为圆$C$上恰有两个点到直线$l$的距离为$2$,所以$r - 2 < d < r + 2$,即$3 < \frac{\vert m - 1\vert}{\sqrt{2}} < 7$,又$m > 0$,解得$3\sqrt{2} + 1 < m < 7\sqrt{2} + 1$。故选B。
(2)B 由题意可得圆$C:(x - 1)^2 + (y + 2)^2 = 25$,则圆心$C(1, - 2)$,半径$r = 5$,则圆心$C$到直线$l$的距离$d = \frac{\vert m - 1\vert}{\sqrt{2}}$。因为圆$C$上恰有两个点到直线$l$的距离为$2$,所以$r - 2 < d < r + 2$,即$3 < \frac{\vert m - 1\vert}{\sqrt{2}} < 7$,又$m > 0$,解得$3\sqrt{2} + 1 < m < 7\sqrt{2} + 1$。故选B。
例 5 (1)已知直线 $kx - y + 2k = 0$ 与直线 $x + ky - 2 = 0$ 相交于点 $P$,点 $A(4,0)$,$O$ 为坐标原点,则 $\tan\angle OAP$ 的最大值为(
A.$2-\sqrt{3}$
B.$\frac{\sqrt{3}}{3}$
C.1
D.$\sqrt{3}$
B
)A.$2-\sqrt{3}$
B.$\frac{\sqrt{3}}{3}$
C.1
D.$\sqrt{3}$
答案:
例5
(1)B 直线$kx - y + 2k = 0$恒过定点$M(-2,0)$,直线$x + ky - 2 = 0$恒过定点$N(2,0)$。又易知两直线垂直,故$P$点轨迹是以$(0,0)$为圆心,$2$为半径的圆,除去与$x$轴的交点,于是得$x^2 + y^2 = 4(x \neq \pm 2)$。
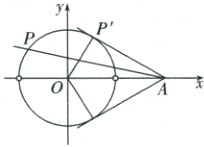
如图,观察图形可知,射线$AP$绕点$A$旋转$\angle OAP \in (0,\frac{\pi}{2})$,当旋转到与圆$O:x^2 + y^2 = 4$相切时,$\angle OAP$最大。因为$\vert OA\vert = 4$,$AP'$为切线,点$P'$为切点,$\vert OP'\vert = 2$,$\angle OP'A = \frac{\pi}{2}$,则$\angle OAP' = \frac{\pi}{6}$,所以$\angle OAP$最大值为$\frac{\pi}{6}$,所以$(\tan\angle OAP)_{\max} = \tan\frac{\pi}{6} = \frac{\sqrt{3}}{3}$。
例5
(1)B 直线$kx - y + 2k = 0$恒过定点$M(-2,0)$,直线$x + ky - 2 = 0$恒过定点$N(2,0)$。又易知两直线垂直,故$P$点轨迹是以$(0,0)$为圆心,$2$为半径的圆,除去与$x$轴的交点,于是得$x^2 + y^2 = 4(x \neq \pm 2)$。

如图,观察图形可知,射线$AP$绕点$A$旋转$\angle OAP \in (0,\frac{\pi}{2})$,当旋转到与圆$O:x^2 + y^2 = 4$相切时,$\angle OAP$最大。因为$\vert OA\vert = 4$,$AP'$为切线,点$P'$为切点,$\vert OP'\vert = 2$,$\angle OP'A = \frac{\pi}{2}$,则$\angle OAP' = \frac{\pi}{6}$,所以$\angle OAP$最大值为$\frac{\pi}{6}$,所以$(\tan\angle OAP)_{\max} = \tan\frac{\pi}{6} = \frac{\sqrt{3}}{3}$。
(2)在平面直角坐标系 $xOy$ 中,已知圆 $C:(x - a)^{2}+(y - a + 2)^{2}=1$,点 $A(0,2)$,若圆 $C$ 上存在点 $M$,满足 $\vert MA\vert^{2}+\vert MO\vert^{2}=10$,则实数 $a$ 的取值范围是
[0,3]
。
答案:
(2)$[0,3]$ 设$M(x,y)$,由$\vert MA\vert^2 + \vert MO\vert^2 = 10$可得$x^2 + (y - 2)^2 + x^2 + y^2 = 10$,即$x^2 + (y - 1)^2 = 4$,则点$M$在圆$x^2 + (y - 1)^2 = 4$上。
由题目条件可知点$M$在圆$C:(x - a)^2 + (y - a + 2)^2 = 1$上,所以两圆相交或相切,则$2 - 1 \leq \sqrt{(a - 0)^2 + (a - 2 - 1)^2} \leq 1 + 2$,解得$0 \leq a \leq 3$。
(2)$[0,3]$ 设$M(x,y)$,由$\vert MA\vert^2 + \vert MO\vert^2 = 10$可得$x^2 + (y - 2)^2 + x^2 + y^2 = 10$,即$x^2 + (y - 1)^2 = 4$,则点$M$在圆$x^2 + (y - 1)^2 = 4$上。
由题目条件可知点$M$在圆$C:(x - a)^2 + (y - a + 2)^2 = 1$上,所以两圆相交或相切,则$2 - 1 \leq \sqrt{(a - 0)^2 + (a - 2 - 1)^2} \leq 1 + 2$,解得$0 \leq a \leq 3$。
训练 4 (多选)(2025·盐城调研)在平面直角坐标系中,存在三点 $A(-1,0)$,$B(1,0)$,$C(0,7)$,动点 $P$ 满足 $\vert PA\vert=\sqrt{2}\vert PB\vert$,则(
A.点 $P$ 的轨迹方程为 $(x - 3)^{2}+y^{2}=8$
B.$\triangle PAB$ 面积最大时,$\vert PA\vert=2\sqrt{6}$
C.$\angle PAB$ 最大时,$\vert PA\vert=2\sqrt{6}$
D.$P$ 到直线 $AC$ 距离的最小值为 $\frac{4\sqrt{2}}{5}$
ABD
)A.点 $P$ 的轨迹方程为 $(x - 3)^{2}+y^{2}=8$
B.$\triangle PAB$ 面积最大时,$\vert PA\vert=2\sqrt{6}$
C.$\angle PAB$ 最大时,$\vert PA\vert=2\sqrt{6}$
D.$P$ 到直线 $AC$ 距离的最小值为 $\frac{4\sqrt{2}}{5}$
答案:
训练4 ABD 设$P(x,y)$,由$\vert PA\vert = \sqrt{2}\vert PB\vert$得$\vert PA\vert^2 = 2\vert PB\vert^2$,即$(x + 1)^2 + y^2 = 2[(x - 1)^2 + y^2]$,化简可得$(x - 3)^2 + y^2 = 8$,即点$P$的轨迹方程为$(x - 3)^2 + y^2 = 8$,A正确。
因为直线$AB$过圆$(x - 3)^2 + y^2 = 8$的圆心,所以点$P$到直线$AB$的距离的最大值为圆$(x - 3)^2 + y^2 = 8$的半径$r$,即为$2\sqrt{2}$。因为$\vert AB\vert = 2$,所以$\triangle PAB$面积最大为$\frac{1}{2} × 2 × 2\sqrt{2} = 2\sqrt{2}$,此时$P(3, \pm 2\sqrt{2})$,所以$\vert PA\vert = \sqrt{(3 + 1)^2 + (2\sqrt{2})^2} = 2\sqrt{6}$,B正确。
当$\angle PAB$最大时,则$PA$为圆$(x - 3)^2 + y^2 = 8$的切线,所以$\vert PA\vert = \sqrt{(3 + 1)^2 - 8} = 2\sqrt{2}$,C错误。
直线$AC$的方程为$7x - y + 7 = 0$,则圆心$(3,0)$到直线$AC$的距离为$\frac{\vert 7 × 3 - 0 + 7\vert}{\sqrt{7^2 + 1}} = \frac{14\sqrt{2}}{5}$,所以点$P$到直线$AC$距离的最小值为$\frac{14\sqrt{2}}{5} - 2\sqrt{2} = \frac{4\sqrt{2}}{5}$,D正确。
因为直线$AB$过圆$(x - 3)^2 + y^2 = 8$的圆心,所以点$P$到直线$AB$的距离的最大值为圆$(x - 3)^2 + y^2 = 8$的半径$r$,即为$2\sqrt{2}$。因为$\vert AB\vert = 2$,所以$\triangle PAB$面积最大为$\frac{1}{2} × 2 × 2\sqrt{2} = 2\sqrt{2}$,此时$P(3, \pm 2\sqrt{2})$,所以$\vert PA\vert = \sqrt{(3 + 1)^2 + (2\sqrt{2})^2} = 2\sqrt{6}$,B正确。
当$\angle PAB$最大时,则$PA$为圆$(x - 3)^2 + y^2 = 8$的切线,所以$\vert PA\vert = \sqrt{(3 + 1)^2 - 8} = 2\sqrt{2}$,C错误。
直线$AC$的方程为$7x - y + 7 = 0$,则圆心$(3,0)$到直线$AC$的距离为$\frac{\vert 7 × 3 - 0 + 7\vert}{\sqrt{7^2 + 1}} = \frac{14\sqrt{2}}{5}$,所以点$P$到直线$AC$距离的最小值为$\frac{14\sqrt{2}}{5} - 2\sqrt{2} = \frac{4\sqrt{2}}{5}$,D正确。
1. (2025·北京卷)抛物线 $ y^{2}=2px(p>0) $ 的顶点到焦点的距离为 3,则 $ p= $
6
。
答案:
1. 6 因为抛物线的顶点到焦点的距离为$\frac{p}{2}$,故$\frac{p}{2}=3$,故$p = 6$。故答案为 6。
2. (2025·北京卷)双曲线 $ x^{2}-4y^{2}=4 $ 的离心率为(
A.$ \dfrac{\sqrt{3}}{2} $
B.$ \dfrac{\sqrt{5}}{2} $
C.$ \dfrac{5}{4} $
D.$ \sqrt{5} $
B
)A.$ \dfrac{\sqrt{3}}{2} $
B.$ \dfrac{\sqrt{5}}{2} $
C.$ \dfrac{5}{4} $
D.$ \sqrt{5} $
答案:
2. B 由$x^{2}-4y^{2}=4$得,$\frac{x^{2}}{4}-y^{2}=1$,所以$a^{2}=4$,$b^{2}=1$,$c^{2}=a^{2}+b^{2}=5$,即$a = 2$,$c = \sqrt{5}$,所以$e = \frac{c}{a} = \frac{\sqrt{5}}{2}$。故选 B。
3. (2025·全国一卷)已知双曲线 $ C $ 的虚轴长是实轴长的 $ \sqrt{7} $ 倍,则 $ C $ 的离心率为(
A.$ \sqrt{2} $
B.2
C.$ \sqrt{7} $
D.$ 2\sqrt{2} $
D
)A.$ \sqrt{2} $
B.2
C.$ \sqrt{7} $
D.$ 2\sqrt{2} $
答案:
3. D 双曲线离心率十基本量计算 依题意得$b = \sqrt{7}a$,又$c^{2}=a^{2}+b^{2}$,所以$c^{2}=a^{2}+(\sqrt{7}a)^{2}=8a^{2}$,即$c = 2\sqrt{2}a$,故$e = 2\sqrt{2}$。故选 D。
4. (2025·全国二卷)设抛物线 $ C:y^{2}=2px(p>0) $ 的焦点为 $ F $,点 $ A $ 在 $ C $ 上,过 $ A $ 作 $ C $ 的准线的垂线,垂足为 $ B $,若直线 $ BF $ 的方程为 $ y=-2x+2 $,则 $ |AF|= $(
A.3
B.4
C.5
D.6
C
)A.3
B.4
C.5
D.6
答案:
4. C 直线与抛物线的位置关系 根据直线$y = -2x + 2$得$F(1,0)$,所以$C$的准线方程为$x = -1$,$C$的方程为$y^{2}=4x$,所以$B(-1,4)$,所以$A(4,4)$,所以$|AF| = |AB| = 5$。
查看更多完整答案,请扫码查看


