《2026年学易优高考二轮总复习数学》

训练 2 (1)(多选)(2025·连云港调研)设 $ \boldsymbol{a} $，$ \boldsymbol{b} $，$ \boldsymbol{c} $是三个非零向量，且相互不共线，则下列说法正确的是(AB)
A.若 $ |\boldsymbol{a} + \boldsymbol{b}| = |\boldsymbol{a} - \boldsymbol{b}| $，则 $ \boldsymbol{a} \perp \boldsymbol{b} $
B.若 $ |\boldsymbol{a}| = |\boldsymbol{b}| $，则 $ (\boldsymbol{a} + \boldsymbol{b}) \perp (\boldsymbol{a} - \boldsymbol{b}) $
C.若 $ \boldsymbol{a} · \boldsymbol{c} = \boldsymbol{b} · \boldsymbol{c} $，则 $ \boldsymbol{a} - \boldsymbol{b} $不与 $ \boldsymbol{c} $垂直
D.$ (\boldsymbol{b} · \boldsymbol{c})\boldsymbol{a} - (\boldsymbol{a} · \boldsymbol{c})\boldsymbol{b} $不与 $ \boldsymbol{c} $垂直

答案：
(1)AB $a$，$b$，$c$是三个非零向量，$\vert a + b\vert=\vert a - b\vert$两边平方得$(a + b)^{2}=(a - b)^{2}$，即$a^{2}+2a· b + b^{2}=a^{2}-2a· b + b^{2}$，
故$a· b = 0$，则$a\perp b$，故A正确;
$(a + b)·(a - b)=\vert a\vert^{2}-\vert b\vert^{2}=\vert a\vert^{2}-\vert b\vert^{2}$，因为$\vert a\vert=\vert b\vert$，
所以$(a + b)·(a - b)=0$，故$(a + b)\perp(a - b)$，故B正确;
$a· c = b· c$，
故$a· c - b· c=(a - b)· c = 0$，
又$a$与$b$不共线，有$a\neq b$，
则$a - b$与$c$垂直，故C错误;
$[(b· c)a-(a· c)b]· c=(b· c)(a· c)-(a· c)(b· c)=0$，故$(b· c)a-(a· c)b$与$c$垂直，故D错误.

(2)(2025·济南质检)平行四边形 $ ABCD $中，$ AB = 3 $，$ AD = 4 $，$ \angle BAD = \frac{\pi}{3} $，若 $ \overrightarrow{BE} = \overrightarrow{EC} $，$ \overrightarrow{CF} = 2\overrightarrow{FD} $，则 $ \overrightarrow{AE} · \overrightarrow{AF} = $(C)

A.4
B.6
C.18
D.22

答案：

(2)C 由题意可知，以A为坐标原点，建立平面直角坐标系如图所示.
因为$AB = 3$，$AD = 4$，$\angle BAD=\frac{\pi}{3}$，
所以$A(0,0)$，$B(3,0)$，$C(5,2\sqrt{3})$，$D(2,2\sqrt{3})$.
设$E(x,y)$，则$\overrightarrow{BE}=(x - 3,y)$，$\overrightarrow{EC}=(5 - x,2\sqrt{3}-y)$，由$\overrightarrow{BE}=\overrightarrow{EC}$，得$(x - 3,y)=(5 - x,2\sqrt{3}-y)$，即$\begin{cases}x - 3 = 5 - x,\\y = 2\sqrt{3}-y,\end{cases}$解得$\begin{cases}x = 4,\\y = \sqrt{3},\end{cases}$所以$E(4,\sqrt{3})$. 设$F(x_{1},y_{1})$，则$\overrightarrow{CF}=(x_{1}-5,y_{1}-2\sqrt{3})$，$\overrightarrow{FD}=(2 - x_{1},2\sqrt{3}-y_{1})$，由$\overrightarrow{CF}=2\overrightarrow{FD}$，得$(x_{1}-5,y_{1}-2\sqrt{3})=2(2 - x_{1},2\sqrt{3}-y_{1})$，即$\begin{cases}x_{1}-5 = 4 - 2x_{1},\\y_{1}-2\sqrt{3}=4\sqrt{3}-2y_{1},\end{cases}$解得$\begin{cases}x_{1}=3,\\y_{1}=2\sqrt{3},\end{cases}$
所以$F(3,2\sqrt{3})$. 所以$\overrightarrow{AE}=(4,\sqrt{3})$，$\overrightarrow{AF}=(3,2\sqrt{3})$，$\overrightarrow{AE}·\overrightarrow{AF}=(4,\sqrt{3})·(3,2\sqrt{3})=4×3+\sqrt{3}×2\sqrt{3}=18$. 故选C.

例 3 已知 $ \omega ＞ 0 $，$ \boldsymbol{a} = (\sqrt{3}\sin\omega x, -\cos\omega x) $，$ \boldsymbol{b} = (\cos\omega x, \cos\omega x) $，$ f(x) = \boldsymbol{a} · \boldsymbol{b} $，$ x_1 $，$ x_2 $是 $ y = f(x) - \frac{1}{2} $的两个零点，且 $ |x_1 - x_2|_{\min} = \pi $。
(1)求 $ f(x) $的单调递增区间；
(2)若 $ \alpha \in (0, \frac{\pi}{2}) $，$ f(\frac{\alpha}{2}) = \frac{1}{10} $，求 $ \sin2\alpha $的值。

答案： 解:
(1)$f(x)=\sqrt{3}\sin\omega x\cos\omega x-\cos^{2}\omega x=\frac{\sqrt{3}}{2}\sin2\omega x-\frac{1}{2}\cos2\omega x-\frac{1}{2}=\sin(2\omega x-\frac{\pi}{6})-\frac{1}{2}$
$\because x_{1}$，$x_{2}$是函数$y = f(x)-\frac{1}{2}=\sin(2\omega x-\frac{\pi}{6})-1$的两个零点，
即$x_{1}$，$x_{2}$是方程$\sin(2\omega x-\frac{\pi}{6}) = 1$的两个实根，
且$\vert x_{1}-x_{2}\vert_{\min}=\pi$，
$\therefore T=\frac{2\pi}{2\omega}=\pi$，$\therefore\omega = 1$.
$\therefore f(x)=\sin(2x-\frac{\pi}{6})-\frac{1}{2}$.
由$-\frac{\pi}{2}+2k\pi\leqslant2x-\frac{\pi}{6}\leqslant\frac{\pi}{2}+2k\pi$，$k\in\mathbf{Z}$，
得$-\frac{\pi}{6}+k\pi\leqslant x\leqslant\frac{\pi}{3}+k\pi$，$k\in\mathbf{Z}$.
$\therefore f(x)$的单调递增区间为$[-\frac{\pi}{6}+k\pi,\frac{\pi}{3}+k\pi](k\in\mathbf{Z})$.
(2)$f(\frac{\alpha}{2})=\sin(\alpha-\frac{\pi}{6})-\frac{1}{2}=\frac{1}{10}$，
$\therefore\sin(\alpha-\frac{\pi}{6})=\frac{3}{5}$.
$\because0\lt\alpha\lt\frac{\pi}{2}$，$\therefore-\frac{\pi}{6}\lt\alpha-\frac{\pi}{6}\lt\frac{\pi}{3}$
$\therefore\cos(\alpha-\frac{\pi}{6})=\frac{4}{5}$.
$\because\sin\alpha=\sin[(\alpha-\frac{\pi}{6})+\frac{\pi}{6}]=\sin(\alpha-\frac{\pi}{6})\cos\frac{\pi}{6}+\cos(\alpha-\frac{\pi}{6})\sin\frac{\pi}{6}=\frac{4 + 3\sqrt{3}}{10}$，
$\cos\alpha=\cos[(\alpha-\frac{\pi}{6})+\frac{\pi}{6}]=\cos(\alpha-\frac{\pi}{6})\cos\frac{\pi}{6}-\sin(\alpha-\frac{\pi}{6})\sin\frac{\pi}{6}=\frac{4\sqrt{3}-3}{10}$，
$\therefore\sin2\alpha=2\sin\alpha\cos\alpha=2×\frac{4 + 3\sqrt{3}}{10}×\frac{4\sqrt{3}-3}{10}=\frac{24 + 7\sqrt{3}}{50}$

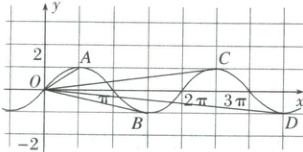
训练 3 (2025·武汉统考)如图所示，$ A $，$ B $，$ C $，$ D $是正弦函数 $ y = \sin x $图象上四个点，且在 $ A $，$ C $两点函数值最大，在 $ B $，$ D $两点函数值最小，则 $ (\overrightarrow{OA} + \overrightarrow{OB}) · (\overrightarrow{OC} + \overrightarrow{OD}) = $12\pi^{2}。

答案： 训练3 $12\pi^{2}$ 由题图知，$A(\frac{\pi}{2},1)$，$B(\frac{3\pi}{2}, - 1)$，$C(\frac{5\pi}{2},1)$，$D(\frac{7\pi}{2}, - 1)$，
所以$\overrightarrow{OA}=(\frac{\pi}{2},1)$，$\overrightarrow{OB}=(\frac{3\pi}{2}, - 1)$，$\overrightarrow{OC}=(\frac{5\pi}{2},1)$，$\overrightarrow{OD}=(\frac{7\pi}{2}, - 1)$，
所以$\overrightarrow{OA}+\overrightarrow{OB}=(2\pi,0)$，$\overrightarrow{OC}+\overrightarrow{OD}=(6\pi,0)$，
所以$(\overrightarrow{OA}+\overrightarrow{OB})·(\overrightarrow{OC}+\overrightarrow{OD})=2\pi×6\pi+0×0 = 12\pi^{2}$.

1. (2025·北京卷)已知平面直角坐标系 $xOy$ 中，$\vert \overrightarrow{OA}\vert =\vert \overrightarrow{OB}\vert =\sqrt{2}$，$\vert \overrightarrow{AB}\vert =2$，设 $C(3,4)$，则$\vert 2\overrightarrow{CA}+\overrightarrow{AB}\vert$的取值范围是(D)

A.$[6,14]$
B.$[6,12]$
C.$[8,14]$
D.$[8,12]$

答案： 1.D 因为$\vert\overrightarrow{OA}\vert=\vert\overrightarrow{OB}\vert=\sqrt{2}$，$\vert\overrightarrow{AB}\vert=2$，由$\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}$平方可得，$\overrightarrow{OA}·\overrightarrow{OB}=0$，所以$\langle\overrightarrow{OA},\overrightarrow{OB}\rangle=\frac{\pi}{2}$。
$2\overrightarrow{CA}+\overrightarrow{AB}=2(\overrightarrow{OA}-\overrightarrow{OC})+\overrightarrow{OB}-\overrightarrow{OA}=\overrightarrow{OA}+\overrightarrow{OB}-2\overrightarrow{OC}$，
$\vert\overrightarrow{OC}\vert=\sqrt{3^{2}+4^{2}}=5$，
所以$\vert2\overrightarrow{CA}+\overrightarrow{AB}\vert^{2}=\overrightarrow{OA}^{2}+\overrightarrow{OB}^{2}+4\overrightarrow{OC}^{2}-4(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}$
$=2 + 2 + 4×25 - 4(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}=104 - 4(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}$，
又$\vert(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}\vert\leq\vert\overrightarrow{OA}+\overrightarrow{OB}\vert\vert\overrightarrow{OC}\vert=5×\sqrt{2 + 2}=10$，即$-10\leq(\overrightarrow{OA}+\overrightarrow{OB})·\overrightarrow{OC}\leq10$，
所以$\vert2\overrightarrow{CA}+\overrightarrow{AB}\vert^{2}\in[64,144]$，即$\vert2\overrightarrow{CA}+\overrightarrow{AB}\vert\in[8,12]$。故选D。

2. (2023·全国乙卷)已知$\odot O$的半径为 $1$，直线 $PA$ 与$\odot O$相切于点 $A$，直线 $PB$ 与$\odot O$交于 $B$，$C$ 两点，$D$ 为 $BC$ 的中点，若$\vert PO\vert =\sqrt{2}$，则$\overrightarrow{PA}· \overrightarrow{PD}$的最大值为(A)

A.$\frac{1+\sqrt{2}}{2}$
B.$\frac{1+2\sqrt{2}}{2}$
C.$1+\sqrt{2}$
D.$2+\sqrt{2}$

答案： 2.A 解法一 连接$OA$，由题可知$\vert OA\vert=1$，$OA\perp PA$，因为$\vert OP\vert=\sqrt{2}$，所以由勾股定理可得$\vert PA\vert=1$，则$\angle POA=\frac{\pi}{4}$。设直线$OP$绕点$P$按逆时针旋转$\theta$后与直线$PD$重合，则$-\frac{\pi}{4}＜\theta＜\frac{\pi}{4}$，$\angle APD=\frac{\pi}{4}+\theta$，且$\vert PD\vert=\sqrt{2}\cos\theta$。
所以$\overrightarrow{PA}·\overrightarrow{PD}=\vert\overrightarrow{PA}\vert\vert\overrightarrow{PD}\vert\cos(\frac{\pi}{4}+\theta)$
$=\sqrt{2}\cos\theta\cos(\frac{\pi}{4}+\theta)=\sqrt{2}\cos\theta(\frac{\sqrt{2}}{2}\cos\theta-\frac{\sqrt{2}}{2}\sin\theta)$
$=\cos^{2}\theta-\sin\theta\cos\theta=\frac{1}{2}+\frac{1}{2}\cos2\theta-\frac{1}{2}\sin2\theta$
$=\frac{1}{2}+\frac{\sqrt{2}}{2}\cos(2\theta+\frac{\pi}{4})\leq\frac{1}{2}+\frac{\sqrt{2}}{2}$，故选A。
解法二 以圆心$O$为坐标原点建立平面直角坐标系，设圆$O$：$x^{2}+y^{2}=1$，点$P(\sqrt{2},0)$，因为$\vert OA\vert=1$，且$OA\perp PA$，所以$\angle POA=\frac{\pi}{4}$，不妨设$A(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$。
设直线$PD$的方程为$y=k(x - \sqrt{2})$，$B(x_{1},y_{1})$，$C(x_{2},y_{2})$，
由$\begin{cases}y=k(x - \sqrt{2})\\x^{2}+y^{2}=1\end{cases}$
得$(k^{2}+1)x^{2}-2\sqrt{2}k^{2}x+2k^{2}-1=0$，由$\Delta=8k^{4}-4(k^{2}+1)(2k^{2}-1)=4 - 4k^{2}＞0$，解得$-1＜k＜1$，则$x_{1}+x_{2}=\frac{2\sqrt{2}k^{2}}{k^{2}+1}$，$y_{1}+y_{2}=k(x_{1}+x_{2}-2\sqrt{2})=-\frac{2\sqrt{2}k}{k^{2}+1}$，所以$D(\frac{\sqrt{2}k^{2}}{k^{2}+1},-\frac{\sqrt{2}k}{k^{2}+1})$。
于是$\overrightarrow{PA}=(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2})$，$\overrightarrow{PD}=(\frac{\sqrt{2}}{k^{2}+1},-\frac{\sqrt{2}k}{k^{2}+1})$，所以$\overrightarrow{PA}·\overrightarrow{PD}=\frac{1 - k}{k^{2}+1}$。设$t=1 - k$，则$0＜t＜2$，$\overrightarrow{PA}·\overrightarrow{PD}=\frac{t}{(1 - t)^{2}+1}=\frac{t}{t^{2}-2t+2}=\frac{1}{t+\frac{2}{t}-2}\leq\frac{1}{2\sqrt{2}-2}=\frac{1}{2}+\frac{\sqrt{2}}{2}$，当且仅当$t=\sqrt{2}$，即$k=1-\sqrt{2}$时等号成立，故选A。