《2026年学易优高考二轮总复习数学》

(2)(2025·河南部分学校模拟)如图 1 所示，宫灯又称宫廷花灯，是中国彩灯中富有特色的汉民族传统手工艺品之一。图 2 是小明为自家设计的一个花灯的直观图，该花灯由上面的正六棱台与下面的正六棱柱组成，若正六棱台的上、下两个底面的边长分别为 $4\ dm$ 和 $2\ dm$，正六棱台与正六棱柱的高分别为 $1\ dm$ 和 $6\ dm$，则该花灯的表面积为(A)


A.$(108 + 30\sqrt{3})\ dm^2$
B.$(72 + 30\sqrt{3})\ dm^2$
C.$(64 + 24\sqrt{3})\ dm^2$
D.$(48 + 24\sqrt{3})\ dm^2$

答案：
(2)A　因为正六棱台的上、下两个底面的边长分别为4dm和2dm，正六棱台的高为1dm.所以正六棱台的斜高为$\sqrt{1^{2}+(4× \frac{\sqrt{3}}{2}-2× \frac{\sqrt{3}}{2})^{2}} = 2$dm，所以该花灯的表面积为$\frac{1}{2}×(4 + 2)× 2× 6+6× 2× 6+\frac{\sqrt{3}}{4}× 4^{2}× 6+\frac{\sqrt{3}}{4}× 2^{2}× 6 = 108 + 30\sqrt{3}(dm^{2})$.故选A.

训练 1 (1)“李白斗酒诗百篇，长安市上酒家眠”，本诗句中的“斗”的本义是指盛酒的器具，后又作为计量粮食的工具，某数学兴趣小组利用相关材料制作了一个如图所示的正四棱台来模拟“斗”，用它研究“斗”的相关几何性质，已知该四棱台的上、下底的边长分别是 $2$、$4$，高为 $1$，则该四棱台的表面积为(C)

A.$12\sqrt{2}$
B.$32$
C.$20 + 12\sqrt{2}$
D.$20 + 12\sqrt{3}$

答案：
(1)C　根据题意可知，该四棱台的侧面都是上底边长为2，下底边长为4的等腰梯形，所以侧面的斜高为$h'=\sqrt{1 + 1}=\sqrt{2}$，则一个侧面的面积为$(2 + 4)× \sqrt{2}× \frac{1}{2}=3\sqrt{2}$，上下底底面面积分别为$2× 2 = 4$，$4× 4 = 16$，所以该四棱台的表面积为$4 + 16 + 3\sqrt{2}× 4 = 20 + 12\sqrt{2}$.

(2)(2025·佛山二模)某圆锥高为 $\sqrt{3}$，母线与底面所成的角为 $\frac{\pi}{3}$，则该圆锥的表面积为(A)

A.$3\pi$
B.$4\pi$
C.$5\pi$
D.$6\pi$

答案：
(2)A　由圆锥高为$\sqrt{3}$，母线与底面所成的角为$\frac{\pi}{3}$，得圆锥底面圆半径$r = \frac{\sqrt{3}}{\tan\frac{\pi}{3}} = 1$，母线$l=\sqrt{1^{2}+(\sqrt{3})^{2}} = 2$，所以圆锥的表面积$S=\pi r^{2}+\pi rl = 3\pi$.

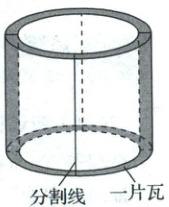
例 2 (1)(2025·北京东城区模拟)《天工开物》是我国明代科学家宋应星所著的一部综合性科学技术著作，书中记载了一种制造瓦片的方法。某校高一年级计划实践这种方法，为同学们准备了制瓦用的黏土和圆柱形的木质圆桶，圆桶底面外圆的直径为 $20\ cm$，高为 $20\ cm$。首先，在圆桶的外侧面均匀包上一层厚度为 $2\ cm$ 的黏土，然后，沿圆桶母线方向将黏土层分割成四等份(如图)，等黏土干后，即可得到大小相同的四片瓦。每位同学制作四片瓦，全年级共 $500$ 人，需要准备的黏土量(不计损耗)与下列哪个数字最接近。(参考数据：$\pi\approx 3.14$)(B)


A.$0.8\ m^3$
B.$1.4\ m^3$
C.$1.8\ m^3$
D.$2.2\ m^3$

答案：
(1)B　由条件可得四片瓦的体积$V=\pi× 12^{2}× 20-\pi× 10^{2}× 20 = 880\pi(cm^{3})$，所以500名学生，每人制作4片瓦共需黏土的体积为$500× 880\pi = 440000\pi(cm^{3})$，又$\pi\approx 3.14$，所以共需黏土的体积约为$1.3816m^{3}$，故选B.

(2)(2025·西安二模)在正四棱台 $A_1B_1C_1D_1 - ABCD$ 中，$AB = 2A_1B_1$，且三棱锥 $B_1 - ABC$ 的体积为 $6$，则该正四棱台的体积为(B)


A.$14$
B.$21$
C.$24$
D.$36$

答案：
(2)B　设正四棱台的高为$h(h\gt0)$，$AB = 2A_{1}B_{1}=2a$，则$V_{B_{1}-ABC}=\frac{1}{3}× \frac{1}{2}×(2a)^{2}× h=\frac{2}{3}a^{2}h = 6$，所以$a^{2}h = 9$，所以该正四棱台的体积为$\frac{1}{3}h(a^{2}+a× 2a + 4a^{2})=\frac{7}{3}a^{2}h = 21$.

例 3 (2025·河南 TOP20 名校联考)如图是一个水平放置在某地的三棱台型集雨器，已知上、下底的面积分别为 $4\ cm^2$ 和 $9\ cm^2$，高为 $3\ cm$。现在收集到的雨水平面与上、下底面的距离相等，则该地的降雨量为$\frac{455}{16}$$mm$。(降雨量等于集雨器中积水体积除以集雨器口的面积)

答案：
$\frac{455}{16}$　如图所示，将三棱台补成三棱锥$O - A_{1}B_{1}C_{1}$，

设三棱锥$O - ABC$的高为h，则$\frac{h}{h + 3}=\sqrt{\frac{4}{9}}$，解得$h = 6cm$，
所以三棱锥$O - ABC$的体积为$\frac{1}{3}× 4× 6 = 8(cm^{3})$，
再设$O - A_{0}B_{0}C_{0},O - A_{1}B_{1}C_{1}$的体积分别为$V_{0},V_{1}$，则$\frac{8}{V_{0}}=(\frac{h}{h+\frac{3}{2}})^{3}$，所以$\frac{8}{V_{0}}=(\frac{6}{6+\frac{3}{2}})^{3}$
所以$V_{0}=\frac{125}{8}cm^{3}$，同理$\frac{8}{V_{1}}=(\frac{6}{6 + 3})^{3}$
所以$V_{1}=(\frac{3}{2})^{3}× 8 = 27(cm^{3})$，
所以该地的降雨量为$\frac{V_{1}-V_{0}}{4}=\frac{91}{32}(cm)=\frac{455}{16}(mm)$.