2026年学易优高考二轮总复习数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优高考二轮总复习数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
(1)(2025·湖南郴州三模)已知椭圆 $ C:\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1(a>b>0) $ 的左、右焦点分别为 $ F_{1} $,$ F_{2} $,点 $ P $ 在椭圆 $ C $ 上,若 $ |PF_{1}|+|PF_{2}|=4 $,椭圆 $ C $ 的离心率为 $ \dfrac{1}{2} $,则椭圆 $ C $ 的焦距为(
A.1
B.2
C.$ \sqrt{3} $
D.$ 2\sqrt{3} $
B
)A.1
B.2
C.$ \sqrt{3} $
D.$ 2\sqrt{3} $
答案:
(1)B 依题意$\frac{c}{a} = \frac{1}{2}$,解得$a = 2$,$c = 1$,
所以焦距$2c = 2$。故选 B。
(1)B 依题意$\frac{c}{a} = \frac{1}{2}$,解得$a = 2$,$c = 1$,
所以焦距$2c = 2$。故选 B。
(2)(2025·重庆三模)双曲线 $ \dfrac{x^{2}}{8}-\dfrac{y^{2}}{b^{2}}=1(b>0) $ 的左、右焦点分别是 $ F_{1} $,$ F_{2} $,过 $ F_{2} $ 向双曲线的一条渐近线作垂线,垂足为 $ M $,若 $ \triangle F_{1}MF_{2} $ 的面积为 16,则双曲线的离心率为(
A.$ \sqrt{5} $
B.$ \sqrt{2} $
C.2
D.$ \sqrt{3} $
A
)A.$ \sqrt{5} $
B.$ \sqrt{2} $
C.2
D.$ \sqrt{3} $
答案:
(2)A 取渐近线方程为$y = \frac{b}{a}x$,由题意可得$F_{2}(c,0)$,所以垂线方程为$y = -\frac{a}{b}(x - c)$,联立两方程解得$x = \frac{a^{2}c}{a^{2}+b^{2}}$,$y = \frac{abc}{a^{2}+b^{2}}$,即$M$的坐标,因为$\triangle F_{1}MF_{2}$的面积为$16$,所以$\frac{1}{2}×2c×\frac{abc}{a^{2}+b^{2}} = 16$,又$c^{2}=a^{2}+b^{2}$,所以$2\sqrt{2}b = 16\Rightarrow b = 4\sqrt{2}$,$c^{2}=40$,所以离心率$e = \frac{c}{a} = \sqrt{5}$。故选 A。
(2)A 取渐近线方程为$y = \frac{b}{a}x$,由题意可得$F_{2}(c,0)$,所以垂线方程为$y = -\frac{a}{b}(x - c)$,联立两方程解得$x = \frac{a^{2}c}{a^{2}+b^{2}}$,$y = \frac{abc}{a^{2}+b^{2}}$,即$M$的坐标,因为$\triangle F_{1}MF_{2}$的面积为$16$,所以$\frac{1}{2}×2c×\frac{abc}{a^{2}+b^{2}} = 16$,又$c^{2}=a^{2}+b^{2}$,所以$2\sqrt{2}b = 16\Rightarrow b = 4\sqrt{2}$,$c^{2}=40$,所以离心率$e = \frac{c}{a} = \sqrt{5}$。故选 A。
(1)(2025·四川攀枝花三模)已知椭圆 $ C:\dfrac{x^{2}}{a^{2}}+\dfrac{y^{2}}{b^{2}}=1(a>b>0) $ 的上顶点为 $ A $,左、右焦点分别为 $ F_{1} $,$ F_{2} $,连接 $ AF_{2} $ 并延长交椭圆 $ C $ 于另一点 $ B $,若 $ |F_{1}B|:|AB|=4:5 $,则椭圆 $ C $ 的离心率为(
A.$ \dfrac{\sqrt{3}}{3} $
B.$ \dfrac{\sqrt{5}}{5} $
C.$ \dfrac{\sqrt{7}}{7} $
D.$ \dfrac{1}{3} $
B
)A.$ \dfrac{\sqrt{3}}{3} $
B.$ \dfrac{\sqrt{5}}{5} $
C.$ \dfrac{\sqrt{7}}{7} $
D.$ \dfrac{1}{3} $
答案:
(1)B 由图可知$|AF_{2}| = a$,
$|BF_{1}| + |BF_{2}| = 2a$,
根据$|F_{1}B|:|AB| = 4:5$,可设$|F_{1}B| = 4m$,$|AB| = 5m$,

则$4m + 5m - a = 2a\Rightarrow m = \frac{a}{3}$,所以$|F_{1}B| = \frac{4a}{3}$,$|AB| = \frac{5a}{3}$,$|F_{2}B| = \frac{2a}{3}$,
由三角形$BF_{1}F_{2}$中余弦定理得:$\frac{16a^{2}}{9}=4c^{2}+\frac{4a^{2}}{9}-2×2c×\frac{2a}{3}\cos\angle F_{1}F_{2}B$,
根据直角三角形$AOF_{2}$有:$\cos\angle F_{1}F_{2}B = -\cos\angle AF_{2}O = -\frac{c}{a}$,
代入上式可得:$\frac{16a^{2}}{9}=4c^{2}+\frac{4a^{2}}{9}+2×2c×\frac{2a}{3}×\frac{c}{a}\Rightarrow\frac{4a^{2}}{3}=\frac{20c^{2}}{3}\Rightarrow\frac{c^{2}}{a^{2}}=\frac{1}{5}\Rightarrow e = \frac{\sqrt{5}}{5}$。故选 B。
(1)B 由图可知$|AF_{2}| = a$,
$|BF_{1}| + |BF_{2}| = 2a$,
根据$|F_{1}B|:|AB| = 4:5$,可设$|F_{1}B| = 4m$,$|AB| = 5m$,

则$4m + 5m - a = 2a\Rightarrow m = \frac{a}{3}$,所以$|F_{1}B| = \frac{4a}{3}$,$|AB| = \frac{5a}{3}$,$|F_{2}B| = \frac{2a}{3}$,
由三角形$BF_{1}F_{2}$中余弦定理得:$\frac{16a^{2}}{9}=4c^{2}+\frac{4a^{2}}{9}-2×2c×\frac{2a}{3}\cos\angle F_{1}F_{2}B$,
根据直角三角形$AOF_{2}$有:$\cos\angle F_{1}F_{2}B = -\cos\angle AF_{2}O = -\frac{c}{a}$,
代入上式可得:$\frac{16a^{2}}{9}=4c^{2}+\frac{4a^{2}}{9}+2×2c×\frac{2a}{3}×\frac{c}{a}\Rightarrow\frac{4a^{2}}{3}=\frac{20c^{2}}{3}\Rightarrow\frac{c^{2}}{a^{2}}=\frac{1}{5}\Rightarrow e = \frac{\sqrt{5}}{5}$。故选 B。
(2)(多选)(2025·江苏苏州三模)某数学兴趣小组研究发现,在平面直角坐标系 $ xOy $ 中,反比例函数 $ y=\dfrac{1}{x} $ 的图象是双曲线 $ C $,记其焦点分别为 $ M $、$ N $,若 $ P $ 为其图象上任意一点,则(
A.$ y $ 轴是 $ C $ 的一条渐近线
B.点 $ (1,1) $ 是 $ C $ 的一个焦点
C.$ ||PM|-|PN||=2\sqrt{2} $
D.$ C $ 的离心率为 $ \sqrt{2} $
ACD
)A.$ y $ 轴是 $ C $ 的一条渐近线
B.点 $ (1,1) $ 是 $ C $ 的一个焦点
C.$ ||PM|-|PN||=2\sqrt{2} $
D.$ C $ 的离心率为 $ \sqrt{2} $
答案:
(2)ACD 反比例函数$y = \frac{1}{x}$的两条渐近线为$x$轴和$y$轴,A 对;
反比例函数$y = \frac{1}{x}$的两条渐近线垂直,故双曲线$C$为等轴双曲线,
因此,双曲线$C$的离心率为$\sqrt{2}$,D 对;
反比例函数$y = \frac{1}{x}$的图象分布在第一、三象限,且第一、三象限的角平分线方程为$y = x$,
联立$\begin{cases}y = \frac{1}{x}\\y = x\end{cases}$,解得$\begin{cases}x = 1\\y = 1\end{cases}$,或$\begin{cases}x = -1\\y = -1\end{cases}$,
所以,双曲线$C$的一个顶点为$(1,1)$,B 错;
双曲线$C$的实半轴长为$a = \sqrt{(0 - 1)^{2}+(0 - 1)^{2}} = \sqrt{2}$,
故$||PM| - |PN|| = 2a = 2\sqrt{2}$,C 对。故选 ACD。
(2)ACD 反比例函数$y = \frac{1}{x}$的两条渐近线为$x$轴和$y$轴,A 对;
反比例函数$y = \frac{1}{x}$的两条渐近线垂直,故双曲线$C$为等轴双曲线,
因此,双曲线$C$的离心率为$\sqrt{2}$,D 对;
反比例函数$y = \frac{1}{x}$的图象分布在第一、三象限,且第一、三象限的角平分线方程为$y = x$,
联立$\begin{cases}y = \frac{1}{x}\\y = x\end{cases}$,解得$\begin{cases}x = 1\\y = 1\end{cases}$,或$\begin{cases}x = -1\\y = -1\end{cases}$,
所以,双曲线$C$的一个顶点为$(1,1)$,B 错;
双曲线$C$的实半轴长为$a = \sqrt{(0 - 1)^{2}+(0 - 1)^{2}} = \sqrt{2}$,
故$||PM| - |PN|| = 2a = 2\sqrt{2}$,C 对。故选 ACD。
(1)(2025·北京海淀三模)点 $ M(5,3) $ 到抛物线 $ y = ax^{2}(a\neq0) $ 的准线的距离为 6,那么该抛物线的标准方程是(
A.$ x^{2}=12y $
B.$ x^{2}=\dfrac{1}{12}y $ 或 $ x^{2}=-\dfrac{1}{36}y $
C.$ x^{2}=-\dfrac{1}{36}y $
D.$ x^{2}=12y $ 或 $ x^{2}=-36y $
D
)A.$ x^{2}=12y $
B.$ x^{2}=\dfrac{1}{12}y $ 或 $ x^{2}=-\dfrac{1}{36}y $
C.$ x^{2}=-\dfrac{1}{36}y $
D.$ x^{2}=12y $ 或 $ x^{2}=-36y $
答案:
(1)D 将$y = ax^{2}$转化为$x^{2}=\frac{1}{a}y$,
当$a > 0$时,抛物线开口向上,准线方程$y = -\frac{1}{4a}$,
点$M(5,3)$到准线的距离为$3+\frac{1}{4a}=6$,解得$a = \frac{1}{12}$,
所以抛物线方程为$y = \frac{1}{12}x^{2}$,即$x^{2}=12y$;
当$a < 0$时,抛物线开口向下,准线方程$y = -\frac{1}{4a}$,
点$M(5,3)$到准线的距离为$|3+\frac{1}{4a}| = 6$,解得$a = -\frac{1}{36}$或$a = \frac{1}{12}$(舍去),
所以抛物线方程为$y = -\frac{1}{36}x^{2}$,即$x^{2}=-36y$。
所以抛物线的方程为$x^{2}=12y$或$x^{2}=-36y$。故选 D。
(1)D 将$y = ax^{2}$转化为$x^{2}=\frac{1}{a}y$,
当$a > 0$时,抛物线开口向上,准线方程$y = -\frac{1}{4a}$,
点$M(5,3)$到准线的距离为$3+\frac{1}{4a}=6$,解得$a = \frac{1}{12}$,
所以抛物线方程为$y = \frac{1}{12}x^{2}$,即$x^{2}=12y$;
当$a < 0$时,抛物线开口向下,准线方程$y = -\frac{1}{4a}$,
点$M(5,3)$到准线的距离为$|3+\frac{1}{4a}| = 6$,解得$a = -\frac{1}{36}$或$a = \frac{1}{12}$(舍去),
所以抛物线方程为$y = -\frac{1}{36}x^{2}$,即$x^{2}=-36y$。
所以抛物线的方程为$x^{2}=12y$或$x^{2}=-36y$。故选 D。
(2)(多选)(2025·甘肃白银三模)已知 $ P(a,b) $,$ Q(c,1) $ 为抛物线 $ C:x^{2}=2py(p>0) $ 上两点,$ C $ 的焦点为 $ F $,且 $ |QF|=3 $,$ A(2,1) $,则下列结论正确的是(
A.$ C $ 的准线为 $ l:x=-2 $
B.当 $ a = 4 $ 时,$ |PF| $ 的值为 5
C.$ |PA|+|PF| $ 的最小值为 3
D.$ |PA|-|PF| $ 的最大值为 $ \sqrt{5} $
CD
)A.$ C $ 的准线为 $ l:x=-2 $
B.当 $ a = 4 $ 时,$ |PF| $ 的值为 5
C.$ |PA|+|PF| $ 的最小值为 3
D.$ |PA|-|PF| $ 的最大值为 $ \sqrt{5} $
答案:
(2)CD 因为$Q(c,1)$,$|QF| = 3$,$F(0,\frac{p}{2})$,准线方程为$y = -\frac{p}{2}$,
所以由抛物线的定义可得$1+\frac{1}{2}p = 3\Rightarrow p = 4$,
$C$的准线为$y = -2$,故选项 A 错误;
当$a = 4$时,$b = 2$,$|PF|$的值为$b+\frac{1}{2}p = 2 + 2 = 4$,故选项 B 错误;
如图,过点$P$作$PB\perp$准线于点$B$,则由抛物线定义可知:$|PF| = |PB|$,则$|PA| + |PF| = |PA| + |PB|$,当$A$、$P$、$B$三点共线时,和最小,最小值为$1 + 2 = 3$,C 正确;

由题意得:$F(0,2)$,连接$AF$并延长,交抛物线于点$P$,此点即为$|PA| - |PF|$取最大值的点,此时$|PA| - |PF| = |AF| = \sqrt{4 + 1} = \sqrt{5}$,其他位置的点$P'$,由三角形两边之差小于第三边得:$|P'A| - |P'F| < |AF| = \sqrt{5}$,故$|PA| - |PF|$的最大值为$\sqrt{5}$,D 正确。故选 CD。
(2)CD 因为$Q(c,1)$,$|QF| = 3$,$F(0,\frac{p}{2})$,准线方程为$y = -\frac{p}{2}$,
所以由抛物线的定义可得$1+\frac{1}{2}p = 3\Rightarrow p = 4$,
$C$的准线为$y = -2$,故选项 A 错误;
当$a = 4$时,$b = 2$,$|PF|$的值为$b+\frac{1}{2}p = 2 + 2 = 4$,故选项 B 错误;
如图,过点$P$作$PB\perp$准线于点$B$,则由抛物线定义可知:$|PF| = |PB|$,则$|PA| + |PF| = |PA| + |PB|$,当$A$、$P$、$B$三点共线时,和最小,最小值为$1 + 2 = 3$,C 正确;

由题意得:$F(0,2)$,连接$AF$并延长,交抛物线于点$P$,此点即为$|PA| - |PF|$取最大值的点,此时$|PA| - |PF| = |AF| = \sqrt{4 + 1} = \sqrt{5}$,其他位置的点$P'$,由三角形两边之差小于第三边得:$|P'A| - |P'F| < |AF| = \sqrt{5}$,故$|PA| - |PF|$的最大值为$\sqrt{5}$,D 正确。故选 CD。
(1)苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑(如图 1 所示),“门”的内侧曲线呈抛物线形。图 2 是“东方之门”的示意图,已知 $ |CD|=30\ m $,$ |AB|=60\ m $,点 $ D $ 到直线 $ AB $ 的距离为 $ 150\ m $,则此抛物线顶端 $ O $ 到 $ AB $ 的距离为(
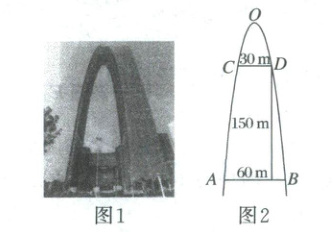
A.$ 180\ m $
B.$ 200\ m $
C.$ 220\ m $
D.$ 240\ m $
B
)
A.$ 180\ m $
B.$ 200\ m $
C.$ 220\ m $
D.$ 240\ m $
答案:
(1)B 以$O$为坐标原点,建立如图所示的平面直角坐标系,设抛物线的方程为$x^{2}=-2py(p > 0)$,由题意设$D(15,h)$,$h < 0$,$B(30,h - 150)$,
则$\begin{cases}15^{2}=-2ph\\30^{2}=-2p(h - 150)\end{cases}$,
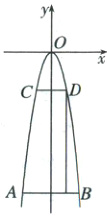
解得$\begin{cases}h = -50\\p = 2.25\end{cases}$,
所以此抛物线顶端$O$到$AB$的距离为$50 + 150 = 200(m)$。
(1)B 以$O$为坐标原点,建立如图所示的平面直角坐标系,设抛物线的方程为$x^{2}=-2py(p > 0)$,由题意设$D(15,h)$,$h < 0$,$B(30,h - 150)$,
则$\begin{cases}15^{2}=-2ph\\30^{2}=-2p(h - 150)\end{cases}$,

解得$\begin{cases}h = -50\\p = 2.25\end{cases}$,
所以此抛物线顶端$O$到$AB$的距离为$50 + 150 = 200(m)$。
(2)焦点为 $ F $ 的抛物线 $ y^{2}=2px(p>0) $ 上有一点 $ P(2,2p) $,$ O $ 为坐标原点,则满足 $ |MP|=|MO|=|MF| $ 的点 $ M $ 的坐标为(
A.$ \left(\dfrac{1}{2},\dfrac{3}{2}\right) $
B.$ \left(\dfrac{1}{4},\dfrac{7}{4}\right) $
C.$ \left(\dfrac{1}{2},\dfrac{5}{2}\right) $
D.$ \left(\dfrac{1}{4},\dfrac{9}{4}\right) $
B
)A.$ \left(\dfrac{1}{2},\dfrac{3}{2}\right) $
B.$ \left(\dfrac{1}{4},\dfrac{7}{4}\right) $
C.$ \left(\dfrac{1}{2},\dfrac{5}{2}\right) $
D.$ \left(\dfrac{1}{4},\dfrac{9}{4}\right) $
答案:
(2)B 将点$P$的坐标代入抛物线中得$(2p)^{2}=2p×2$,解得$p = 1$,则$P(2,2)$,所以$OP$的斜率为$1$,且$OP$的中点为$(1,1)$,
则$OP$的垂直平分线方程为$y - 1 = -(x - 1)$,
即$x + y - 2 = 0$,
又$OF$的垂直平分线方程为$x = \frac{1}{4}$,
$|MP| = |MO| = |MF|$,则点$M$为$OP$的垂直平分线和$OF$的垂直平分线的交点,
所以点$M$的坐标为$(\frac{1}{4},\frac{7}{4})$。
(2)B 将点$P$的坐标代入抛物线中得$(2p)^{2}=2p×2$,解得$p = 1$,则$P(2,2)$,所以$OP$的斜率为$1$,且$OP$的中点为$(1,1)$,
则$OP$的垂直平分线方程为$y - 1 = -(x - 1)$,
即$x + y - 2 = 0$,
又$OF$的垂直平分线方程为$x = \frac{1}{4}$,
$|MP| = |MO| = |MF|$,则点$M$为$OP$的垂直平分线和$OF$的垂直平分线的交点,
所以点$M$的坐标为$(\frac{1}{4},\frac{7}{4})$。
查看更多完整答案,请扫码查看


