《2026年学易优高考二轮总复习数学》

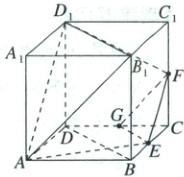
(2)(多选)(2025·黄山模拟)如图，已知正方体ABCD-A₁B₁C₁D₁，点E，F，G分别为棱BC，CC₁，CD的中点，下列结论正确的有(AB)


A.AE与D₁F共面
B.平面AB₁D₁//平面GFE
C.AE⊥EF
D.BF//平面AB₁D₁

答案：

(2)AB 如图所示，对于A，在正方体$ABCD - A_1B_1C_1D_1$中，点$E$，$F$，$G$分别为棱$BC$，$CC_1$，$CD$的中点，连接$BC_1$，所以$EF // BC_1$，而$BC_1 // AD_1$，所以$EF // AD_1$，所以$AE$与$D_1F$共面，A正确；
对于B，因为$BB_1 // DD_1$且$BB_1 = DD_1$，所以四边形$BB_1D_1D$为平行四边形，则$BD // B_1D_1$，又因为$E$，$G$分别为$BC$，$CD$的中点，所以$EG // BD$，所以$EG // B_1D_1$，又由A选项分析知$EF // AD_1$，因为$EF \cap EG = E$，$EF$，$EG \subset$平面$EFG$，$B_1D_1 \cap AD_1 = D_1$，$B_1D_1$，$AD_1 \subset$平面$AB_1D_1$，所以平面$EFG //$平面$AB_1D_1$，B正确；对于C，因为$EF // AD_1$且$EF \neq AD_1$，即四边形$AD_1FE$为等腰梯形，故$AE$，$EF$不垂直，C错误；对于D，由B选项的分析，平面$EFG //$平面$AB_1D_1$，而$BF \cap$平面$EFG = F$，所以$BF$与平面$AB_1D_1$不平行，D错误。

(1)已知直线l，m，n是三条不同的直线，α，β为两个不同的平面，则下列说法正确的是(D)

A.若l//m，l//n，m⊂α，n⊂α，则l//α
B.若m//α，m//n，则n//α
C.若l⊥α，l//m，α⊥β，则m//β
D.若α⊥β，α∩β=m，l⊂α，l⊥m，则l⊥β

答案：
(1)D　若$l // m$，$l // n$，$m \subset \alpha$，$n \subset \alpha$，则$l // \alpha$或$l \subset \alpha$，故选项A不正确；若$m // \alpha$，$m // n$，则$n // \alpha$或$n \subset \alpha$，故选项B不正确；若$l \perp \alpha$，$l // m$，$\alpha \perp \beta$，则$m // \beta$或$m \subset \beta$，故选项C不正确；由面面垂直的性质定理可知选项D正确。故选D。

(2)(2025·武汉质检)已知四棱锥P-ABCD，平面PAD⊥平面ABCD，四边形ABCD是正方形，E为PC中点，则(C)

A.BE//平面PAD
B.PD⊥平面ABCD
C.平面PAB⊥平面PAD
D.DE=EB

答案：
(2)C　易知$BC //$平面$PAD$，因为$BE \cap BC = B$，且两条直线都在平面$PBC$内，所以$BE$不可能平行平面$PAD$，故A错误；
举反例，如图，$PH$垂直平面$ABCD$时，由于$PD \cap PH = P$，所以$PD$不垂直于平面$ABCD$，故B错误；因为平面$PAD \perp$平面$ABCD$且平面$PAD \cap$平面$ABCD = AD$，$AB \perp AD$，所以$AB \perp$平面$PAD$，因为$AB \subset$平面$PAB$，所以平面$PAB \perp$平面$PAD$，故C正确；没有任何条件可以证明$DE = EB$，故D错误。故选C。

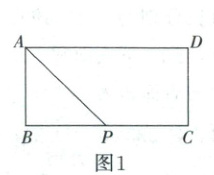
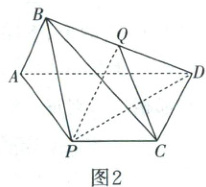
(2025·陕西汉中模拟预测)如图1，在矩形ABCD中，AD=2AB=2，P是BC的中点，连接AP，将△PAB沿直线AP翻折，使得平面PAB⊥平面APCD(如图2)，连接BC，BD，Q是棱BD的中点。
(1)证明：AB⊥平面PBD；
(2)证明：CQ//平面PAB。

答案：
证明：
(1)因为在矩形$ABCD$中，$AD = 2AB = 2$，$P$是$BC$的中点，
所以$AP = PD = \sqrt{2}$，即$AP^2 + PD^2 = AD^2$，所以$PD \perp AP$，
又因为平面$PAB \perp$平面$APCD$，平面$PAB \cap$平面$APCD = PA$，$PA \subset$平面$APCD$，
所以$PD \perp$平面$PAB$，
又因为$AB \subset$平面$PAB$，又因为$AB \perp BP$，$PB \cap PD = P$，$PB$，$PD \subset$平面$PBD$，所以$AB \perp$平面$PBD$；
(2)如图所示，取$AD$中点$E$，连接$QE$，$CE$，
因为在矩形$ABCD$中，$AD = 2AB = 2$，$P$是$BC$的中点，
所以$AE // PC$，$AE = PC$，即四边形$AECP$为平行四边形，

从而$AP // CE$，又因为$CE \not\subset$平面$PAB$，$AP \subset$平面$PAB$，
所以$CE //$平面$PAB$，
又因为$Q$，$E$分别是$DB$，$DA$的中点，
所以$QE // AB$，
又因为$QE \not\subset$平面$PAB$，$AB \subset$平面$PAB$，
所以$QE //$平面$PAB$，
又因为$QE \cap EC = E$，$QE$，$EC \subset$平面$QEC$，
所以平面$QEC //$平面$PAB$，
又因为$CQ \subset$平面$QEC$，所以$CQ //$平面$PAB$。

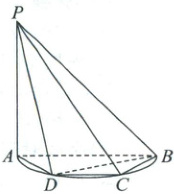
(2025·甘肃金昌模拟预测)如图，在四棱锥P-ABCD中，PA⊥平面ABD，PA=AB=4，C，D是平面ABCD内以AB为直径的半圆上的两点，且AD=2，DC//AB。
(1)证明：BD⊥平面PAD；
(2)证明：平面PAD⊥平面PBD。

答案： 证明：
(1)因为$PA \perp$平面$ABD$，$BD \subset$平面$ABD$，所以$PA \perp BD$。
因为$D$是以$AB$为直径的半圆上的一点，所以$AD \perp BD$，
因为$PA$，$AD \subset$平面$PAD$，$PA \cap AD = A$，所以$BD \perp$平面$PAD$。
(2)因为$BD \subset$平面$PBD$，由
(1)得$BD \perp$平面$PAD$，
所以平面$PAD \perp$平面$PBD$。