《2026年学易优高考二轮总复习数学》

训练2 (2025·重庆诊断)当前，新一轮科技革命和产业变革蓬勃兴起，以区块链为代表的新一代信息技术迅猛发展，现收集某地近 6 年区块链企业总数量相关数据，如表：

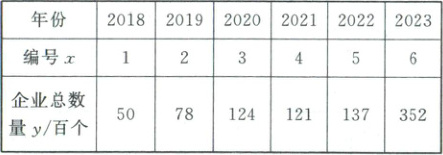
(1)若用模型 $y = a e^{bx}$拟合 $y$ 与 $x$ 的关系，根据提供的数据，求出 $y$ 与 $x$ 的经验回归方程；
(2)为了促进公司间的合作与发展，区块链联合总部决定进行一次信息化技术比赛，邀请甲、乙、丙三家区块链公司参赛.比赛规则如下：
①每场比赛有两个公司参加，并决出胜负；②每场比赛获胜的公司与未参加此场比赛的公司进行下一场的比赛；③在比赛中，若有一个公司首先获胜两场，则本次比赛结束，该公司获得此次信息化技术比赛的“优胜公司”称号.已知在每场比赛中，甲胜乙的概率为$\frac{1}{2}$，甲胜丙的概率为$\frac{1}{3}$，乙胜丙的概率为$\frac{3}{5}$，若首场由甲乙比赛，求甲公司获得“优胜公司”称号的概率.
参考数据：$\sum_{i = 1}^{6}u_{i} = 28.5,\sum_{i = 1}^{6}x_{i}u_{i} = 106.05$，其中，$u_{i} = \ln y_{i}$.
参考公式：对于一组数据$(x_{i},y_{i})(i = 1,2,3,·s,n)$，其经验回归方程$\hat{y} = \hat{b}x + \hat{a}$的斜率和截距的最小二乘估计分别为$\hat{b} = \frac{\sum_{i = 1}^{n}x_{i}y_{i} - n\bar{x}· \bar{y}}{\sum_{i = 1}^{n}x_{i}^{2} - n\bar{x}^{2}}$，$\hat{a} = \bar{y} - \hat{b}\bar{x}$.

答案： 训练2 解：
(1)令$\hat{u}=\ln\hat{y}=\ln(a\mathrm{e}^{bx})=\hat{b}x+\ln\hat{a}$，$\overline{x}=\frac{1 + 2 + 3 + 4 + 5 + 6}{6}=3.5$，$\overline{u}=\frac{28.5}{6}=4.75$，则$\hat{b}=\frac{\sum_{i = 1}^{6}x_iu_i - n\overline{x}·\overline{u}}{\sum_{i = 1}^{6}x_{i}^{2}-n\overline{x}^2}=\frac{106.05 - 6×3.5×4.75}{1^2 + 2^2 + 3^2 + 4^2 + 5^2 + 6^2 - 6×3.5^2}=0.36$，
$\ln\hat{a}=4.75 - 0.36×3.5 = 3.49$，所以$\hat{a}=\mathrm{e}^{3.49}$，
所以$y$关于$x$的经验回归方程为$y=\mathrm{e}^{3.49}·\mathrm{e}^{0.36x}=\mathrm{e}^{0.36x + 3.49}$．
(2)设甲公司获得“优胜公司”称号为事件A，
则$P(A)=\frac{1}{2}×\frac{1}{3}+\frac{1}{2}×\frac{2}{3}×\frac{3}{5}×\frac{1}{2}+\frac{1}{2}×\frac{2}{5}×\frac{1}{3}×\frac{1}{2}×\frac{1}{2}×\frac{1}{3}=\frac{3}{10}$．
所以甲公司获得“优胜公司”称号的概率为$\frac{3}{10}$．

例4 (2024·全国甲卷)某工厂进行生产线智能化升级改造.升级改造后，从该工厂甲、乙两个车间的产品中随机抽取 150 件进行检验，数据如下：

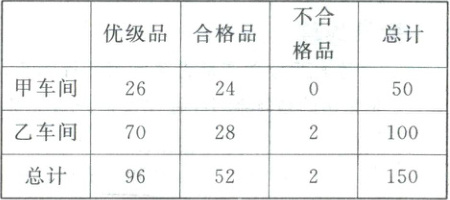
(1)填写如下列联表：

能否有 95％的把握认为甲、乙两车间产品的优级品率存在差异？能否有 99％的把握认为甲、乙两车间产品的优级品率存在差异？
(2)已知升级改造前该工厂产品的优级品率 $p = 0.5$.设$\bar{p}$为升级改造后抽取的 $n$ 件产品的优级品率.如果$\bar{p} ＞ p + 1.65\sqrt{\frac{p(1 - p)}{n}}$，则认为该工厂产品的优级品率提高了.根据抽取的 150 件产品的数据，能否认为生产线智能化升级改造后，该工厂产品的优级品率提高了？$(\sqrt{150} \approx 12.247)$
附:$\chi ^{2} = \frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)},n = a + b + c + d$.

答案：
【例4】 解：
(1)第1步：填写列联表
填写如下列联表：

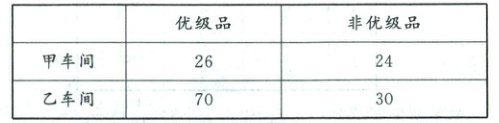
第2步：作出完整的$2×2$列联表
则完整的$2×2$列联表如下：

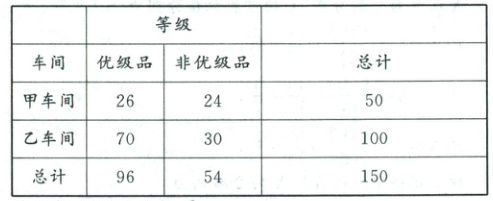
第3步：根据公式求$\chi^2$
$\chi^2=\frac{150×(26×30 - 70×24)^2}{96×54×50×100}=4.6875$．
第4步：根据$\chi^2$的值判断
因为$\chi^2 = 4.6875＞3.841$，所以有95%的把握认为甲、乙两车间产品的优级品率存在差异；
因为$\chi^2 = 4.6875＜6.635$，所以没有99%的把握认为甲、乙两车间产品的优级品率存在差异．
(2)第1步：求出$\overline{p}$
由题意可知$\overline{p}=\frac{96}{150}=0.64$，
第2步：求出$p + 1.65\sqrt{\frac{p(1 - p)}{n}}$的值
又$p + 1.65\sqrt{\frac{p(1 - p)}{n}}=0.5 + 1.65×\sqrt{\frac{0.5×(1 - 0.5)}{150}}\approx0.5 + 1.65×\frac{0.5}{12.247}\approx0.57$，
第3步：由$\overline{p}$与$p + 1.65\sqrt{\frac{p(1 - p)}{n}}$的大小关系判断
所以$\overline{p}＞p + 1.65\sqrt{\frac{p(1 - p)}{n}}$，所以能认为生产线智能化升级改造后，该工厂产品的优级品率提高了．