2026年学易优高考二轮总复习数学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优高考二轮总复习数学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
例 4 (2025·成都诊断)在四棱锥 $P - ABCD$ 中,底面 $ABCD$ 是边长为 $4$ 的正方形,$\angle PBA = \angle PBC$,$PD\perp AD$,$Q$ 为正方形 $ABCD$ 内一动点(不含边界),且满足 $QA\perp QP$,若 $PD = 2$,则三棱锥 $Q - PBC$ 的体积的最小值为(
A.$3$
B.$\frac{8}{3}$
C.$\frac{4}{3}$
D.$2$
B
)A.$3$
B.$\frac{8}{3}$
C.$\frac{4}{3}$
D.$2$
答案:
B 如图,因为$\angle PBA=\angle PBC$,$AB = CB$,$PB = PB$,
所以$\triangle PAB\cong\triangle PCB$,所以$PA = PC$,
又$AD = CD$,$PD = PD$,所以$\triangle PAD\cong\triangle PCD$,所以$\angle PDC=\angle PDA$,
因为$PD\perp AD$,所以$PD\perp CD$.
又$AD\cap CD = D$,$AD,CD\subset$平面$ABCD$,
所以$PD\perp$平面$ABCD$.
连接$QD$,因为$AQC$平面$ABCD$,
所以$PD\perp AQ$,
又$QA\perp QP,QP\cap PD = P$,$QP,PD\subset$平面$PDQ$,所以$AQ\perp$平面$PDQ$,
又$QDC$平面$PDQ$,所以$AQ\perp QD$,
故点$Q$在以$AD$为直径的半圆上(不包含$A,D$两点).
又$V_{Q - PBC}=V_{P - QBC}=\frac{1}{3}S_{\triangle QBC}· PD$,
所以当$S_{\triangle QBC}$最小,即点$Q$到$BC$的距离最小,即点$Q$是半圆弧$AD$的中点时,三棱锥$Q - PBC$的体积最小,
故三棱锥$Q - PBC$的体积的最小值为$\frac{1}{3}× \frac{1}{2}× 4× 2× 2=\frac{8}{3}$.故选B.
所以$\triangle PAB\cong\triangle PCB$,所以$PA = PC$,
又$AD = CD$,$PD = PD$,所以$\triangle PAD\cong\triangle PCD$,所以$\angle PDC=\angle PDA$,
因为$PD\perp AD$,所以$PD\perp CD$.
又$AD\cap CD = D$,$AD,CD\subset$平面$ABCD$,
所以$PD\perp$平面$ABCD$.
连接$QD$,因为$AQC$平面$ABCD$,
所以$PD\perp AQ$,
又$QA\perp QP,QP\cap PD = P$,$QP,PD\subset$平面$PDQ$,所以$AQ\perp$平面$PDQ$,
又$QDC$平面$PDQ$,所以$AQ\perp QD$,
故点$Q$在以$AD$为直径的半圆上(不包含$A,D$两点).
又$V_{Q - PBC}=V_{P - QBC}=\frac{1}{3}S_{\triangle QBC}· PD$,
所以当$S_{\triangle QBC}$最小,即点$Q$到$BC$的距离最小,即点$Q$是半圆弧$AD$的中点时,三棱锥$Q - PBC$的体积最小,
故三棱锥$Q - PBC$的体积的最小值为$\frac{1}{3}× \frac{1}{2}× 4× 2× 2=\frac{8}{3}$.故选B.
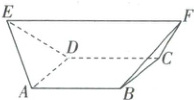
训练 2 (1)(2025·北京大兴三模)《九章算术》是我国古代的一部数学名著,书中记载了一类名为“羡除”的五面体。如图,在羡除 $ABCDEF$ 中,底面 $ABCD$ 是正方形,$EF//$ 平面 $ABCD$,$EF = 2$,其余棱长都为 $1$,则这个几何体的体积为(
A.$2\sqrt{2}$
B.$\sqrt{2}$
C.$\frac{2\sqrt{2}}{3}$
D.$\frac{\sqrt{2}}{3}$
D
)
A.$2\sqrt{2}$
B.$\sqrt{2}$
C.$\frac{2\sqrt{2}}{3}$
D.$\frac{\sqrt{2}}{3}$
答案:
(1)D 连接$AC,BD$交于点$M$,取$EF$的中点为$O$,则$OM\perp$平面$ABCD$,
由$EF = 2$,其余棱长都为1,所以$OM=\frac{\sqrt{2}}{2}$.
取$BC$的中点为$G$,连接$FG$,则$FG\perp BC$,过$O$作$ON\perp FG$,
则$ON\perp$平面$BCF$,如图所示,
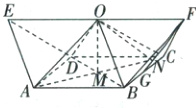
由题意可知,$FG=\frac{\sqrt{3}}{2}$,则$FN=\frac{\sqrt{3}}{2}× \frac{2}{3}=\frac{\sqrt{3}}{3}$,所以$OG=\sqrt{OF^{2}-FN^{2}}=\frac{\sqrt{6}}{3}$,
所以$V=\frac{1}{3}× 1× 1× \frac{\sqrt{2}}{2}+2× \frac{1}{3}× \frac{\sqrt{3}}{4}× 1^{2}× \frac{\sqrt{6}}{3}=\frac{\sqrt{2}}{3}$.故选D.
(1)D 连接$AC,BD$交于点$M$,取$EF$的中点为$O$,则$OM\perp$平面$ABCD$,
由$EF = 2$,其余棱长都为1,所以$OM=\frac{\sqrt{2}}{2}$.
取$BC$的中点为$G$,连接$FG$,则$FG\perp BC$,过$O$作$ON\perp FG$,
则$ON\perp$平面$BCF$,如图所示,

由题意可知,$FG=\frac{\sqrt{3}}{2}$,则$FN=\frac{\sqrt{3}}{2}× \frac{2}{3}=\frac{\sqrt{3}}{3}$,所以$OG=\sqrt{OF^{2}-FN^{2}}=\frac{\sqrt{6}}{3}$,
所以$V=\frac{1}{3}× 1× 1× \frac{\sqrt{2}}{2}+2× \frac{1}{3}× \frac{\sqrt{3}}{4}× 1^{2}× \frac{\sqrt{6}}{3}=\frac{\sqrt{2}}{3}$.故选D.
(2)紫砂壶是中国特有的手工制造陶土工艺品,其制作始于明朝正德年间。紫砂壶的壶型众多,经典的有西施壶、掇球壶、石瓢壶、潘壶等。其中石瓢壶的壶体可以近似看成一个圆台,如图给出了一个石瓢壶的相关数据(单位:$cm$),现在向这个空石瓢壶中加入 $91\pi\ cm^3$ 的矿泉水后,问石瓢壶内水深为

A.$2.8$
B.$2.9$
C.$3$
D.$3.1$
3
$cm$(C
)
A.$2.8$
B.$2.9$
C.$3$
D.$3.1$
答案:
(2)C 由题知矿泉水的体积为$91\pi cm^{3}$,将圆台的中轴面拿出,补全为一个三角形,如图所示.
加入矿泉水后,记石瓢壶内水深为$h$,水平面半径为$r$,
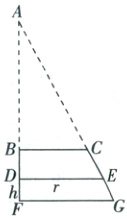
由图可知$\triangle ABC\sim\triangle AFG$,所以$\frac{AB}{AF}=\frac{BC}{FG}$,
即$\frac{AB}{AB + 6}=\frac{2}{3}$,解得$AB = 12$.
由$\triangle ABC\sim\triangle ADE$,得$\frac{AB}{AD}=\frac{BC}{DE}$,即$\frac{12}{18 - h}=\frac{4}{r}$,解得$h = 18 - 3r$.
故加入矿泉水后圆台的体积为$V=\frac{1}{3}\pi(18 - 3r)(6^{2}+6r + r^{2}) = 91\pi$,
解得$r=\sqrt[3]{125}=5$,所以$h = 18 - 3r = 3$.
(2)C 由题知矿泉水的体积为$91\pi cm^{3}$,将圆台的中轴面拿出,补全为一个三角形,如图所示.
加入矿泉水后,记石瓢壶内水深为$h$,水平面半径为$r$,

由图可知$\triangle ABC\sim\triangle AFG$,所以$\frac{AB}{AF}=\frac{BC}{FG}$,
即$\frac{AB}{AB + 6}=\frac{2}{3}$,解得$AB = 12$.
由$\triangle ABC\sim\triangle ADE$,得$\frac{AB}{AD}=\frac{BC}{DE}$,即$\frac{12}{18 - h}=\frac{4}{r}$,解得$h = 18 - 3r$.
故加入矿泉水后圆台的体积为$V=\frac{1}{3}\pi(18 - 3r)(6^{2}+6r + r^{2}) = 91\pi$,
解得$r=\sqrt[3]{125}=5$,所以$h = 18 - 3r = 3$.
1. (2022·新高考Ⅱ卷)已知正三棱台的高为1,上、下底面边长分别为$3\sqrt{3}$和$4\sqrt{3}$,其顶点都在同一球面上,则该球的表面积为(
A.$100\pi$
B.$128\pi$
C.$144\pi$
D.$192\pi$
A
)A.$100\pi$
B.$128\pi$
C.$144\pi$
D.$192\pi$
答案:
1.A 设正三棱台上下底面所在圆面的半径分别为$r_1$,$r_2$,所以$2r_1=\frac{3\sqrt{3}}{\sin60°}$,$2r_2=\frac{4\sqrt{3}}{\sin60°}$,即$r_1=3$,$r_2=4$。设球心到上下底面的距离分别为$d_1$,$d_2$,球的半径为$R$,所以$d_1=\sqrt{R^2 - 9}$,$d_2=\sqrt{R^2 - 16}$。故$\vert d_1 - d_2\vert = 1$或$d_1 + d_2 = 1$,即$\vert\sqrt{R^2 - 9} - \sqrt{R^2 - 16}\vert = 1$或$\sqrt{R^2 - 9} + \sqrt{R^2 - 16} = 1$,解得$R^2 = 25$符合题意,所以球的表面积为$S = 4\pi R^2 = 100\pi$。
2. (2022·全国乙卷)已知球$O$的半径为1,四棱锥的顶点为$O$,底面的四个顶点均在球$O$的球面上,则当该四棱锥的体积最大时,其高为(
A.$\frac{1}{3}$
B.$\frac{1}{2}$
C.$\frac{\sqrt{3}}{3}$
D.$\frac{\sqrt{2}}{2}$
C
)A.$\frac{1}{3}$
B.$\frac{1}{2}$
C.$\frac{\sqrt{3}}{3}$
D.$\frac{\sqrt{2}}{2}$
答案:
2.C 设该四棱锥底面为四边形$ABCD$,高为$h$,四边形$ABCD$所在小圆半径为$r$。设四边形$ABCD$对角线夹角为$\alpha$,则$S_{ABCD}=\frac{1}{2}· AC· BD·\sin\alpha\leqslant\frac{1}{2}· AC· BD\leqslant\frac{1}{2}· 2r· 2r = 2r^2$(当且仅当四边形$ABCD$为正方形时等号成立),即当四棱锥的顶点$O$到底面$ABCD$所在小圆距离一定时,底面$ABCD$面积最大值为$2r^2$。又$r^2 + h^2 = 1$,则$V_{O - ABCD}=\frac{1}{3}· 2r^2· h=\frac{\sqrt{2}}{3}\sqrt{r^2· r^2· 2h^2}\leqslant\frac{\sqrt{2}}{3}\sqrt{(\frac{r^2 + r^2 + 2h^2}{3})^3}=\frac{4\sqrt{3}}{27}$,当且仅当$r^2 = 2h^2$即$h=\frac{\sqrt{3}}{3}$时等号成立。故选C。
3. (2023·全国甲卷)在正方体$ABCD - A_1B_1C_1D_1$中,$E,F$分别为$AB,C_1D_1$的中点.以$EF$为直径的球的球面与该正方体的棱共有
12
个公共点.
答案:
3.12 如图,线段$EF$过正方体的中心,所以以$EF$为直径的球的球心即正方体的中心,球的半径为$\frac{EF}{2}$,而正方体的中心到每一条棱的距离均为$\frac{EF}{2}$,所以以$EF$为直径的球与每一条棱均相切,所以共有12个公共点。

3.12 如图,线段$EF$过正方体的中心,所以以$EF$为直径的球的球心即正方体的中心,球的半径为$\frac{EF}{2}$,而正方体的中心到每一条棱的距离均为$\frac{EF}{2}$,所以以$EF$为直径的球与每一条棱均相切,所以共有12个公共点。

4. (2025·全国二卷)一个底面半径为$4$cm,高为$9$cm的封闭圆柱形容器(容器壁厚度忽略不计)内有两个半径相等的铁球,则铁球半径的最大值为cm.
答案:
2.5 设铁球半径为$r\mathrm{cm}$,若两个铁球的球心在竖直方向 上,且分别与两个底面相切,则铁球球心与圆柱上、下底面 的距离均为$r$,此时铁球的半径为$\frac{9}{4}\mathrm{cm}$. 当两球球心不在竖直方向上时,设两个铁球的球心分别为 $O_1$,$O_2$,此种情况下,当铁球半径最大时,如图1所示,圆柱 与两铁球的轴截面如图2所示,其中$ABCD$为圆柱的轴截 面,$O_2P\perp AB$,$O_1P\perp AD$,则有$O_2P=9-2r$,$O_1P=8-2r$, $O_1O_2=2r$,则有$(2r)^2=(8-2r)^2+(9-2r)^2$,即$4r^2-$ $68r+145=0$, 即$(2r-29)(2r-5)=0$,解得$r_1=14.5$(舍去),$r_2=2.5$.
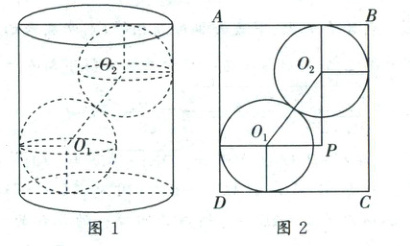
因为$2.5>\frac{9}{4}=2.25$,所以铁球半径的最大值为$2.5\mathrm{cm}$.
2.5 设铁球半径为$r\mathrm{cm}$,若两个铁球的球心在竖直方向 上,且分别与两个底面相切,则铁球球心与圆柱上、下底面 的距离均为$r$,此时铁球的半径为$\frac{9}{4}\mathrm{cm}$. 当两球球心不在竖直方向上时,设两个铁球的球心分别为 $O_1$,$O_2$,此种情况下,当铁球半径最大时,如图1所示,圆柱 与两铁球的轴截面如图2所示,其中$ABCD$为圆柱的轴截 面,$O_2P\perp AB$,$O_1P\perp AD$,则有$O_2P=9-2r$,$O_1P=8-2r$, $O_1O_2=2r$,则有$(2r)^2=(8-2r)^2+(9-2r)^2$,即$4r^2-$ $68r+145=0$, 即$(2r-29)(2r-5)=0$,解得$r_1=14.5$(舍去),$r_2=2.5$.

因为$2.5>\frac{9}{4}=2.25$,所以铁球半径的最大值为$2.5\mathrm{cm}$.
查看更多完整答案,请扫码查看


