第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
19. (8 分)【实践探究】
(1)如图 1,在 $\triangle ABC$ 中,$\angle A = 50^{\circ}$,$\angle ABC$ 的平分线与外角 $\angle ACD$ 的平分线相交于点 $E$,则 $\angle E = $
【拓展延伸】
(3)
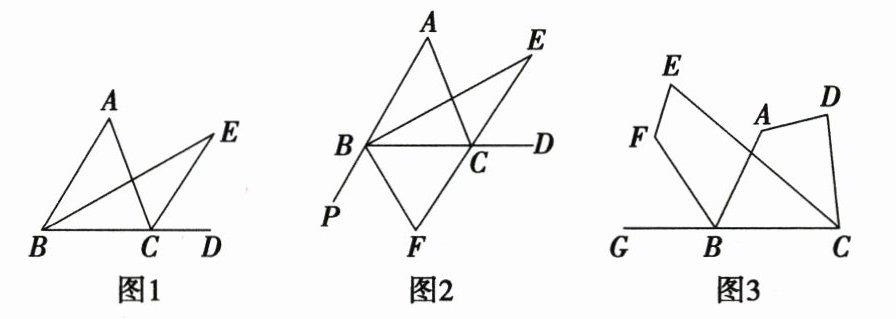
(1)如图 1,在 $\triangle ABC$ 中,$\angle A = 50^{\circ}$,$\angle ABC$ 的平分线与外角 $\angle ACD$ 的平分线相交于点 $E$,则 $\angle E = $
25°
;【拓展延伸】
(3)
195°
如图 3,已知四边形 $ABCD$,$CE$ 为 $\angle BCD$ 的平分线,$BF$ 是外角 $\angle ABG$ 的平分线,连接 $EF$。已知 $\angle A = 130^{\circ}$,$\angle D = 80^{\circ}$。请直接写出 $\angle E + \angle F$ 的度数。
答案:
(1)由条件可知∠EBD=1/2∠ABC,∠ECD=1/2∠ACD。
∵∠A=50°,
∴∠ACD−∠ABC=∠A=50°。
∴∠E=∠ECD−∠EBD
=1/2∠ACD−1/2∠ABC
=1/2×50°
=25°。
故答案为:25°。
(2)由条件可知∠EBD=1/2∠ABC,∠FBD=1/2∠CBP。
∴∠EBF=∠EBD+∠FBD=1/2∠ABC+1/2∠CBP=1/2(∠ABC+∠CBP)=90°。
由
(1)可得∠E=25°,
∴∠F=180°−∠EBF−∠E=65°。
(3)由条件可知∠BCD+∠ABC=360°−130°−80°=150°。
∵CE为∠BCD的平分线,BF是外角∠ABG的平分线,
∴∠BCE=1/2∠BCD,∠ABF=1/2∠ABG。
∴∠E+∠F=360°−∠BCE−∠ABF−∠ABC
=360°−1/2∠BCD−1/2∠ABG−∠ABC
=360°−1/2(∠BCD+∠ABC)−1/2(∠ABG+∠ABC)
=360°−1/2×150°−1/2×180°
=195°。
(1)由条件可知∠EBD=1/2∠ABC,∠ECD=1/2∠ACD。
∵∠A=50°,
∴∠ACD−∠ABC=∠A=50°。
∴∠E=∠ECD−∠EBD
=1/2∠ACD−1/2∠ABC
=1/2×50°
=25°。
故答案为:25°。
(2)由条件可知∠EBD=1/2∠ABC,∠FBD=1/2∠CBP。
∴∠EBF=∠EBD+∠FBD=1/2∠ABC+1/2∠CBP=1/2(∠ABC+∠CBP)=90°。
由
(1)可得∠E=25°,
∴∠F=180°−∠EBF−∠E=65°。
(3)由条件可知∠BCD+∠ABC=360°−130°−80°=150°。
∵CE为∠BCD的平分线,BF是外角∠ABG的平分线,
∴∠BCE=1/2∠BCD,∠ABF=1/2∠ABG。
∴∠E+∠F=360°−∠BCE−∠ABF−∠ABC
=360°−1/2∠BCD−1/2∠ABG−∠ABC
=360°−1/2(∠BCD+∠ABC)−1/2(∠ABG+∠ABC)
=360°−1/2×150°−1/2×180°
=195°。
20. (8 分)如图,在 $\triangle ABC$ 中,$AB = AC$,$BE \perp AC$ 于点 $E$,且 $D$,$E$ 分别是 $AB$,$AC$ 的中点,延长 $BC$ 至点 $F$,使 $CF = CE$。
(1)求 $\angle ABC$ 的度数;
(2)求证:$BE = FE$。
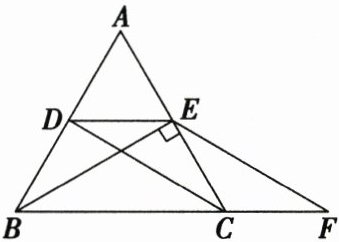
(1)求 $\angle ABC$ 的度数;
(2)求证:$BE = FE$。

答案:
(1)
∵BE⊥AC于点E,E是AC的中点,
∴AB=BC。
∵AB=AC,
∴△ABC是等边三角形。
∴∠ABC=60°。
(2)证明:
∵CF=CE,
∴∠F=∠CEF。
∵∠ACB=∠F+∠CEF=60°,
∴∠F=30°。
∵△ABC是等边三角形,BE⊥AC,
∴∠EBC=1/2∠ABC=1/2×60°=30°。
∴∠F=∠EBC。
∴BE=FE。
(1)
∵BE⊥AC于点E,E是AC的中点,
∴AB=BC。
∵AB=AC,
∴△ABC是等边三角形。
∴∠ABC=60°。
(2)证明:
∵CF=CE,
∴∠F=∠CEF。
∵∠ACB=∠F+∠CEF=60°,
∴∠F=30°。
∵△ABC是等边三角形,BE⊥AC,
∴∠EBC=1/2∠ABC=1/2×60°=30°。
∴∠F=∠EBC。
∴BE=FE。
查看更多完整答案,请扫码查看


