第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
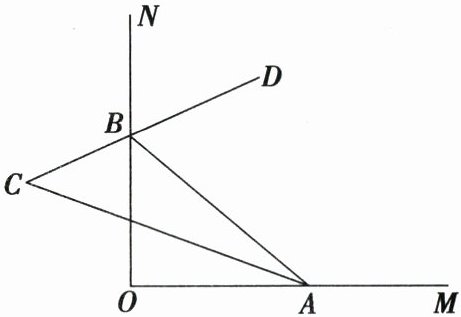
22. (10分)如图,已知$\angle MON = 90^{\circ}$,点$A$,$B分别在射线OM$,$ON$上,$\angle OAB的平分线与\angle ABN的平分线所在的直线交于点C$.
(1)求$\angle C$的度数;
(2)当点$A$,$B分别在射线OM$,$ON$上移动时,试问$\angle C$的大小是否发生变化. 若保持不变,请说明理由;若发生变化,请求出变化范围.
(1)求$\angle C$的度数;
(2)当点$A$,$B分别在射线OM$,$ON$上移动时,试问$\angle C$的大小是否发生变化. 若保持不变,请说明理由;若发生变化,请求出变化范围.

答案:
解:
(1)
∵AC平分∠OAB,
∴∠OAB=2∠BAC.
∵BD平分∠ABN,
∴∠ABN=2∠ABD.
∵∠ABD=∠C+∠BAC,
∴2∠ABD=2∠C+2∠BAC.
∴∠ABN=2∠C+∠OAB.
∵∠ABN=∠O+∠OAB=90°+∠OAB,
∴2∠C+∠OAB=90°+∠OAB.
∴∠C=45°.
(2)∠C的大小不变,推导过程同
(1).
(1)
∵AC平分∠OAB,
∴∠OAB=2∠BAC.
∵BD平分∠ABN,
∴∠ABN=2∠ABD.
∵∠ABD=∠C+∠BAC,
∴2∠ABD=2∠C+2∠BAC.
∴∠ABN=2∠C+∠OAB.
∵∠ABN=∠O+∠OAB=90°+∠OAB,
∴2∠C+∠OAB=90°+∠OAB.
∴∠C=45°.
(2)∠C的大小不变,推导过程同
(1).
23. (11分)阅读与思考
下面是博学小组研究性学习报告的部分内容. 请认真阅读并完成相应的任务.
```关于“正多角星图形”的研究报告(博学小组)
研究对象:正多角星图形.
研究思路:类比一般图形,按“概念—性质—判定”的路径,由一般到特殊进行研究.
研究方法:观察(测量、实验)—猜想—推理证明.
教材知识:
①三角形的内角和为▲______.
②三角形的一个外角等于与它两个不相邻的内角的 ■______.
研究内容:
【一般概念】正多角星图形是一种特殊的几何图形,它由等长的直线段(边)连接而成,形成一个具有多个等大的尖角(顶点)的闭合多边形.
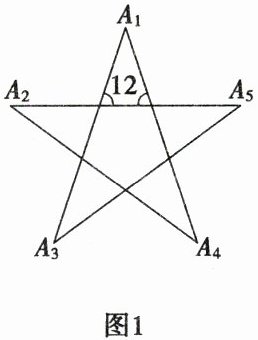
【特例研究】由正多角星图形的定义,对于五角星图形研究,可得结论:$\angle A_1+\angle A_2+\angle A_3+\angle A_4+\angle A_5= 180^{\circ}$,
证明:如图1,由三角形外角的性质,可得$\angle1= \angle A_3+\angle A_5$,
```
任务:
(1)材料中,“▲”处内容为______,“■”处的内容为______;
(2)补全材料中……“”处的证明过程;
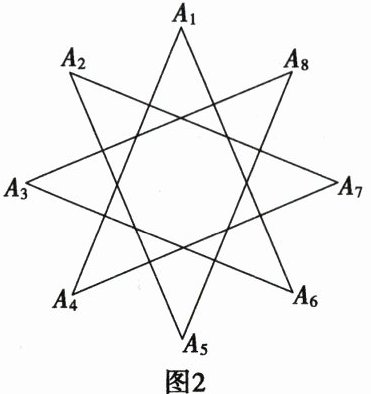
(3)由以上材料内容,可知图2中正八角星八个尖角的度数和为______.
下面是博学小组研究性学习报告的部分内容. 请认真阅读并完成相应的任务.
```关于“正多角星图形”的研究报告(博学小组)
研究对象:正多角星图形.
研究思路:类比一般图形,按“概念—性质—判定”的路径,由一般到特殊进行研究.
研究方法:观察(测量、实验)—猜想—推理证明.
教材知识:
①三角形的内角和为▲______.
②三角形的一个外角等于与它两个不相邻的内角的 ■______.
研究内容:
【一般概念】正多角星图形是一种特殊的几何图形,它由等长的直线段(边)连接而成,形成一个具有多个等大的尖角(顶点)的闭合多边形.
【特例研究】由正多角星图形的定义,对于五角星图形研究,可得结论:$\angle A_1+\angle A_2+\angle A_3+\angle A_4+\angle A_5= 180^{\circ}$,
证明:如图1,由三角形外角的性质,可得$\angle1= \angle A_3+\angle A_5$,
```

任务:
(1)材料中,“▲”处内容为______,“■”处的内容为______;
(2)补全材料中……“”处的证明过程;
(3)由以上材料内容,可知图2中正八角星八个尖角的度数和为______.

答案:
解:
(1)三角形的内角和为180°;三角形的一个外角等于与它两个不相邻的内角的和;故答案为:180°,和.
(2)证明:
∵∠1=∠A3+∠A5,∠2=∠A2+∠A4,∠A1+∠1+∠2=180°,
∴∠A1+∠A2+∠A3+∠A4+∠A5=180°.
(3)如图2,


∵∠1=180°−(∠A4+∠A7),∠2=180°−(∠A2+∠A5),∠3=180°−(∠A3+∠A8),∠4=180°−(∠A1+∠A6),
又
∵∠1+∠2+∠3+∠4=360°,
∴∠1+∠2+∠3+∠4=4×180°−(∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7+∠A8)=360°,
∴∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7+∠A8=360°.故答案为:360°.
解:
(1)三角形的内角和为180°;三角形的一个外角等于与它两个不相邻的内角的和;故答案为:180°,和.
(2)证明:
∵∠1=∠A3+∠A5,∠2=∠A2+∠A4,∠A1+∠1+∠2=180°,
∴∠A1+∠A2+∠A3+∠A4+∠A5=180°.
(3)如图2,


∵∠1=180°−(∠A4+∠A7),∠2=180°−(∠A2+∠A5),∠3=180°−(∠A3+∠A8),∠4=180°−(∠A1+∠A6),
又
∵∠1+∠2+∠3+∠4=360°,
∴∠1+∠2+∠3+∠4=4×180°−(∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7+∠A8)=360°,
∴∠A1+∠A2+∠A3+∠A4+∠A5+∠A6+∠A7+∠A8=360°.故答案为:360°.
查看更多完整答案,请扫码查看


