《2025年核心素养学练评八年级数学上册人教版》

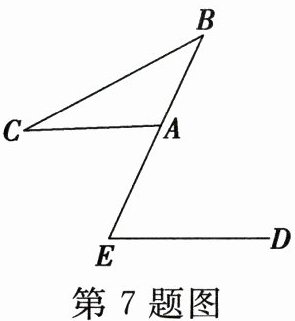
7. 如图,已知 $ AC // ED $,$ \angle C = 26^{\circ} $,$ \angle B = 37^{\circ} $,则 $ \angle E $ 的度数是(A)

∵∠C = 26°,∠B = 37°,∠CAE = ∠C + ∠B,∴∠CAE = 63°,又∵AC//ED,∴∠E = ∠CAE = 63°.故选A.
A.$ 63^{\circ} $
B.$ 83^{\circ} $
C.$ 73^{\circ} $
D.$ 53^{\circ} $

答案： A
∵∠C = 26°,∠B = 37°,∠CAE = ∠C + ∠B,
∴∠CAE = 63°,又
∵AC//ED,
∴∠E = ∠CAE = 63°.故选A.

8. 一个等腰三

角

形

的两边长分别为 4 和 8,则它的周长是( C)

A.$ 12 $
B.$ 16 $
C.$ 20 $
D.$ 16 $ 或 $ 20 $

答案： C　由题意，等腰三角形的三边长分别为4,4,8或4,8,8，根据三角形的三边关系可知，长分别为4,4,8的边不能构成三角形，所以等腰三角形的周长为4 + 8 + 8 = 20.故选C.

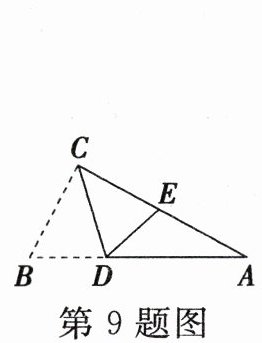
9. 如图,在 $ \triangle ABC $ 中,$ \angle ACB = 90^{\circ} $,沿 $ CD $ 折叠 $ \triangle CBD $,使点 $ B $ 恰好落在 $ AC $ 边上的点 $ E $ 处。若 $ \angle A = 24^{\circ} $,则 $ \angle EDC $ 的度数为(C)

A.$ 42^{\circ} $
B.$ 66^{\circ} $
C.$ 69^{\circ} $
D.$ 77^{\circ} $

答案： C　在△ABC中，
∵∠ACB = 90°,∠A = 24°,
∴∠B = 90° - ∠A = 66°.由折叠的性质知，∠CED = ∠B = 66°,∠DCE = $\frac{1}{2}$∠ACB = 45°.
∵∠EDC + ∠CED + ∠DCE = 180°,
∴∠EDC = 180° - ∠CED - ∠DCE = 69°.故选C.

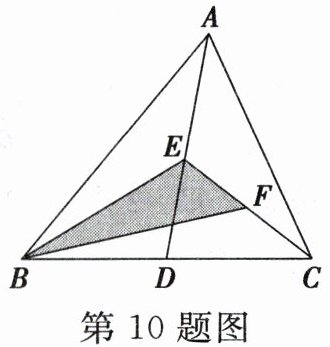
10. 如图,在 $ \triangle ABC $ 中,点 $ D $,$ E $,$ F $ 分别为边 $ BC $,$ AD $,$ CE $ 的中点,且 $ S_{\triangle ABC} = 4\ cm^2 $,则 $ S_{阴影} = $(B)

A.$ 2\ cm^2 $
B.$ 1\ cm^2 $
C.$ \frac{1}{2}\ cm^2 $
D.$ \frac{1}{4}\ cm^2 $

答案： B　由题意可知，S△ABD = S△ACD = $\frac{1}{2}$S△ABC = 2cm²,S△BDE = $\frac{1}{2}$S△ABD = 1cm²,S△CDE = $\frac{1}{2}$S△ACD = 1cm²,
∴S△BEC = S△BDE + S△CDE = 2cm²,
∴S阴影 = $\frac{1}{2}$S△BEC = 1cm².故选B.

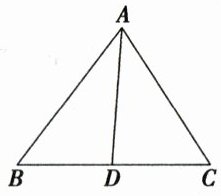
11. 如图,当 $ $BD$ = $CD$ $ 时,$ AD $ 是 $ \triangle ABC $ 的中线；当 $ $∠BAD$ = $∠CAD$ $ 时,$ AD $ 是 $ \triangle ABC $ 的角平分线。

答案： BD　CD　∠BAD　∠CAD　由中线和角平分线的定义可得.

12. 有下列事件：①人们通常会在栅栏门上斜着钉上一根木条；②新植的树木常用一些粗木与之成角度支撑起来防止倒斜；③四边形模具。其中应用了三角形稳定性的有 ①②(填序号)。

答案： ①②　四边形不具有稳定性.

13. 已知 $ \triangle ABC $ 的三个内角度数之比为 $ \angle A : \angle B : \angle C = 2 : 3 : 5 $,则 $ \angle B = $54°,$ \angle C = $90°。

答案： 54°　90°
∵∠A:∠B:∠C = 2:3:5,∠A + ∠B + ∠C = 180°,
∴∠B = $\frac{3}{2 + 3 + 5}$×180° = 54°,∠C = $\frac{5}{2 + 3 + 5}$×180° = 90°.

14. 若 $ \triangle ABC $ 三条边的长为 $ a $,$ b $,$ c $,且满足 $ |a - b| + (b - c)^2 = 0 $,则 $ \triangle ABC $ 是 $ $等边$ $ 三角形。

答案： 等边
∵|a - b|+(b - c)² = 0,
∴|a - b| = 0,(b - c)² = 0.
∴a = b,b = c.
∴a = b = c.
∴△ABC是等边三角形.

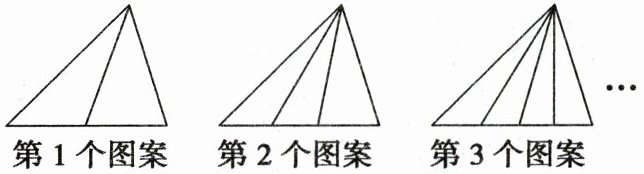
15. 观察如图所示的图案,它们是按照一定规律排列的,依照此规律,第 4 个图案中共有 $ $15$ $ 个三角形,第 10 个图案共有 $ $66$ $ 个三角形,第 $ n $ 个图案有 $ $$\frac{(n + 1)(n + 2)}{2}$$ $ 个三角形。

答案： 15　66　$\frac{(n + 1)(n + 2)}{2}$　第1个图案中三角形的个数:2 + 1 = 3(个),第2个图案中三角形的个数:3 + 2 + 1 = 6(个),第3个图案中三角形的个数:4 + 3 + 2 + 1 = $\frac{4×5}{2}$ = 10(个),第4个图案中三角形的个数:5 + 4 + 3 + 2 + 1 = $\frac{5×6}{2}$ = 15(个)，由此归纳第n个图形中三角形的个数:(n + 1)+n+(n - 1)+…+2 + 1 = $\frac{(n + 1)(n + 2)}{2}$个.