第91页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
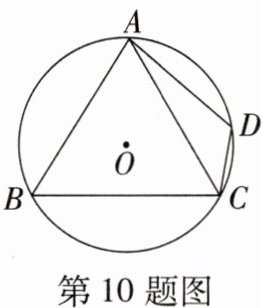
10. (2023·山东青岛中考)如图,四边形$ABCD是\odot O$的内接四边形,$\angle B = 58^{\circ}$,$\angle ACD = 40^{\circ}$。若$\odot O的半径为5$,则$\overset{\frown}{DC}$的长为 ( )
A.$\frac{13}{3}\pi$
B.$\frac{10}{9}\pi$
C.$\pi$
D.$\frac{1}{2}\pi$

A.$\frac{13}{3}\pi$
B.$\frac{10}{9}\pi$
C.$\pi$
D.$\frac{1}{2}\pi$
答案:
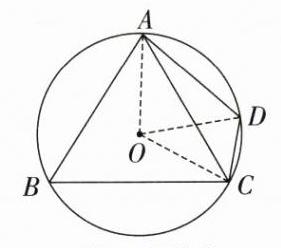
10.C[提示:如图,连接OA,OD,OC,
∵∠B=58°,∠ACD=40°,
∴∠AOC=2∠B=116°,∠AOD=2∠ACD=80°,
∴∠DOC=36°,
∴$\widehat{DC}$的长=$\frac{36π×5}{180}=π$.
10.C[提示:如图,连接OA,OD,OC,
∵∠B=58°,∠ACD=40°,
∴∠AOC=2∠B=116°,∠AOD=2∠ACD=80°,
∴∠DOC=36°,
∴$\widehat{DC}$的长=$\frac{36π×5}{180}=π$.

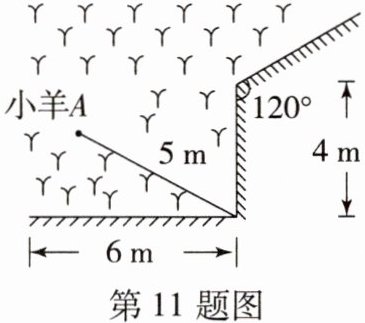
11. (情境题)如图,一根$5\mathrm{m}$长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊$A$(羊只能在草地上活动),那么小羊$A$在草地上的最大活动区域面积是 ( )
A.$\frac{17}{12}\pi\mathrm{m}^{2}$
B.$\frac{77}{12}\pi\mathrm{m}^{2}$
C.$\frac{25}{4}\pi\mathrm{m}^{2}$
D.$\frac{17}{6}\pi\mathrm{m}^{2}$

A.$\frac{17}{12}\pi\mathrm{m}^{2}$
B.$\frac{77}{12}\pi\mathrm{m}^{2}$
C.$\frac{25}{4}\pi\mathrm{m}^{2}$
D.$\frac{17}{6}\pi\mathrm{m}^{2}$
答案:
11.B[提示:如图,
∵大扇形的圆心角是90°,半径是5m,
∴大扇形面积=$\frac{90π×25}{360}=\frac{25}{4}π(m²)$.
∵小扇形的圆心角是180° - 120°=60°,半径是1m,
∴小扇形面积=$\frac{60π×1²}{360}=\frac{π}{6}(m²)$.
∴小羊A在草地上的最大活动区域面积=$\frac{25}{4}π+\frac{π}{6}=\frac{77}{12}π(m²)$.

11.B[提示:如图,
∵大扇形的圆心角是90°,半径是5m,
∴大扇形面积=$\frac{90π×25}{360}=\frac{25}{4}π(m²)$.
∵小扇形的圆心角是180° - 120°=60°,半径是1m,
∴小扇形面积=$\frac{60π×1²}{360}=\frac{π}{6}(m²)$.
∴小羊A在草地上的最大活动区域面积=$\frac{25}{4}π+\frac{π}{6}=\frac{77}{12}π(m²)$.

12. (2023·山东滨州中考)如图,某玩具品牌的标志由半径为$1\mathrm{cm}$的三个等圆构成,且三个等圆$\odot O_{1}$,$\odot O_{2}$,$\odot O_{3}$相互经过彼此的圆心,则图中三个阴影部分的面积之和为 ( )

A.$\frac{1}{4}\pi\mathrm{cm}^{2}$
B.$\frac{1}{3}\pi\mathrm{cm}^{2}$
C.$\frac{1}{2}\pi\mathrm{cm}^{2}$
D.$\pi\mathrm{cm}^{2}$

A.$\frac{1}{4}\pi\mathrm{cm}^{2}$
B.$\frac{1}{3}\pi\mathrm{cm}^{2}$
C.$\frac{1}{2}\pi\mathrm{cm}^{2}$
D.$\pi\mathrm{cm}^{2}$
答案:
12.C[提示:如图,连接$O_{1}A,O_{2}A,O_{1}B,O_{3}B,O_{2}C,O_{3}C,O_{1}O_{2},O_{1}O_{3},O_{2}O_{3}$,则$△O_{1}AO_{2},△O_{1}BO_{3},△O_{2}CO_{3},△O_{1}O_{2}O_{3}$是边长为1的正三角形,
∴$S_{阴影部分}=3S_{扇形O_{1}O_{2}A}=3×\frac{60π×1²}{360}=\frac{π}{2}(cm²)$.

12.C[提示:如图,连接$O_{1}A,O_{2}A,O_{1}B,O_{3}B,O_{2}C,O_{3}C,O_{1}O_{2},O_{1}O_{3},O_{2}O_{3}$,则$△O_{1}AO_{2},△O_{1}BO_{3},△O_{2}CO_{3},△O_{1}O_{2}O_{3}$是边长为1的正三角形,
∴$S_{阴影部分}=3S_{扇形O_{1}O_{2}A}=3×\frac{60π×1²}{360}=\frac{π}{2}(cm²)$.

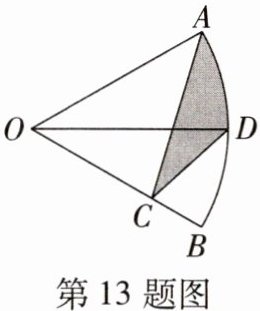
13. 如图,在扇形$AOB$中,$\angle AOB = 60^{\circ}$,$OD平分\angle AOB交\overset{\frown}{AB}于点D$,点$C是半径OB$上一动点,若$OA = 1$,则阴影部分周长的最小值为 ( )
A.$\sqrt{2}+\frac{\pi}{6}$
B.$\sqrt{2}+\frac{\pi}{3}$
C.$2\sqrt{2}+\frac{\pi}{6}$
D.$2\sqrt{2}+\frac{\pi}{3}$

A.$\sqrt{2}+\frac{\pi}{6}$
B.$\sqrt{2}+\frac{\pi}{3}$
C.$2\sqrt{2}+\frac{\pi}{6}$
D.$2\sqrt{2}+\frac{\pi}{3}$
答案:
13.A[提示:如图,作D点关于直线OB的对称点E,连接AE,与OB的交点为C点,此时阴影部分周长最小.在扇形AOB中,∠AOB=60°,OD平分∠AOB交$\widehat{AB}$于点D,
∴∠AOD=∠BOD=30°.由轴对称的性质得∠EOB=∠BOD=30°,OE=OD,
∴∠AOE=90°,
∴△AOE是等腰直角三角形.
∵OA=1,
∴AE=$\sqrt{2}$,$\widehat{AD}$的长=$\frac{30π×1}{180}=\frac{π}{6}$,
∴阴影部分周长的最小值为$\sqrt{2}+\frac{π}{6}$.

13.A[提示:如图,作D点关于直线OB的对称点E,连接AE,与OB的交点为C点,此时阴影部分周长最小.在扇形AOB中,∠AOB=60°,OD平分∠AOB交$\widehat{AB}$于点D,
∴∠AOD=∠BOD=30°.由轴对称的性质得∠EOB=∠BOD=30°,OE=OD,
∴∠AOE=90°,
∴△AOE是等腰直角三角形.
∵OA=1,
∴AE=$\sqrt{2}$,$\widehat{AD}$的长=$\frac{30π×1}{180}=\frac{π}{6}$,
∴阴影部分周长的最小值为$\sqrt{2}+\frac{π}{6}$.

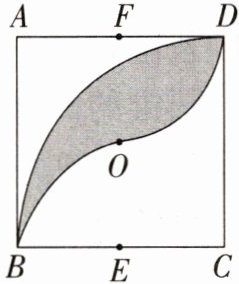
14. 如图,正方形$ABCD的边长为2$,$O$为对角线的交点,点$E$,$F分别为BC$,$AD$的中点。以$C$为圆心,$2为半径作圆弧BD$,再分别以$E$,$F$为圆心,$1为半径作圆弧BO$,$OD$,求图中阴影部分的面积。

答案:
14.解:连接BD,EF,如图,
∵正方形ABCD的边长为2,O为对角线的交点,
∴EF,BD经过点O,且EF⊥AD,EF⊥CB.
∵点E,F分别为BC,AD的中点,
∴FD=FO=EO=EB=1,
∴$\widehat{OB}=\widehat{OD}$,OB=OD.
∴弓形OB=弓形OD.
∴阴影部分的面积等于弓形BD的面积.
∴$S_{阴影}=S_{扇形CBD}-S_{△CBD}=\frac{90π×2²}{360}-\frac{1}{2}×2×2=π - 2$.

14.解:连接BD,EF,如图,
∵正方形ABCD的边长为2,O为对角线的交点,
∴EF,BD经过点O,且EF⊥AD,EF⊥CB.
∵点E,F分别为BC,AD的中点,
∴FD=FO=EO=EB=1,
∴$\widehat{OB}=\widehat{OD}$,OB=OD.
∴弓形OB=弓形OD.
∴阴影部分的面积等于弓形BD的面积.
∴$S_{阴影}=S_{扇形CBD}-S_{△CBD}=\frac{90π×2²}{360}-\frac{1}{2}×2×2=π - 2$.

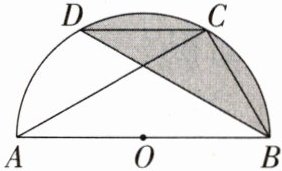
15. 如图,$C$,$D是以AB$为直径的半圆上的两点,$\angle CAB = \angle DBA$,连接$BC$,$CD$。
(1)求证:$CD// AB$;
(2)若$AB = 4$,$\angle ACD = 30^{\circ}$,求阴影部分的面积。
(1)求证:$CD// AB$;
(2)若$AB = 4$,$\angle ACD = 30^{\circ}$,求阴影部分的面积。

答案:
15.
(1)证明:
∵∠ACD=∠DBA,∠CAB=∠DBA,
∴∠CAB=∠ACD,
∴CD//AB.
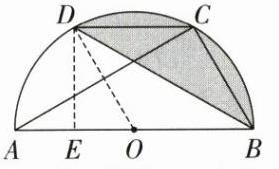
(2)解:如图,连接OD,过点D作DE⊥AB,垂足为E.
∵∠ACD=30°,
∴∠AOD=60°,
∴∠BOD=180° - ∠AOD =120°,
∴$S_{扇形BOD}=\frac{120π×2²}{360}=\frac{4π}{3}$.在Rt△ODE中,∠ODE =30°,OD=$\frac{1}{2}$AB=2,
∴OE=$\frac{1}{2}$OD=1,
∴DE=$\sqrt{OD² - OE²}=\sqrt{2² - 1²}=\sqrt{3}$,
∴$S_{△BOD}=\frac{1}{2}OB\cdot DE=\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$,
∴$S_{阴影}=S_{扇形BOD}-S_{△BOD}=\frac{4π}{3}-\sqrt{3}$.
15.
(1)证明:
∵∠ACD=∠DBA,∠CAB=∠DBA,
∴∠CAB=∠ACD,
∴CD//AB.
(2)解:如图,连接OD,过点D作DE⊥AB,垂足为E.
∵∠ACD=30°,
∴∠AOD=60°,
∴∠BOD=180° - ∠AOD =120°,
∴$S_{扇形BOD}=\frac{120π×2²}{360}=\frac{4π}{3}$.在Rt△ODE中,∠ODE =30°,OD=$\frac{1}{2}$AB=2,
∴OE=$\frac{1}{2}$OD=1,
∴DE=$\sqrt{OD² - OE²}=\sqrt{2² - 1²}=\sqrt{3}$,
∴$S_{△BOD}=\frac{1}{2}OB\cdot DE=\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$,
∴$S_{阴影}=S_{扇形BOD}-S_{△BOD}=\frac{4π}{3}-\sqrt{3}$.

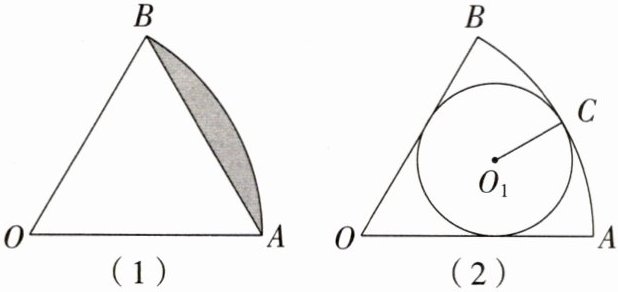
16. (素养题)如图(1),已知扇形$AOB$中,$\angle AOB = 60^{\circ}$,半径$R = 3$。
(1)求扇形$AOB的面积S及图中阴影部分的面积S_{阴}$;
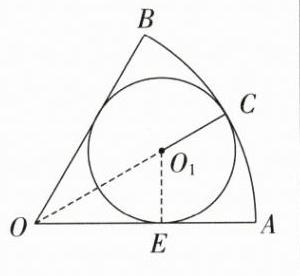
(2)如图(2)在扇形$AOB$的内部,$\odot O_{1}与OA$,$OB$都相切,且与$\overset{\frown}{AB}只有一个交点C$,此时我们称$\odot O_{1}为扇形AOB$的内切圆,试求$\odot O_{1}的面积S_{1}$。
(1)求扇形$AOB的面积S及图中阴影部分的面积S_{阴}$;
(2)如图(2)在扇形$AOB$的内部,$\odot O_{1}与OA$,$OB$都相切,且与$\overset{\frown}{AB}只有一个交点C$,此时我们称$\odot O_{1}为扇形AOB$的内切圆,试求$\odot O_{1}的面积S_{1}$。

答案:
16.解:
(1)
∵∠AOB=60°,半径R=3,
∴$S_{扇形AOB}=\frac{60π×3²}{360}=\frac{3π}{2}$.
∵OA=OB,∠AOB=60°,
∴△OAB是等边三角形,
∴$S_{△OAB}=\frac{1}{2}×3×\sqrt{3² - (\frac{3}{2})²}=\frac{9\sqrt{3}}{4}$,
∴阴影部分的面积$S_{阴}=\frac{3π}{2}-\frac{9\sqrt{3}}{4}$.
(2)如图,设$\odot O_{1}$与OA相切于点E,连接$O_{1}O,O_{1}E$,
∵相切两圆的连心线必过切点,
∴O,$O_{1}$,C三点共线,
∴$∠EOO_{1}=\frac{1}{2}∠AOB=30°,∠OEO_{1}=90°$.在Rt△$OO_{1}E$中,
∵$∠EOO_{1}=30°$,
∴$OO_{1}=2O_{1}E$,
∴$\odot O_{1}$的半径$O_{1}E=1$,
∴$S_{1}=πr²=π$.
16.解:
(1)
∵∠AOB=60°,半径R=3,
∴$S_{扇形AOB}=\frac{60π×3²}{360}=\frac{3π}{2}$.
∵OA=OB,∠AOB=60°,
∴△OAB是等边三角形,
∴$S_{△OAB}=\frac{1}{2}×3×\sqrt{3² - (\frac{3}{2})²}=\frac{9\sqrt{3}}{4}$,
∴阴影部分的面积$S_{阴}=\frac{3π}{2}-\frac{9\sqrt{3}}{4}$.
(2)如图,设$\odot O_{1}$与OA相切于点E,连接$O_{1}O,O_{1}E$,
∵相切两圆的连心线必过切点,
∴O,$O_{1}$,C三点共线,
∴$∠EOO_{1}=\frac{1}{2}∠AOB=30°,∠OEO_{1}=90°$.在Rt△$OO_{1}E$中,
∵$∠EOO_{1}=30°$,
∴$OO_{1}=2O_{1}E$,
∴$\odot O_{1}$的半径$O_{1}E=1$,
∴$S_{1}=πr²=π$.

查看更多完整答案,请扫码查看


