《2025年全科王同步课时练习九年级数学上册人教版》

10. (数学文化)我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,此公式与古希腊几何学家海伦提出的公式如出一辙,即三角形的三边长分别为$a,b,c$,记$p= \frac{a + b + c}{2}$,则其面积$S= \sqrt{p(p - a)(p - b)(p - c)}$,这个公式也被称为海伦—秦九韶公式。若$p = 5$,$c = 2$,则此三角形面积的最大值为($\sqrt{15}$)
A.$\sqrt{3}$
B.$\frac{\sqrt{15}}{2}$
C.$\sqrt{15}$
D.$5$

答案： C[提示:
∵p=$\frac{a + b + c}{2}$,p=5,c=2,
∴5=$\frac{a + b + 2}{2}$,
∴a + b=8,
∴a=8 -b,
∴S=$\sqrt{p(p - a)(p - b)(p - c)}$=$\sqrt{5(5 - a)(5 - b)(5 - 2)}$=$\sqrt{15(5 - a)(5 - b)}$=$\sqrt{15b(8 - b)-225}$=$\sqrt{-15b^2 + 120b - 225}$=$\sqrt{-15(b - 4)^2 + 15}$.当b=4时,S有最大值,为$\sqrt{15}$.]

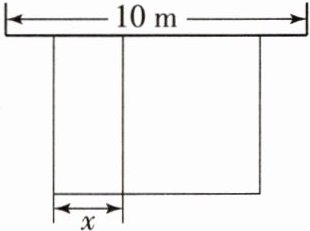
11. 某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为$10m$),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为$1:2$的矩形,已知栅栏的总长度为$24m$,设较小矩形的宽为$x m$(如图)。
(1)若矩形养殖场的总面积为$36m^{2}$,求此时$x$的值；
(2)当$x$为多少时,矩形养殖场的总面积最大？最大值为多少？

答案： 解:
(1)根据题意知较大矩形的宽为2x m,长为$\frac{24 - x - 2x}{3}$=(8 -x)m,
∴(x + 2x)(8 -x)=36,解得x=2或x=6.当x=6时,3x=18＞10,不符合题意,舍去,
∴x=2.答:此时x的值为2.
(2)设矩形养殖场的总面积是y m²,
∵墙的长度为10 m,
∴0＜x≤$\frac{10}{3}$.根据题意得y=(x + 2x)(8 -x)=$-3x^2 + 24x=-3(x - 4)^2 + 48$.
∵-3＜0,
∴当x=$\frac{10}{3}$时,y取最大值,最大值为$-3×(\frac{10}{3}-4)^2 + 48=\frac{140}{3}$(m²).答:当x=$\frac{10}{3}$时,矩形养殖场的总面积最大,最大值为$\frac{140}{3}$m².

12. (综合实践题)问题情境
小莹妈妈的花卉超市以$15$元/盆的价格新购进了某种盆栽花卉,为了确定售价,小莹帮妈妈调查了附近$A,B,C,D,E$五家花卉店近期该种盆栽花卉的售价与日销售量情况,记录如下表：

数据整理
(1)请将以上调查数据按照一定顺序重新整理,填写在下表中：

模型建立
(2)分析数据的变化规律,找出日销售量与售价间的关系。
拓广应用
(3)根据以上信息,小莹妈妈在销售该种花卉中,
①要想每天获得$400$元的利润,应如何定价？
②售价定为多少时,每天能够获得最大利润？
(1)根据销售单价从小到大排列得下表: 售价(元/盆) 18 20 22 26 30 日销售量(盆) 54 50 46 38 30
(2)观察表格知销售量是售价的一次函数.设销售量为y盆,售价为x元,y=kx + b,把(18,54),(20,50)代入,得$\begin{cases}18k + b = 54, \\20k + b = 50,\end{cases}$解得$\begin{cases}k=-2, \\b=90,\end{cases}$
∴y=-2x + 90.
(3)①
∵每天获得400元的利润,
∴(x - 15)(-2x + 90)=400,解得x=25或x=35,
∴要想每天获得400元的利润,定价为25元或35元. ②设每天获得的利润为w元,根据题意,得w=(x - 15)(-2x + 90)=$-2x^2 + 120x - 1350=-2(x - 30)^2 + 450$,
∵-2＜0,
∴当x=30时,w取最大值450,
∴售价定为30元时,每天能够获得最大利润450元.

答案： 解:
(1)根据销售单价从小到大排列得下表: 售价(元/盆) 18 20 22 26 30 日销售量(盆) 54 50 46 38 30
(2)观察表格知销售量是售价的一次函数.设销售量为y盆,售价为x元,y=kx + b,把(18,54),(20,50)代入,得$\begin{cases}18k + b = 54, \\20k + b = 50,\end{cases}$解得$\begin{cases}k=-2, \\b=90,\end{cases}$
∴y=-2x + 90.
(3)①
∵每天获得400元的利润,
∴(x - 15)(-2x + 90)=400,解得x=25或x=35,
∴要想每天获得400元的利润,定价为25元或35元. ②设每天获得的利润为w元,根据题意,得w=(x - 15)(-2x + 90)=$-2x^2 + 120x - 1350=-2(x - 30)^2 + 450$,
∵-2＜0,
∴当x=30时,w取最大值450,
∴售价定为30元时,每天能够获得最大利润450元.

13. (素养题)[2023·四川南充中考]某工厂计划从$A,B$两种产品中选择一种生产并销售,每日产销$x$件。已知$A产品成本价m$(元/件)($m$为常数,且$4\leq m\leq6$),售价$8$元/件,每日最多产销$500$件,同时每日共支付专利费$30$元；$B产品成本价12$元/件,售价$20$元/件,每日最多产销$300$件,同时每日支付专利费$y$元,$y$(元)与每日产销$x$(件)满足关系式$y = 80 + 0.01x^{2}$。
(1)若产销$A,B两种产品的日利润分别为w_{1}$元,$w_{2}$元,请分别写出$w_{1},w_{2}与x$的函数关系式,并写出$x$的取值范围。
(2)分别求出产销$A,B$两种产品的最大日利润。($A产品的最大日利润用含m$的代数式表示)
(3)为获得最大日利润,该工厂应该选择产销哪种产品？并说明理由。
【利润$=$(售价$-$成本)$×产销数量-$专利费】

答案： 解:
(1)根据题意,得$w_1=(8 - m)x - 30(0\leq x\leq500)$.$w_2=(20 - 12)x-(80 + 0.01x^2)=-0.01x^2 + 8x - 80(0\leq x\leq300)$.
(2)
∵8 - m＞0,
∴$w_1$随x的增大而增大,又0≤x≤500,
∴当x=500时,$w_{1最大}=-500m + 3970$.
∵$w_2=-0.01x^2 + 8x - 80=-0.01(x - 400)^2 + 1520$,又-0.01＜0,对称轴x=400,
∴当0≤x≤300时,$w_2$随x的增大而增大,
∴当x=300时,$w_{2最大}=-0.01×(300 - 400)^2 + 1520=1420$(元).
(3)①若$w_{1最大}=w_{2最大}$,即-500m + 3970=1420,解得m=5.1. ②若$w_{1最大}＞w_{2最大}$,即-500m + 3970＞1420,解得m＜5.1. ③若$w_{1最大}＜w_{2最大}$,即-500m + 3970＜1420,解得m＞5.1.又4≤m≤6,综上可得,为获得最大日利润,当m=5.1时,选择A,B产品产销均可;当4≤m＜5.1时,选择A种产品产销;当5.1＜m≤6时,选择B种产品产销.答:当A产品成本价为5.1元时,工厂选择A或B产品产销日利润一样大,当4≤m＜5.1时,工厂选择A产品产销日利润最大,当5.1＜m≤6时,工厂选择B产品产销日利润最大.