《2025年全科王同步课时练习九年级数学上册人教版》

1. (跨学科融合题)自由落体公式 $ h = \frac{1}{2}gt^{2} $($ g $ 为常量),$ h $ 与 $ t $ 之间的关系是 (C)
A.正比例函数
B.一次函数
C.二次函数
D.以上答案都不对

答案： C

2. 下列函数中,属于二次函数的是 (D)
A.$ y = x + 4 $
B.$ y = (x - 3)^{2} - x^{2} $
C.$ y = \frac{1}{x^{2}} - x $
D.$ y = 2(x + 1)^{2} + 5 $

答案： D

3. 函数 $ y = x^{m + 1} $ 是关于 $ x $ 的二次函数,则 $ m $ 的值为 (C)
A.$ -1 $
B.$ 0 $
C.$ 1 $
D.$ 2 $

答案： C[提示:根据二次函数的定义得$m+1=2$,解得$m=1$.]

4. 若关于 $ x $ 的函数 $ y = (2 - a)x^{2} - x $ 是二次函数,则 $ a $ 的取值范围是 (B)
A.$ a \neq 0 $
B.$ a \neq 2 $
C.$ a ＜ 2 $
D.$ a ＞ 2 $

答案： B[提示:
∵ 关于x的函数$y=(2-a)x^{2}-x$是二次函数,
∴ 2$-a≠0$,即$a≠2$.]

5. 下列具有二次函数关系的是 (C)
A.正方形的周长 $ y $ 与边长 $ x $
B.速度一定时,路程 $ s $ 与时间 $ t $
C.正方形的面积 $ y $ 与边长 $ x $
D.三角形的高一定时,面积 $ y $ 与底边长 $ x $

答案： C

6. (易错题)若函数 $ y = (m - 2)x^{|m|} + 1 $($ m $ 是常数)是二次函数,则 $ m $ 的值是-2。

答案： -2

7. 下列二次函数中,二次项系数是 $ -3 $ 的是 (C)
A.$ y = 3x^{2} - 2x + 5 $
B.$ y = x^{2} - 3x + 2 $
C.$ y = -3x^{2} - x $
D.$ y = x^{2} - 3 $

答案： C

8. 关于函数 $ y = (500 - 10x)(40 + x) $,下列说法不正确的是 (C)
A.$ y $ 是 $ x $ 的二次函数
B.二次项系数是 $ -10 $
C.一次项是 $ 100 $
D.常数项是 $ 20000 $

答案： C[提示:整理,得$y=-10x^{2}+100x+20000$,故y是x的二次函数,二次项系数是-10,一次项是100x,常数项是20000.]

9. (教材改编题)某种药品售价为每盒 $ 300 $ 元,经过医保局连续两次“灵魂砍价”,药品企业同意降价若干进入国家医保用药目录。如果每次降价的百分率都是 $ x $,那么两次降价后的价格 $ y $(元)与每次降价的百分率 $ x $ 之间的函数关系式是 (B)
A.$ y = 300(1 - x) $
B.$ y = 300(1 - x)^{2} $
C.$ y = 300(1 + x) $
D.$ y = 300(1 + x)^{2} $

答案： B

10. 已知一个直角三角形两直角边长的和为 $ 10 $,设其中一条直角边长为 $ x $,则直角三角形的面积 $ y $ 与 $ x $ 之间的函数关系式是 (A)
A.$ y = -\frac{1}{2}x^{2} + 5x $
B.$ y = -x^{2} + 10x $
C.$ y = \frac{1}{2}x^{2} + 5x $
D.$ y = x^{2} + 10x $

答案： A[提示:若其中一条直角边长为x,则另一条直角边长为$(10-x)$,依题意,得$y=\frac {1}{2}x(10-x)=-\frac {1}{2}x^{2}+5x$.]

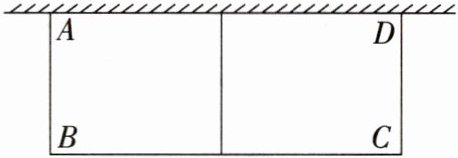
11. 如图,在一面靠墙的空地上用长为 $ 24 $ 米的篱笆,围成中间隔有一道篱笆的长方形花圃,设花圃的宽 $ AB $ 为 $ x $ 米,面积为 $ S $ 平方米。
(1) 求 $ S $ 与 $ x $ 的函数关系式及自变量 $ x $ 的取值范围；
(2) 若墙的最大可用长度为 $ 9 $ 米,求此时自变量 $ x $ 的取值范围。

答案： 解:
(1)$S=BC\cdot AB=(24-3x)x=-3x^{2}+24x$,由题意,得$\left\{\begin{array}{l} 24-3x＞0,\\ x＞0,\end{array}\right. $解得$0＜x＜8$.
(2)$\because 24-3x≤9,\therefore x≥5$.结合
(1)得$5≤x＜8.$