第28页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
11. (易错题) 对于二次函数 $ y = 2x^2 - 3 $,当 $ -1 \leq x \leq 2 $ 时,$ y $ 的取值范围是 (
A.$ -1 \leq y \leq 5 $
B.$ -5 \leq y \leq 5 $
C.$ -3 \leq y \leq 5 $
D.$ -2 \leq y \leq 5 $
C
)A.$ -1 \leq y \leq 5 $
B.$ -5 \leq y \leq 5 $
C.$ -3 \leq y \leq 5 $
D.$ -2 \leq y \leq 5 $
答案:
C[提示:
∵ 二次函数的解析式为y = 2x² - 3,
∴ 抛物线的对称轴为直线x = 0.
∵ a = 2 > 0,
∴ 抛物线开口向上.
∵ -1 ≤ x ≤ 2,当x = 0时,取得最小值y = -3,当x = -1时,y = -1,当x = 2时,y = 5,
∴ 当 -1 ≤ x ≤ 2时,y的取值范围是 -3 ≤ y ≤ 5.]
[易错警示] 当自变量取值范围在对称轴的同侧时,直接利用增减性确定函数值的取值范围,当自变量的取值范围分布在对称轴的两侧时,确定函数值取值范围要考虑顶点坐标.
∵ 二次函数的解析式为y = 2x² - 3,
∴ 抛物线的对称轴为直线x = 0.
∵ a = 2 > 0,
∴ 抛物线开口向上.
∵ -1 ≤ x ≤ 2,当x = 0时,取得最小值y = -3,当x = -1时,y = -1,当x = 2时,y = 5,
∴ 当 -1 ≤ x ≤ 2时,y的取值范围是 -3 ≤ y ≤ 5.]
[易错警示] 当自变量取值范围在对称轴的同侧时,直接利用增减性确定函数值的取值范围,当自变量的取值范围分布在对称轴的两侧时,确定函数值取值范围要考虑顶点坐标.
12. 下列图象中,函数 $ y = ax^2 - a(a \neq 0) $ 与 $ y = ax + a $ 的图象大致是 (
]

C
)]

答案:
C[提示:当a > 0时,由二次函数y = ax² - a知图象开口向上,顶点在y轴负半轴上,与x轴的交点为(-1,0),(1,0),由一次函数y = ax + a知图象过第一、二、三象限,交x轴于(-1,0).当a < 0时,由二次函数y = ax² - a知图象开口向下,顶点在y轴正半轴上,与x轴的交点为(-1,0),(1,0),由一次函数y = ax + a知图象过第二、三、四象限,交x轴于(-1,0).]
13. 抛物线 $ y = x^2 + 3 $ 上有两点 $ A(x_1, y_1) $,$ B(x_2, y_2) $,若 $ y_1 < y_2 $,则下列结论正确的是 (
A.$ 0 \leq x_1 < x_2 $
B.$ x_2 < x_1 \leq 0 $
C.$ x_2 < x_1 \leq 0 $ 或 $ 0 \leq x_1 < x_2 $
D.以上都不对
D
)A.$ 0 \leq x_1 < x_2 $
B.$ x_2 < x_1 \leq 0 $
C.$ x_2 < x_1 \leq 0 $ 或 $ 0 \leq x_1 < x_2 $
D.以上都不对
答案:
D[提示:抛物线y = x² + 3开口向上,对称轴为y轴,
∵ 抛物线y = x² + 3上有两点A(x₁,y₁),B(x₂,y₂),且y₁ < y₂,
∴ |x₁| < |x₂|,
∴ 0 ≤ x₁ < x₂或x₂ < x₁ ≤ 0或0 < -x₁ < x₂或0 < x₁ < -x₂.]
[解题技巧] 已知函数值的大小关系确定自变量的大小关系时,一般要分在对称轴左侧和右侧两种情况讨论.
∵ 抛物线y = x² + 3上有两点A(x₁,y₁),B(x₂,y₂),且y₁ < y₂,
∴ |x₁| < |x₂|,
∴ 0 ≤ x₁ < x₂或x₂ < x₁ ≤ 0或0 < -x₁ < x₂或0 < x₁ < -x₂.]
[解题技巧] 已知函数值的大小关系确定自变量的大小关系时,一般要分在对称轴左侧和右侧两种情况讨论.
14. 两条抛物线 $ y_1 = -\frac{1}{2}x^2 + 1 $,$ y_2 = -\frac{1}{2}x^2 - 1 $ 分别经过点 $ (-2, -1) $,$ (2, -3) $,则它们与平行于 $ y $ 轴的两条平行线 $ x = 2 $,$ x = -2 $ 围成的面积 (如图阴影部分) 为 (
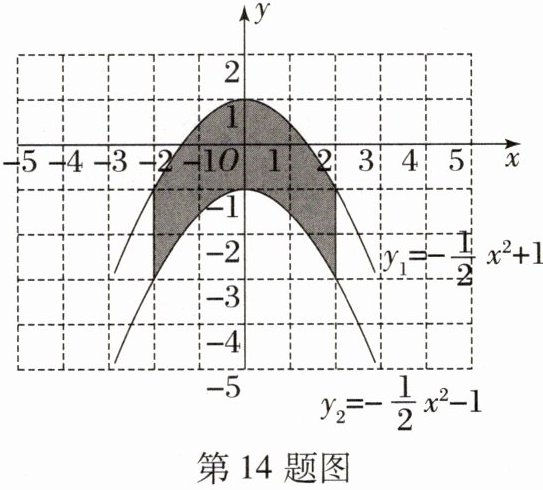
A.8
B.6
C.10
D.4
A
)
A.8
B.6
C.10
D.4
答案:
A[提示:
∵ 两解析式的二次项系数相同,
∴ 两抛物线的形状相同,
∴ y₁ - y₂ = -$\frac{1}{2}$x² + 1 - (-$\frac{1}{2}$x² - 1) = 2,
∴ S阴影 = (y₁ - y₂)×|2 - (-2)| = 2×4 = 8.]
∵ 两解析式的二次项系数相同,
∴ 两抛物线的形状相同,
∴ y₁ - y₂ = -$\frac{1}{2}$x² + 1 - (-$\frac{1}{2}$x² - 1) = 2,
∴ S阴影 = (y₁ - y₂)×|2 - (-2)| = 2×4 = 8.]
15. (2023·广东中考) 如图,抛物线 $ y = ax^2 + c $ 经过正方形 $ OABC $ 的三个顶点 $ A $,$ B $,$ C $,点 $ B $ 在 $ y $ 轴上,则 $ ac $ 的值为 ( )
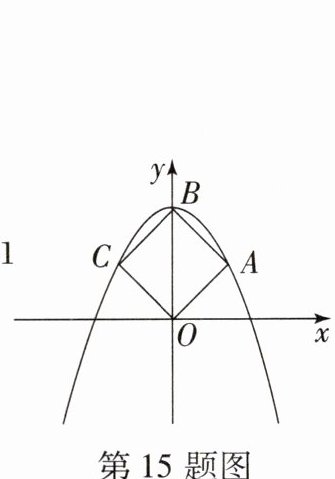
A.-1
B.-2
C.-3
D.-4

A.-1
B.-2
C.-3
D.-4
答案:
B[提示:如图,过A作AH⊥x轴于H,
∵ 四边形ABCO是正方形,
∴ ∠AOB = 45°,
∴ ∠AOH = 45°,
∴ AH = OH.设A(m,m),则B(0,2m),
∴ $\begin{cases}m = am² + c\\2m = c\end{cases}$,解得am = -1,m = $\frac{c}{2}$,
∴ ac = -2.]

B[提示:如图,过A作AH⊥x轴于H,
∵ 四边形ABCO是正方形,
∴ ∠AOB = 45°,
∴ ∠AOH = 45°,
∴ AH = OH.设A(m,m),则B(0,2m),
∴ $\begin{cases}m = am² + c\\2m = c\end{cases}$,解得am = -1,m = $\frac{c}{2}$,
∴ ac = -2.]

16. 如图,在平面直角坐标系中,抛物线 $ y = ax^2 + 3 $ 与 $ y $ 轴交于点 $ A $,过点 $ A $ 作与 $ x $ 轴平行的直线交抛物线 $ y = \frac{1}{3}x^2 $ 于点 $ B $,$ C $,则 $ BC $ 的长为
]

6
。]

答案:
6[提示:
∵ 抛物线y = ax² + 3与y轴交于点A,
∴ 点A坐标为(0,3).当y = 3时,$\frac{1}{3}$x² = 3,解得x = ±3,
∴ 点B坐标为(-3,3),点C坐标为(3,3),
∴ BC = 3 - (-3) = 6.]
∵ 抛物线y = ax² + 3与y轴交于点A,
∴ 点A坐标为(0,3).当y = 3时,$\frac{1}{3}$x² = 3,解得x = ±3,
∴ 点B坐标为(-3,3),点C坐标为(3,3),
∴ BC = 3 - (-3) = 6.]
17. 如图,抛物线 $ y_1 = -\frac{3}{4}x^2 + 3 $ 与 $ x $ 轴交于 $ A $,$ B $ 两点,直线 $ y_2 = -\frac{3}{4}x + b $ 与 $ y_1 $ 交于 $ B $,$ C $ 两点。
(1) 求直线 $ BC $ 对应的函数解析式和点 $ C $ 的坐标;
(2) 点 $ P $ 为抛物线上异于点 $ C $ 的一点,若 $ S_{\triangle PAB} = S_{\triangle ABC} $,求点 $ P $ 的坐标。
]
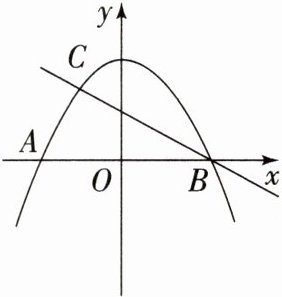
(1) 求直线 $ BC $ 对应的函数解析式和点 $ C $ 的坐标;
(2) 点 $ P $ 为抛物线上异于点 $ C $ 的一点,若 $ S_{\triangle PAB} = S_{\triangle ABC} $,求点 $ P $ 的坐标。
]

答案:
解:
(1)由 -$\frac{3}{4}$x² + 3 = 0得x = 2或x = -2,
∴ 点B坐标为(2,0).把(2,0)代入y = -$\frac{3}{4}$x + b,得b = $\frac{3}{2}$,
∴ BC所在直线解析式为y = -$\frac{3}{4}$x + $\frac{3}{2}$.由 -$\frac{3}{4}$x² + 3 = -$\frac{3}{4}$x + $\frac{3}{2}$得x = 2或x = -1,当x = -1时,y = -$\frac{3}{4}$×(-1) + $\frac{3}{2}$ = $\frac{9}{4}$,
∴ 点C坐标为(-1,$\frac{9}{4}$).
(2)由y = -$\frac{3}{4}$x² + 3得抛物线对称轴为y轴,
∴ 点C关于y轴对称的点P坐标为(1,$\frac{9}{4}$).把y = $\frac{9}{4}$代入y = -$\frac{3}{4}$x² + 3得$\frac{9}{4}$ = -$\frac{3}{4}$x² + 3,解得x = 1或x = -1.
∴ 点P坐标为(1,$\frac{9}{4}$).把y = -$\frac{9}{4}$代入y = -$\frac{3}{4}$x² + 3,得 -$\frac{9}{4}$ = -$\frac{3}{4}$x² + 3,解得x = √7或x = -√7,
∴ 点P坐标为(√7,-$\frac{9}{4}$)或(-√7,-$\frac{9}{4}$).综上,点P坐标为(1,$\frac{9}{4}$)或(√7,-$\frac{9}{4}$)或(-√7,-$\frac{9}{4}$).
(1)由 -$\frac{3}{4}$x² + 3 = 0得x = 2或x = -2,
∴ 点B坐标为(2,0).把(2,0)代入y = -$\frac{3}{4}$x + b,得b = $\frac{3}{2}$,
∴ BC所在直线解析式为y = -$\frac{3}{4}$x + $\frac{3}{2}$.由 -$\frac{3}{4}$x² + 3 = -$\frac{3}{4}$x + $\frac{3}{2}$得x = 2或x = -1,当x = -1时,y = -$\frac{3}{4}$×(-1) + $\frac{3}{2}$ = $\frac{9}{4}$,
∴ 点C坐标为(-1,$\frac{9}{4}$).
(2)由y = -$\frac{3}{4}$x² + 3得抛物线对称轴为y轴,
∴ 点C关于y轴对称的点P坐标为(1,$\frac{9}{4}$).把y = $\frac{9}{4}$代入y = -$\frac{3}{4}$x² + 3得$\frac{9}{4}$ = -$\frac{3}{4}$x² + 3,解得x = 1或x = -1.
∴ 点P坐标为(1,$\frac{9}{4}$).把y = -$\frac{9}{4}$代入y = -$\frac{3}{4}$x² + 3,得 -$\frac{9}{4}$ = -$\frac{3}{4}$x² + 3,解得x = √7或x = -√7,
∴ 点P坐标为(√7,-$\frac{9}{4}$)或(-√7,-$\frac{9}{4}$).综上,点P坐标为(1,$\frac{9}{4}$)或(√7,-$\frac{9}{4}$)或(-√7,-$\frac{9}{4}$).
18. (素养题) 已知抛物线 $ y = \frac{1}{4}x^2 + 1 $ 具有如下性质:给抛物线上任意一点到定点 $ F(0, 2) $ 的距离与到 $ x $ 轴的距离相等,如图,点 $ M $ 的坐标为 $ (\sqrt{3}, 3) $,$ P $ 是抛物线 $ y = \frac{1}{4}x^2 + 1 $ 上一动点。
(1) 当 $ \triangle POF $ 面积为 4 时,求 $ P $ 点的坐标;
(2) 求 $ \triangle PMF $ 周长的最小值。
]
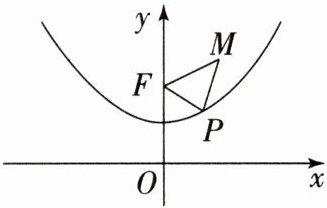
(1) 当 $ \triangle POF $ 面积为 4 时,求 $ P $ 点的坐标;
(2) 求 $ \triangle PMF $ 周长的最小值。
]

答案:
解:
(1)设P点的坐标为(x,$\frac{1}{4}$x² + 1),
∵ 点F的坐标为(0,2),
∴ OF = 2,
∴ 当S△POF = 4时,$\frac{1}{2}$×2×|x| = 4,解得x = ±4,
∴ y = $\frac{1}{4}$×(±4)² + 1 = 5,
∴ 点P的坐标为(-4,5)或(4,5).
(2)如图,过点M作ME⊥x轴于点E,交抛物线y = $\frac{1}{4}$x² + 1于点P',
∵ 抛物线上任意一点到点F(0,2)的距离与到x轴的距离相等,
∴ P'F = P'E,又MF为定值,
∴ 当点P运动到点P'时,△PMF周长取最小值.
∵ F(0,2),M(√3,3),
∴ ME = 3,FM = $\sqrt{(√3 - 0)² + (3 - 2)²}$ = 2,
∴ △PMF周长的最小值为ME + FM = 3 + 2 = 5.

解:
(1)设P点的坐标为(x,$\frac{1}{4}$x² + 1),
∵ 点F的坐标为(0,2),
∴ OF = 2,
∴ 当S△POF = 4时,$\frac{1}{2}$×2×|x| = 4,解得x = ±4,
∴ y = $\frac{1}{4}$×(±4)² + 1 = 5,
∴ 点P的坐标为(-4,5)或(4,5).
(2)如图,过点M作ME⊥x轴于点E,交抛物线y = $\frac{1}{4}$x² + 1于点P',
∵ 抛物线上任意一点到点F(0,2)的距离与到x轴的距离相等,
∴ P'F = P'E,又MF为定值,
∴ 当点P运动到点P'时,△PMF周长取最小值.
∵ F(0,2),M(√3,3),
∴ ME = 3,FM = $\sqrt{(√3 - 0)² + (3 - 2)²}$ = 2,
∴ △PMF周长的最小值为ME + FM = 3 + 2 = 5.

查看更多完整答案,请扫码查看


