《2025年全科王同步课时练习九年级数学上册人教版》

1. 下列抛物线中,开口向下并且开口最大的是(B)
A.$ y = x^{2} $
B.$ y = -\frac{2}{3}x^{2} $
C.$ y = \frac{1}{5}x^{2} $
D.$ y = -\sqrt{3}x^{2} $

答案： B[提示:
∵抛物线开口向下,
∴二次项系数小于0.
∵|-2/3|＜|$-\sqrt{3}$|,
∴抛物线$y=-\frac{2}{3}x^{2}$的开口最大.]

2. (2023·安徽中考)下列函数中,$ y 的值随 x $值的增大而减小的是(D)
A.$ y = x^{2} + 1 $
B.$ y = -x^{2} + 1 $
C.$ y = 2x + 1 $
D.$ y = -2x + 1 $

答案： D[提示:A中,函数$y=x^{2}+1,$当x＜0时,y随x的增大而减小,当x＞0时,y随x的增大而增大;B中,函数$y=-x^{2}+1,$当x＞0时,y随x的增大而减小,当x＜0时,y随x的值增大而增大;C中,函数y=2x+1,y随x的增大而增大;D中,函数y=-2x+1,y随x的增大而减小.]

3. 抛物线的解析式为$ y = 3(x - 2)^{2} + 1 $,若将$ x $轴向上平移2个单位长度,将$ y $轴向左平移3个单位长度,则该抛物线在新的平面直角坐标系中的解析式为(C)
A.$ y = 3(x + 1)^{2} + 3 $
B.$ y = 3(x - 5)^{2} + 3 $
C.$ y = 3(x - 5)^{2} - 1 $
D.$ y = 3(x + 1)^{2} - 1 $

答案： C[提示:根据题意知,将抛物线$y=3(x-2)^{2}+1$向下平移2个单位长度,再向右平移3个单位长度后,所得抛物线解析式为$y=3(x-5)^{2}-1.]$

4. (2023·湖南株洲中考)如图,直线$ l 为二次函数 y = ax^{2} + bx + c(a \neq 0) $的图象的对称轴,则下列说法正确的是(C)

A.$ b $恒大于0
B.$ a $,$ b $同号
C.$ a $,$ b $异号
D.以上说法都不对

答案： C[提示:
∵直线l为二次函数$y=ax^{2}+bx+c(a≠0)$的图象的对称轴,
∴对称轴为直线$x=-\frac{b}{2a}＞0.$当a＜0时,则b＞0;当a＞0时,则b＜0.
∴a,b异号.]

5. 已知抛物线$ y = x^{2} + mx 的对称轴为直线 x = 2 $,则关于$ x 的方程 x^{2} + mx = 5 $的根是(D)
A.0,4
B.1,5
C.1,-5
D.-1,5

答案： D[提示:
∵抛物线$y=x^{2}+mx$的对称轴为直线x=2,
∴$-\frac{m}{2}=2,$解得m=-4,
∴方程$x^{2}+mx=5$可以写成$x^{2}-4x=5,$
∴$x^{2}-4x-5=0,$
∴(x-5)(x+1)=0,解得$x_{1}=5,x_{2}=-1.]$

6. 已知函数$ y = 2(x - 1)^{2} $,当$ -1 \leq x \leq 2 $时,$ y $的最大值与最小值的和为(8)
A.8
B.10
C.2
D.0

答案： A[提示:
∵函数$y=2(x-1)^{2}$中,a=2＞0,
∴函数图象开口向上,顶点坐标为(1,0),
∴$y_{最小}=0.$
∵-1≤x≤2,
∴当x=-1时$,y_{最大}=2×(-1-1)^{2}=2×4=8.$
∴y的最大值与最小值的和为8+0=8.]

7. 如图,点$ A $,$ B 的坐标分别为 (2,5) 和 (5,5) $,抛物线$ y = a(x - m)^{2} + n 的顶点在线段 AB $上运动(抛物线随顶点一起平移),与$ x 轴交于 C $,$ D $两点($ C 在 D $的左侧),点$ C $横坐标的最小值为-3,则点$ D $横坐标的最大值为(10)

A.2
B.10
C.5
D.9

答案： B[提示:当点C横坐标为-3时,抛物线顶点为A(2,5),对称轴为x=2,此时D点横坐标为7,则CD=10.当抛物线顶点为B(5,5)时,抛物线对称轴为x=5,且CD=10,故C(0,0),D(10,0).由于此时D点横坐标最大,故点D横坐标的最大值为10.]

8. 已知二次函数$ y = x^{2} + ax + b $($ a $,$ b $为常数).命题①：该函数的图象经过点$ (1,0) $；命题②：该函数的图象经过点$ (3,0) $；命题③：该函数的图象与$ x 轴的交点位于 y $轴的两侧；命题④：该函数的图象的对称轴为直线$ x = 1 $.如果这四个命题中只有一个命题是假命题,则这个假命题是(A)
A.命题①
B.命题②
C.命题③
D.命题④

答案： A[提示:假设抛物线的对称轴为直线x=1,则$-\frac{a}{2}=1,$解得a=-2.
∵函数的图象经过点(3,0),
∴3a+b+9=0,解得b=-3,故抛物线的解析式为$y=x^{2}-2x-3.$当y=0时,得$x^{2}-2x-3=0,$解得x=3或x=-1,故抛物线与x轴的交点为(-1,0)和(3,0),函数的图象与x轴的交点位于y轴的两侧.故命题②③④都正确,①错误.]

9. 二次函数$ y = ax^{2} + bx + 1 与一次函数 y = 2ax + b $在同一平面直角坐标系中的图象可能是(A)

A.
B.
C.
D.

答案： A[提示:A中,由抛物线可知a＞0,b＜0,c=1,对称轴为直线$x=-\frac{b}{2a},$由直线可知a＞0,b＜0,直线经过点$(-\frac{b}{2a},0);B$中,由抛物线可知对称轴为直线$x=-\frac{b}{2a},$直线不经过点$(-\frac{b}{2a},0);C$中,由抛物线可知对称轴为直线$x=-\frac{b}{2a},$直线不经过点$(-\frac{b}{2a},0);D$中,由抛物线可知对称轴为直线$x=-\frac{b}{2a},$直线不经过点$(-\frac{b}{2a},0).]$

10. 已知二次函数$ y = -ax^{2} + 2ax + 3(a ＞ 0) $,若点$ P(m,3) $在该函数的图象上,且$ m \neq 0 $,则$ m $的值为2.

答案： 2[提示:
∵点P(m,3)在二次函数$y=-ax^{2}+2ax+3(a＞0)$的图象上,
∴$3=-am^{2}+2am+3,$
∴-am(m-2)=0,解得m=2或m=0(舍去).]

11. 若二次函数$ y = x^{2} - 2x - 3 的图象上有且只有三个点到 x 轴的距离等于 m $,则$ m $的值为4.

答案： 4[提示:
∵$y=x^{2}-2x-3=(x-1)^{2}-4,$
∴抛物线开口向上,抛物线对称轴为直线x=1,顶点为(1,-4),
∴顶点到x轴的距离为4.
∵函数图象上有三个点到x轴的距离为m,
∴m=4.]

12. (2023·湖北襄阳中考)如图,一位篮球运动员投篮时,球从$ A $点出手后沿抛物线行进,篮球出手后距离地面的高度$ y(m) $与篮球距离出手点的水平距离$ x(m) $之间的函数关系是 $ y = -\frac{1}{5}(x - \frac{3}{2})^{2} + \frac{7}{2} $.下列说法正确的是______(填序号).

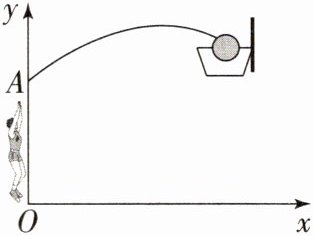
①篮球行进过程中距离地面的最大高度为3.5m；
②篮球出手点距离地面的高度为2.25m.
①

答案： ①[提示:由$y=-\frac{1}{5}(x-\frac{3}{2})^{2}+\frac{7}{2}$的顶点为(1.5,3.5),得篮球行进过程中距离地面的最大高度为3.5m,即①正确.当x=0时,y=-0.2×2.25+3.5=3.05,即②不正确.]

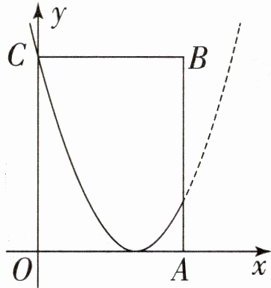
13. (2023·浙江绍兴中考)在平面直角坐标系$ xOy $中,一个图形上的点都在一边平行于$ x $轴的矩形内部(包括边界),这些矩形中面积最小的矩形称为该图形的关联矩形.例如：如图,函数$ y = (x - 2)^{2}(0 \leq x \leq 3) $的图象(抛物线中的实线部分),它的关联矩形为矩形$ OABC $.若二次函数$ y = \frac{1}{4}x^{2} + bx + c(0 \leq x \leq 3) 图象的关联矩形恰好也是矩形 OABC $,则$ b = $$\frac{7}{12}$或$-\frac{25}{12}$.

答案： $\frac{7}{12}$或$-\frac{25}{12}[$提示:由$y=(x-2)^{2}(0≤x≤3),$当x=0时,y=4,
∴C(0,4).
∵A(3,0),四边形ABCO是矩形,
∴B(3,4).①当抛物线经过O,B时,将点O(0,0),B(3,4)代入$y=\frac{1}{4}x^{2}+bx+c(0≤x≤3),$得$\begin{cases} c=0, \\ \frac{1}{4}×9+3b+c=4 \end{cases}$解得$b=\frac{7}{12}.②$当抛物线经过A,C时,将点A(3,0),C(0,4)代入$y=\frac{1}{4}x^{2}+bx+c(0≤x≤3),$得$\begin{cases} c=4, \\ \frac{1}{4}×9+3b+c=0 \end{cases}$解得$b=-\frac{25}{12}.$综上$,b=\frac{7}{12}$或$b=-\frac{25}{12}.]$