第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. (湖南株洲中考)已知二次函数 $ y = ax^{2} + bx - c $ ($ a \neq 0 $),其中 $ b > 0 $,$ c > 0 $,则该函数的图象可能为 (

C
)
答案:
C[提示:
∵c>0,
∴−c<0,故A,D选项不符合题意.当a>0时,
∵b>0,
∴对称轴x=−$\frac{b}{2a}$<0,故B选项不符合题意.当a<0时,b>0,
∴对称轴x=−$\frac{b}{2a}$>0,故C选项符合题意.]
∵c>0,
∴−c<0,故A,D选项不符合题意.当a>0时,
∵b>0,
∴对称轴x=−$\frac{b}{2a}$<0,故B选项不符合题意.当a<0时,b>0,
∴对称轴x=−$\frac{b}{2a}$>0,故C选项符合题意.]
2. (2023·陕西中考A卷)在平面直角坐标系中,二次函数 $ y = x^{2} + mx + m^{2} - m $ ( $ m $ 为常数)的图象经过点 $ (0,6) $,其对称轴在 $ y $ 轴左侧,则该二次函数有 (
A.最大值 $ 5 $
B.最大值 $ \frac{15}{4} $
C.最小值 $ 5 $
D.最小值 $ \frac{15}{4} $
D
)A.最大值 $ 5 $
B.最大值 $ \frac{15}{4} $
C.最小值 $ 5 $
D.最小值 $ \frac{15}{4} $
答案:
D[提示:由题意可得6=m²−m,解得m₁=3,m₂=−2.
∵二次函数y=x²+mx+m²−m的图象对称轴在y轴左侧,
∴m >0,
∴m=3,
∴y=x²+3x+6,
∴二次函数有最小值,为$\frac{4ac−b²}{4a}$=$\frac{4×1×6−3²}{4×1}$=$\frac{15}{4}$]
∵二次函数y=x²+mx+m²−m的图象对称轴在y轴左侧,
∴m >0,
∴m=3,
∴y=x²+3x+6,
∴二次函数有最小值,为$\frac{4ac−b²}{4a}$=$\frac{4×1×6−3²}{4×1}$=$\frac{15}{4}$]
3. (2023·四川成都中考)如图,二次函数 $ y = ax^{2} + x - 6 $ 的图象与 $ x $ 轴交于 $ A(-3,0) $,$ B $ 两点,下列说法正确的是 (
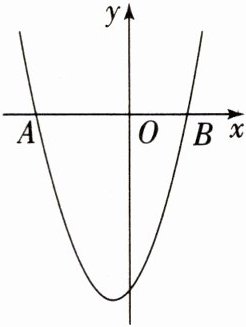
A.抛物线的对称轴为直线 $ x = 1 $
B.抛物线的顶点坐标为 $ (-\frac{1}{2}, -6) $
C.$ A $,$ B $ 两点之间的距离为 $ 5 $
D.当 $ x < -1 $ 时,$ y $ 的值随 $ x $ 值的增大而增大
C
)
A.抛物线的对称轴为直线 $ x = 1 $
B.抛物线的顶点坐标为 $ (-\frac{1}{2}, -6) $
C.$ A $,$ B $ 两点之间的距离为 $ 5 $
D.当 $ x < -1 $ 时,$ y $ 的值随 $ x $ 值的增大而增大
答案:
C[提示:把A(−3,0)代入y=ax²+x−6得0=9a−3−6,解得a=1,
∴y=x²+x−6,对称轴直线为x=−$\frac{b}{2a}$=−$\frac{1}{2}$,故A错误.令y=0,0=x²+x−6,解得x₁=−3,x₂=2,
∴AB =2−(−3)=5,
∴A,B两点之间的距离为5,故C正确.当x=−$\frac{1}{2}$时,y=$\frac{1}{4}$−$\frac{1}{2}$−6=−$\frac{25}{4}$,故B错误.由图象知当x>−$\frac{1}{2}$时,y的值随x值的增大而增大,故D错误.]
∴y=x²+x−6,对称轴直线为x=−$\frac{b}{2a}$=−$\frac{1}{2}$,故A错误.令y=0,0=x²+x−6,解得x₁=−3,x₂=2,
∴AB =2−(−3)=5,
∴A,B两点之间的距离为5,故C正确.当x=−$\frac{1}{2}$时,y=$\frac{1}{4}$−$\frac{1}{2}$−6=−$\frac{25}{4}$,故B错误.由图象知当x>−$\frac{1}{2}$时,y的值随x值的增大而增大,故D错误.]
4. (2023·江苏扬州中考)已知二次函数 $ y = ax^{2} - 2x + \frac{1}{2} $ ( $ a $ 为常数,且 $ a > 0 $),下列结论:①函数图象一定经过第一、二、四象限;②函数图象一定不经过第三象限;③当 $ x < 0 $ 时,$ y $ 随 $ x $ 的增大而减小;④当 $ x > 0 $ 时,$ y $ 随 $ x $ 的增大而增大. 其中所有正确结论的序号是 (
A.①②
B.②③
C.②
D.③④
B
)A.①②
B.②③
C.②
D.③④
答案:
B[提示:
∵a>0时,抛物线开口向上,
∴对称轴为x=$\frac{2}{2a}$=$\frac{1}{a}$>0.当x<0时,y随x的增大而减小;当x>$\frac{1}{a}$时,y随x的增大而增大,
∴函数图象一定不经过第三象限,函数图象可能经过第一、二、四象限.]
∵a>0时,抛物线开口向上,
∴对称轴为x=$\frac{2}{2a}$=$\frac{1}{a}$>0.当x<0时,y随x的增大而减小;当x>$\frac{1}{a}$时,y随x的增大而增大,
∴函数图象一定不经过第三象限,函数图象可能经过第一、二、四象限.]
5. (2023·黑龙江牡丹江中考)将抛物线 $ y = (x + 3)^{2} $ 向下平移 $ 1 $ 个单位长度,再向右平移
2或4
个单位长度后,得到的新抛物线经过原点.
答案:
2或4[提示:抛物线y=(x+3)²向下平移1个单位长度的解析式为y=(x+3)²−1,设抛物线向右平移h个单位长度后,得到的新抛物线经过原点,则新抛物线的解析式为y=(x+3−h)²−1,
∵抛物线经过原点,
∴当x=0时,y=0,
∴(3−h)²−1=0,解得h=2或h=4.]
∵抛物线经过原点,
∴当x=0时,y=0,
∴(3−h)²−1=0,解得h=2或h=4.]
6. (2023·四川达州中考)如图,抛物线 $ y = ax^{2} + bx + c $ ( $ a $,$ b $,$ c $ 为常数)关于直线 $ x = 1 $ 对称. 下列五个结论:① $ abc > 0 $;② $ 2a + b = 0 $;③ $ 4a + 2b + c > 0 $;④ $ am^{2} + bm > a + b $;⑤ $ 3a + c > 0 $. 其中正确的有 (
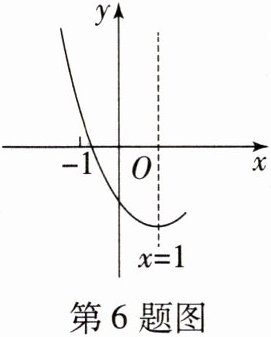
A.$ 4 $ 个
B.$ 3 $ 个
C.$ 2 $ 个
D.$ 1 $ 个
B
)
A.$ 4 $ 个
B.$ 3 $ 个
C.$ 2 $ 个
D.$ 1 $ 个
答案:
B[提示:
∵抛物线y=ax²+bx+c(a,b,c为常数)关于直线x=1对称,
∴−$\frac{b}{2a}$=1.
∵a>0,
∴b=−2a<0.
∵c<0,
∴abc>0,故①正确.由b=−2a,得2a+b=0,故②正确.
∵x=0时,y<0,对称轴为直线x=1,
∴x=2时,y<0,
∴4a +2b+c<0,故③错误.
∵抛物线开口向上,对称轴为直线x =1,
∴am²+bm+c≥a+b+c,即am²+bm≥a+b,故④错误.
∵x=−1时,y>0,
∴a−b+c>0.
∵b=−2a,
∴3a+c >0,故⑤正确.]
∵抛物线y=ax²+bx+c(a,b,c为常数)关于直线x=1对称,
∴−$\frac{b}{2a}$=1.
∵a>0,
∴b=−2a<0.
∵c<0,
∴abc>0,故①正确.由b=−2a,得2a+b=0,故②正确.
∵x=0时,y<0,对称轴为直线x=1,
∴x=2时,y<0,
∴4a +2b+c<0,故③错误.
∵抛物线开口向上,对称轴为直线x =1,
∴am²+bm+c≥a+b+c,即am²+bm≥a+b,故④错误.
∵x=−1时,y>0,
∴a−b+c>0.
∵b=−2a,
∴3a+c >0,故⑤正确.]
7. (2023·辽宁营口中考)如图,抛物线 $ y = ax^{2} + bx + c $ ( $ a \neq 0 $)与 $ x $ 轴交于点 $ A(-3,0) $ 和点 $ B(1,0) $,与 $ y $ 轴交于点 $ C $. 下列说法:① $ abc < 0 $;②抛物线的对称轴为直线 $ x = -1 $;③当 $ -3 < x < 0 $ 时,$ ax^{2} + bx + c > 0 $;④当 $ x > 1 $ 时,$ y $ 随 $ x $ 的增大而增大;⑤ $ am^{2} + bm \leq a - b $ ( $ m $ 为任意实数). 其中正确的有 (
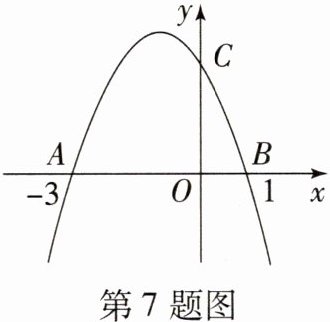
A.$ 1 $ 个
B.$ 2 $ 个
C.$ 3 $ 个
D.$ 4 $ 个
C
)
A.$ 1 $ 个
B.$ 2 $ 个
C.$ 3 $ 个
D.$ 4 $ 个
答案:
C[提示:
∵抛物线开口向下,
∴a<0.
∵抛物线y=ax²+bx +c(a≠0)与x轴交于点A(−3,0)和点B(1,0),
∴对称轴为直线x=$\frac{−3+1}{2}$=−1,故②正确.
∴−$\frac{b}{2a}$=−1,
∴b=2a <0.
∵与y轴的交点在正半轴上,
∴c>0,
∴abc>0,故①错误.由图象知,当−3<x<0时,y>0,
∴当−3<x<0时,ax²+bx+c>0,故③正确.由图象知,当x>1时,y随x的增大而减小,故④错误.
∵抛物线的对称轴为直线x=−1,
∴当x=−1时,函数有最大值,
∴当m为任意实数时,am²+bm +c≤a−b+c,
∴am²+bm≤a−b,故⑤正确.综上,结论正确的是②③⑤.]
∵抛物线开口向下,
∴a<0.
∵抛物线y=ax²+bx +c(a≠0)与x轴交于点A(−3,0)和点B(1,0),
∴对称轴为直线x=$\frac{−3+1}{2}$=−1,故②正确.
∴−$\frac{b}{2a}$=−1,
∴b=2a <0.
∵与y轴的交点在正半轴上,
∴c>0,
∴abc>0,故①错误.由图象知,当−3<x<0时,y>0,
∴当−3<x<0时,ax²+bx+c>0,故③正确.由图象知,当x>1时,y随x的增大而减小,故④错误.
∵抛物线的对称轴为直线x=−1,
∴当x=−1时,函数有最大值,
∴当m为任意实数时,am²+bm +c≤a−b+c,
∴am²+bm≤a−b,故⑤正确.综上,结论正确的是②③⑤.]
8. (2023·黑龙江牡丹江中考)如图,抛物线 $ y = x^{2} + bx + c $ 与 $ x $ 轴交于点 $ A(-1,0) $,$ B(4,0) $,与 $ y $ 轴交于点 $ C $.
(1)求抛物线对应的函数解析式,并直接写出顶点 $ P $ 的坐标;
(2)求 $ \triangle BCP $ 的面积.
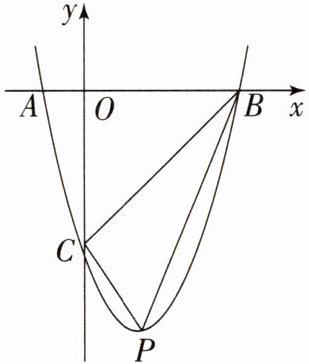
(1)求抛物线对应的函数解析式,并直接写出顶点 $ P $ 的坐标;
(2)求 $ \triangle BCP $ 的面积.

答案:
解:
(1)
∵抛物线y=x²+bx+c与x轴交于点A(−1,0),B(4,0),
∴$\begin{cases}1-b+c=0, \\16+4b+c=0,\end{cases}$解得$\begin{cases}b=-3, \\c=-4,\end{cases}$
∴抛物线的解析式为y=x²-3x-4,
∴P($\frac{3}{2}$,-$\frac{25}{4}$).
(2)如图,连接OP,
∵A(−1,0),B(4,0),C(0,−4),P($\frac{3}{2}$,-$\frac{25}{4}$),
∴S△OPC=$\frac{1}{2}$×4×$\frac{3}{2}$=3,S△BOP=$\frac{1}{2}$×4×$\frac{25}{4}$=$\frac{25}{2}$,S△BOC=$\frac{1}{2}$×4×4=8,
∴S△BPC=S△OPC+S△BOP - S△BOC=3+$\frac{25}{2}$−8=$\frac{15}{2}$.
解:
(1)
∵抛物线y=x²+bx+c与x轴交于点A(−1,0),B(4,0),
∴$\begin{cases}1-b+c=0, \\16+4b+c=0,\end{cases}$解得$\begin{cases}b=-3, \\c=-4,\end{cases}$
∴抛物线的解析式为y=x²-3x-4,
∴P($\frac{3}{2}$,-$\frac{25}{4}$).
(2)如图,连接OP,
∵A(−1,0),B(4,0),C(0,−4),P($\frac{3}{2}$,-$\frac{25}{4}$),
∴S△OPC=$\frac{1}{2}$×4×$\frac{3}{2}$=3,S△BOP=$\frac{1}{2}$×4×$\frac{25}{4}$=$\frac{25}{2}$,S△BOC=$\frac{1}{2}$×4×4=8,
∴S△BPC=S△OPC+S△BOP - S△BOC=3+$\frac{25}{2}$−8=$\frac{15}{2}$.

查看更多完整答案,请扫码查看


