《2025年全科王同步课时练习九年级数学上册人教版》

11. (2023·吉林中考)如图,$AB$,$AC是\odot O$的弦,$OB$,$OC是\odot O$的半径,点$P为OB$上任意一点(点$P不与点B$重合),连接$CP$. 若$\angle BAC = 70^{\circ}$,则$\angle BPC$的度数可能是(D)

A.$70^{\circ}$
B.$105^{\circ}$
C.$125^{\circ}$
D.$155^{\circ}$

答案： D[提示:连接BC，
∵∠BAC=70°,
∴∠BOC=2∠BAC=140°.
∵OB=OC,
∴∠OBC=∠OCB=1/2×(180° - 140°)=20°.
∵点P为OB上任意一点(点P不与点B重合)，
∴0°＜∠OCP＜20°.
∵∠BPC=∠BOC+∠OCP=140°+∠OCP,
∴140°＜∠BPC＜160°.]

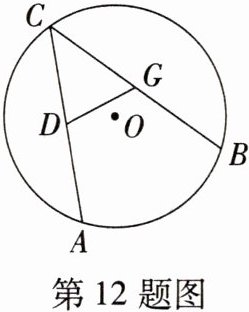
12. (2023·辽宁鞍山中考)如图,$AC$,$BC为\odot O$的两条弦,$D$,$G分别为AC$,$BC$的中点,$\odot O的半径为2$. 若$\angle C = 45^{\circ}$,则$DG$的长为( )

A.$2$
B.$\sqrt{3}$
C.$\frac{3}{2}$
D.$\sqrt{2}$

答案：
D[提示:如图，连接AO,BO,AB，
∵∠C=45°,
∴∠AOB=2∠C=90°.
∵⊙O的半径为2,
∴AO=BO=2,
∴AB=2√2;
∵点D,G分别是AC,BC的中点，
∴DG=1/2AB=√2.

13. 如图,$AB是\odot O$的直径,$C$,$D是\odot O$上的两点,且$BC平分\angle ABD$,$AD分别与BC$,$OC相交于点E$,$F$,则下列结论不一定成立的是(C)

A.$OC// BD$
B.$AD\perp OC$
C.$\triangle CEF\cong\triangle BED$
D.$AF = FD$

答案： C[提示:
∵AB是⊙O的直径，BC平分∠ABD,
∴∠ADB=90°,∠OBC=∠DBC,
∴AD⊥BD.
∵OB=OC,
∴∠OCB=∠OBC,
∴∠DBC=∠OCB,
∴OC//BD,
∴∠AFO=∠ADB =90°,
∴AD⊥OC,
∴AF=FD,选项A,B,D成立.
∵△CEF和△BED中找不到相等的边，
∴△CEF与△BED不一定全等，选项C不成立.]

14. 如图,$AB为\odot O$的直径,点$C$,$D在\odot O$上,$AC与OD交于点E$,$AE = EC$,$OE = ED$. 连接$BC$,$CD$. 求证：
(1) $\triangle AOE\cong\triangle CDE$；
(2) 四边形$OBCD$是菱形.

答案： 证明:
(1)在△AOE和△CDE中,{AE=CE,∠AEO=∠CED,OE=DE},
∴△AOE≌△CDE.　
(2)连接OC,
∵AE=CE,
∴OD⊥AC.
∵OE=DE,
∴CE垂直平分OD,
∴CD=CO,
∴△OCD为等边三角形,
∴∠COD=60°.
∵AB为直径，
∴∠ACB=90°,
∴BC//OD,
∴∠BCO=∠COD=60°.而OB=OC,
∴△OCB为等边三角形,
∴BC=OC,
∴OB=BC=CD=OD,
∴四边形OBCD是菱形.

15. (教材改编题)[2023·湖北武汉中考]如图,$OA$,$OB$,$OC都是\odot O$的半径,$\angle ACB = 2\angle BAC$.
(1) 求证：$\angle AOB = 2\angle BOC$；
(2) 若$AB = 4$,$BC = \sqrt{5}$,求$\odot O$的半径.

答案：

(1)证明:
∵∠ACB=1/2∠AOB,∠BAC=1/2∠BOC,∠ACB=2∠BAC,
∴∠AOB=2∠BOC.　
(2)解:如图，过点O作半径OD⊥AB于点E,连接DB,
∴AE=BE.
∵∠AOB=2∠BOC,∠DOB=1/2∠AOB,
∴∠DOB=∠BOC.
∴BD=BC.
∵AB=4,BC=√5,
∴BE=2,DB=√5.在Rt△BDE中,∠DEB=90°,
∴DE=√(BD² - BE²)=1.在Rt△BOE中,∠OEB=90°,OB²=(OB - 1)²+2²,解得OB=5/2,即⊙O的半径是5/2.

16. (探究题)如图,$\odot C经过原点且与两坐标轴分别交于点A和点B$,点$A的坐标为(0, 2)$,点$B的坐标为(2\sqrt{3}, 0)$,解答下列各题：
(1) 求线段$AB$的长.
(2) 求$\odot C的半径及圆心C$的坐标.
(3) 在$\odot C上是否存在一点P$,使得$\triangle POB$是等腰三角形？若存在,请求出$\angle BOP$的度数；若不存在,请说明理由.

答案：
解:
(1)
∵A(0,2),B(2√3,0),
∴OA=2,OB=2√3;Rt△OAB中，由勾股定理，得AB=√(OA² + OB²)=4.　
(2)如图，
∵∠AOB=90°,
∴AB是⊙C的直径,
∴⊙C的半径r=2.过C作CE⊥y轴于E,则CE//OB.
∵C是AB的中点,
∴CE是△AOB的中位线,则OE=1/2OA=1,CE=1/2OB =√3,即C(√3,1),故⊙C的半径为2,C(√3,1).　
(3)作OB的垂直平分线,交⊙C于P₁,P₂,交OB于D.如图,连接OC,由垂径定理知P₁P₂必过点C,即P₁P₂是⊙C的直径,
∴P₁(√3,3),P₂(√3,-1).在Rt△ODP₁中,P₁D=3,OD=√3,
∴∠BOP₁=60°.
∵P₁P₂是直径,
∴∠P₁OP₂=90°,∠BOP₂=30°.由于P₁P₂垂直平分OB,
∴△OBP₁,△OBP₂都是等腰三角形,因此P₁,P₂均符合P点的要求.由于此时BO=P₁O,因此不需要考虑BO为腰的情况.故存在符合条件的P点:P₁(√3,3),∠BOP₁=60°,P₂(√3,-1),∠BOP₂=30°.