第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
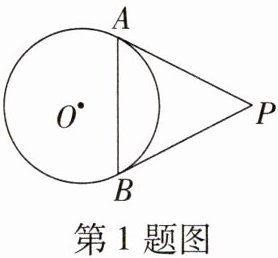
1. 如图,PA,PB与⊙O分别相切于点A,B,PA= 2,∠P= 60°,则AB的长为(
A.$\sqrt{3}$
B.2
C.$2\sqrt{3}$
D.3
B
)
A.$\sqrt{3}$
B.2
C.$2\sqrt{3}$
D.3
答案:
B
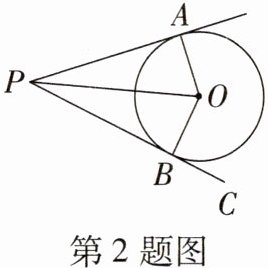
2. 如图,PA,PB是⊙O的切线,且∠APB= 40°,下列说法不正确的是(
A.PA= PB
B.∠APO= 20°
C.∠OBP= 70°
D.∠AOP= 70°
C
)
A.PA= PB
B.∠APO= 20°
C.∠OBP= 70°
D.∠AOP= 70°
答案:
C
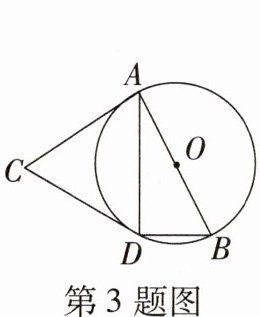
3. (教材改编题)如图,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD= 48°,则∠DBA的大小是(
A.32°
B.48°
C.60°
D.66°
D
)
A.32°
B.48°
C.60°
D.66°
答案:
D[提示:
∵ CA,CD 是⊙O 的切线,
∴ CA = CD.
∵ ∠ACD =48°,
∴ ∠CAD = ∠CDA =66°.
∵ CA ⊥ AB,AB 是直径,
∴ ∠ADB = ∠CAB =90°,
∴ ∠DBA + ∠DAB =90°,∠CAD +∠DAB =90°,
∴ ∠DBA = ∠CAD =66°.
∵ CA,CD 是⊙O 的切线,
∴ CA = CD.
∵ ∠ACD =48°,
∴ ∠CAD = ∠CDA =66°.
∵ CA ⊥ AB,AB 是直径,
∴ ∠ADB = ∠CAB =90°,
∴ ∠DBA + ∠DAB =90°,∠CAD +∠DAB =90°,
∴ ∠DBA = ∠CAD =66°.
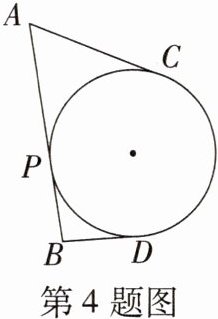
4. 如图,AB,AC,BD是⊙O的切线,P,C,D为切点,如果AB= 8,AC= 5,则BD的长为
3
.
答案:
3[提示:
∵ AC,AP 为⊙O 的切线,
∴ AC = AP.
∵ BP,BD 为⊙O 的切线,
∴ BP = BD,
∴ BD = PB = AB - AP =8 -5 =3.]
∵ AC,AP 为⊙O 的切线,
∴ AC = AP.
∵ BP,BD 为⊙O 的切线,
∴ BP = BD,
∴ BD = PB = AB - AP =8 -5 =3.]
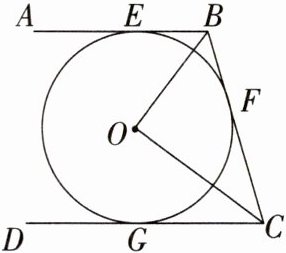
5. (教材改编题)如图,直线AB,BC,CD分别与⊙O相切于点E,F,G,且AB//CD,OB= 6 cm,OC= 8 cm.求:
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
]
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
]

答案:
解:
(1)连接 OF,根据切线长定理得 BE = BF,CF = CG,∠OBF = ∠OBE,∠OCF = ∠OCG.
∵ AB // CD,
∴ ∠ABC +∠BCD =180°,
∴ ∠OBF + ∠OCF =90°,
∴ ∠BOC =90°.
(2)由
(1)知∠BOC =90°.
∵ OB =6 cm,OC =8 cm,
∴ BC =√(OB² + OC²)=10 cm,
∴ BE + CG = BC =10 cm.
(3)
∵ OF⊥BC,
∴ S△OBC = (1/2)OF·BC = (1/2)OB·OC,即 (1/2)OF×10 =(1/2)×6×8.
∴ 半径 OF =4.8 cm.
(1)连接 OF,根据切线长定理得 BE = BF,CF = CG,∠OBF = ∠OBE,∠OCF = ∠OCG.
∵ AB // CD,
∴ ∠ABC +∠BCD =180°,
∴ ∠OBF + ∠OCF =90°,
∴ ∠BOC =90°.
(2)由
(1)知∠BOC =90°.
∵ OB =6 cm,OC =8 cm,
∴ BC =√(OB² + OC²)=10 cm,
∴ BE + CG = BC =10 cm.
(3)
∵ OF⊥BC,
∴ S△OBC = (1/2)OF·BC = (1/2)OB·OC,即 (1/2)OF×10 =(1/2)×6×8.
∴ 半径 OF =4.8 cm.
6. 下面关于“三角形的内心”说法正确的是(
A.三角形的内心到三边的距离相等
B.三角形的内心是三边垂直平分线的交点
C.三角形的内心是三边中线的交点
D.三角形的内心到三个顶点的距离相等
A
)A.三角形的内心到三边的距离相等
B.三角形的内心是三边垂直平分线的交点
C.三角形的内心是三边中线的交点
D.三角形的内心到三个顶点的距离相等
答案:
A
7. (教材改编题)如图,△ABC中,∠A= 80°,点O是△ABC的内心,则∠BOC的度数为(
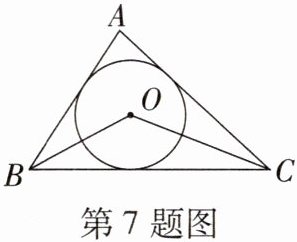
A.100°
B.160°
C.80°
D.130°
D
)
A.100°
B.160°
C.80°
D.130°
答案:
D[提示:
∵ ∠A =80°,
∴ ∠ABC + ∠ACB =180° - ∠A =100°.
∵ 点 O 是△ABC 的内心,
∴ ∠OBC + ∠OCB =(1/2)(∠ABC + ∠ACB)=50°,
∴ ∠BOC =180° -50° =130°.
∵ ∠A =80°,
∴ ∠ABC + ∠ACB =180° - ∠A =100°.
∵ 点 O 是△ABC 的内心,
∴ ∠OBC + ∠OCB =(1/2)(∠ABC + ∠ACB)=50°,
∴ ∠BOC =180° -50° =130°.
8. (数学文化)[2023·江苏镇江中考]《九章算术》中记载:“今有勾八步,股一十五步.问勾中容圆径几何?”译文:今有一个直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形内切圆的直径是多少?书中给出的算法译文如下:如图,根据勾、股,求得弦长.用勾、股、弦相加作为除数,用勾乘以股,再乘以2作为被除数,商即为该直角三角形内切圆的直径,则该直径等于
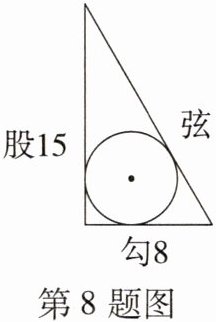
6
步(注:“步”为长度单位).
答案:
6[提示:根据勾股定理得斜边为√(8² +15²)=17,则该直角三角形能容纳的圆形(内切圆)半径 r=(8 +15 -17)/2=3(步),即直径为6步.]
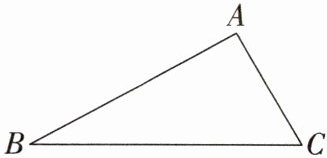
9. 如图,已知△ABC,∠B= 40°.
(1)在图中,用尺规作出△ABC的内切圆O,并标出⊙O与边AB,BC,AC的切点D,E,F(保留痕迹,不必写作法);
(2)连接EF,DF,求∠EFD的度数.
]
(1)在图中,用尺规作出△ABC的内切圆O,并标出⊙O与边AB,BC,AC的切点D,E,F(保留痕迹,不必写作法);
(2)连接EF,DF,求∠EFD的度数.
]

答案:
解:
(1)如图,⊙O 为所作.
(2)连接 OD,
∵ ⊙O 与边 AB,BC 相切,
∴ OD ⊥ AB,OE ⊥ BC,
∴ ∠ODB =∠OEB =90°,
∴ ∠DOE =180° -∠ABC =180° -40° =140°,
∴ ∠EFD=(1/2)∠DOE =70°.

解:
(1)如图,⊙O 为所作.
(2)连接 OD,
∵ ⊙O 与边 AB,BC 相切,
∴ OD ⊥ AB,OE ⊥ BC,
∴ ∠ODB =∠OEB =90°,
∴ ∠DOE =180° -∠ABC =180° -40° =140°,
∴ ∠EFD=(1/2)∠DOE =70°.

查看更多完整答案,请扫码查看


