第38页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
11. 甲、乙、丙三名同学每人抽取一张卡片,每张卡片上有一个形如 $ y = ax^{2} + bx $ 的二次函数的解析式,其中只有一人与其他两人抽到的解析式不同。下面是他们对抽到的解析式所对应的图象的描述:甲:开口向下;乙:顶点在第三象限;丙:经过点 $ (-2, 0) $,$ (1, 3) $。根据描述可知,抽到与其他两人解析式不同的是(
A.甲
B.乙
C.丙
D.都有可能
A
)A.甲
B.乙
C.丙
D.都有可能
答案:
A[提示:
∵抛物线y = ax² + bx经过原点,
∴当开口向下时,顶点不可能在第三象限,
∴甲、乙的解析式不同.当开口向下时,图象过(-2,0),(0,0),则抛物线不可能经过(1,3),
∴甲、丙的解析式不同,
∴抽到与其他两人解析式不同的是甲.]
∵抛物线y = ax² + bx经过原点,
∴当开口向下时,顶点不可能在第三象限,
∴甲、乙的解析式不同.当开口向下时,图象过(-2,0),(0,0),则抛物线不可能经过(1,3),
∴甲、丙的解析式不同,
∴抽到与其他两人解析式不同的是甲.]
12. 如图,平行四边形 $ ABCD $ 中,$ AB = 4 $,点 $ D $ 的坐标是 $ (0, 8) $,以点 $ C $ 为顶点的抛物线经过 $ x $ 轴上的点 $ A $,$ B $,则此抛物线的解析式为 。
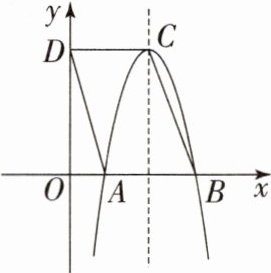

答案:
y = -2x² + 16x - 24[提示:在平行四边形ABCD中,CD//AB且CD = AB = 4,点D的坐标是(0,8),
∴点C的坐标为(4,8).如图,设抛物线的对称轴与x轴相交于点H,则AH = BH = 2,
∴点A,B的坐标为A(2,0),B(6,0),C(4,8).设抛物线的解析式为y = a(x - 4)² + 8,把A(2,0)代入,得0 = 4a + 8,解得a = -2,
∴y = -2(x - 4)² + 8,
∴抛物线的解析式为y = -2x² + 16x - 24.]

y = -2x² + 16x - 24[提示:在平行四边形ABCD中,CD//AB且CD = AB = 4,点D的坐标是(0,8),
∴点C的坐标为(4,8).如图,设抛物线的对称轴与x轴相交于点H,则AH = BH = 2,
∴点A,B的坐标为A(2,0),B(6,0),C(4,8).设抛物线的解析式为y = a(x - 4)² + 8,把A(2,0)代入,得0 = 4a + 8,解得a = -2,
∴y = -2(x - 4)² + 8,
∴抛物线的解析式为y = -2x² + 16x - 24.]

13. (2023·吉林长春二道区模拟)如图,已知平面直角坐标系中的四个点:$ A(0, 2) $,$ B(1, 0) $,$ C(3, 1) $,$ D(2, 3) $。二次函数 $ y = ax^{2} + bx + c $ 的图象经过其中任意三个点,当 $ a $ 的值最大时,二次函数的解析式为

y = $\frac{5}{2}$x² - $\frac{9}{2}$x + 2
。
答案:
y = $\frac{5}{2}$x² - $\frac{9}{2}$x + 2[提示:由图象知A,B,D组成的抛物线开口向上,a > 0.A,B,C组成的抛物线开口向上,a > 0.B,C,D三点组成的抛物线开口向下,a < 0.A,D,C三点组成的抛物线开口向下,a < 0.
∵A,B,D组成的二次函数的图象的开口小于A,B,C组成的二次函数的图象开口,
∴A,B,D组成的二次函数的图象中,a的值最大.当抛物线y = ax² + bx + c过A,B,D三点时,则{c = 2,a + b + c = 0,4a + 2b + c = 3},解得{a = $\frac{5}{2}$,b = -$\frac{9}{2}$,c = 2},故a的值最大时,二次函数的解析式为y = $\frac{5}{2}$x² - $\frac{9}{2}$x + 2.]
∵A,B,D组成的二次函数的图象的开口小于A,B,C组成的二次函数的图象开口,
∴A,B,D组成的二次函数的图象中,a的值最大.当抛物线y = ax² + bx + c过A,B,D三点时,则{c = 2,a + b + c = 0,4a + 2b + c = 3},解得{a = $\frac{5}{2}$,b = -$\frac{9}{2}$,c = 2},故a的值最大时,二次函数的解析式为y = $\frac{5}{2}$x² - $\frac{9}{2}$x + 2.]
14. (2023·浙江绍兴中考)已知二次函数 $ y = -x^{2} + bx + c $。
(1)当 $ b = 4 $,$ c = 3 $ 时,
①求该函数图象的顶点坐标;
②当 $ -1 \leq x \leq 3 $ 时,求 $ y $ 的取值范围。
(2)当 $ x \leq 0 $ 时,$ y $ 的最大值为 $ 2 $;当 $ x > 0 $ 时,$ y $ 的最大值为 $ 3 $,求二次函数的解析式。
(1)当 $ b = 4 $,$ c = 3 $ 时,
①求该函数图象的顶点坐标;
②当 $ -1 \leq x \leq 3 $ 时,求 $ y $ 的取值范围。
(2)当 $ x \leq 0 $ 时,$ y $ 的最大值为 $ 2 $;当 $ x > 0 $ 时,$ y $ 的最大值为 $ 3 $,求二次函数的解析式。
答案:
解:
(1)①
∵b = 4,c = 3,
∴y = -x² + 4x + 3 = -(x - 2)² + 7,
∴顶点坐标为(2,7).②
∵-1 ≤ x ≤ 3中含有顶点(2,7),
∴当x = 2时,y有最大值7.
∵2 - (-1) > 3 - 2,
∴当x = -1时,y有最小值 - 2,
∴当 - 1 ≤ x ≤ 3时,-2 ≤ y ≤ 7.
(2)
∵x ≤ 0时,y的最大值为2,x > 0时,y的最大值为3,
∴抛物线的对称轴为x = $\frac{b}{2}$,在y轴的右侧,
∴b > 0.
∵抛物线开口向下,x ≤ 0时,y的最大值为2,
∴c = 2.又
∵[4×(-1)×c - b²]/[4×(-1)] = 3,
∴b = ±2.
∵b > 0,
∴b = 2,
∴二次函数的解析式为y = -x² + 2x + 2.
(1)①
∵b = 4,c = 3,
∴y = -x² + 4x + 3 = -(x - 2)² + 7,
∴顶点坐标为(2,7).②
∵-1 ≤ x ≤ 3中含有顶点(2,7),
∴当x = 2时,y有最大值7.
∵2 - (-1) > 3 - 2,
∴当x = -1时,y有最小值 - 2,
∴当 - 1 ≤ x ≤ 3时,-2 ≤ y ≤ 7.
(2)
∵x ≤ 0时,y的最大值为2,x > 0时,y的最大值为3,
∴抛物线的对称轴为x = $\frac{b}{2}$,在y轴的右侧,
∴b > 0.
∵抛物线开口向下,x ≤ 0时,y的最大值为2,
∴c = 2.又
∵[4×(-1)×c - b²]/[4×(-1)] = 3,
∴b = ±2.
∵b > 0,
∴b = 2,
∴二次函数的解析式为y = -x² + 2x + 2.
15. (情境题)如图,在一条笔直的滑道上有黑、白两个小球同向运动,黑球在 $ A $ 处开始减速,此时白球在黑球前面 $ 70 \mathrm{cm} $ 处。

小聪测量黑球减速后的运动速度 $ v $(单位:$ \mathrm{cm/s} $)、运动距离 $ y $(单位:$ \mathrm{cm} $)随运动时间 $ t $(单位:$ \mathrm{s} $)变化的数据,整理得下表。
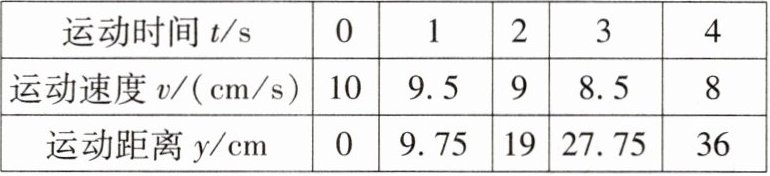
小聪探究发现,黑球的运动速度 $ v $ 与运动时间 $ t $ 之间成一次函数关系,运动距离 $ y $ 与运动时间 $ t $ 之间成二次函数关系。
(1)直接写出 $ v $ 关于 $ t $ 的函数解析式和 $ y $ 关于 $ t $ 的函数解析式(不要求写出自变量的取值范围);
(2)当黑球减速后运动距离为 $ 64 \mathrm{cm} $ 时,求它此时的运动速度;
(3)若白球一直以 $ 2 \mathrm{cm/s} $ 的速度匀速运动,则黑球在运动过程中会不会碰到白球?请说明理由。

小聪测量黑球减速后的运动速度 $ v $(单位:$ \mathrm{cm/s} $)、运动距离 $ y $(单位:$ \mathrm{cm} $)随运动时间 $ t $(单位:$ \mathrm{s} $)变化的数据,整理得下表。

小聪探究发现,黑球的运动速度 $ v $ 与运动时间 $ t $ 之间成一次函数关系,运动距离 $ y $ 与运动时间 $ t $ 之间成二次函数关系。
(1)直接写出 $ v $ 关于 $ t $ 的函数解析式和 $ y $ 关于 $ t $ 的函数解析式(不要求写出自变量的取值范围);
(2)当黑球减速后运动距离为 $ 64 \mathrm{cm} $ 时,求它此时的运动速度;
(3)若白球一直以 $ 2 \mathrm{cm/s} $ 的速度匀速运动,则黑球在运动过程中会不会碰到白球?请说明理由。
答案:
解:
(1)设v = mt + n,将(0,10),(2,9)代入,得{n = 10,2m + n = 9},解得{m = -$\frac{1}{2}$,n = 10},
∴v = -$\frac{1}{2}$t + 10.设y = at² + bt + c,将(0,0),(2,19),(4,36)代入,得{c = 0,4a + 2b + c = 19,16a + 4b + c = 36},解得{a = -$\frac{1}{4}$,b = 10,c = 0},
∴y = -$\frac{1}{4}$t² + 10t.
(2)令y = 64,即 - $\frac{1}{4}$t² + 10t = 64,解得t = 8或t = 32,当t = 8时,v = 6;当t = 32时,v = -6(舍).
(3)设黑白两球的距离为w cm,根据题意知w = 70 + 2t - y = $\frac{1}{4}$t² - 8t + 70 = $\frac{1}{4}$(t - 16)² + 6,
∵$\frac{1}{4}$ > 0,
∴当t = 16时,w的最小值为6,
∴黑白两球的最小距离为6 cm,大于0,黑球不会碰到白球.
(1)设v = mt + n,将(0,10),(2,9)代入,得{n = 10,2m + n = 9},解得{m = -$\frac{1}{2}$,n = 10},
∴v = -$\frac{1}{2}$t + 10.设y = at² + bt + c,将(0,0),(2,19),(4,36)代入,得{c = 0,4a + 2b + c = 19,16a + 4b + c = 36},解得{a = -$\frac{1}{4}$,b = 10,c = 0},
∴y = -$\frac{1}{4}$t² + 10t.
(2)令y = 64,即 - $\frac{1}{4}$t² + 10t = 64,解得t = 8或t = 32,当t = 8时,v = 6;当t = 32时,v = -6(舍).
(3)设黑白两球的距离为w cm,根据题意知w = 70 + 2t - y = $\frac{1}{4}$t² - 8t + 70 = $\frac{1}{4}$(t - 16)² + 6,
∵$\frac{1}{4}$ > 0,
∴当t = 16时,w的最小值为6,
∴黑白两球的最小距离为6 cm,大于0,黑球不会碰到白球.
查看更多完整答案,请扫码查看


