第84页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
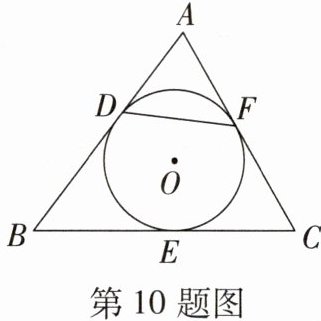
10. 如图,△ABC中,∠A= 60°,BC= 6,它的周长为16.若⊙O与BC,AC,AB三边分别切于点E,F,D,则DF的长为(
A.2
B.3
C.4
D.6
2
)
A.2
B.3
C.4
D.6
答案:
A[提示:
∵ ⊙O 与 BC,AC,AB 三边分别切于点 E,F,D,
∴ AD = AF,BE = BD,CE = CF.
∵ BC = BE + CE =6,
∴ BD +CF =6.
∵ AD = AF,∠A =60°,
∴ △ADF 是等边三角形,
∴ AD = AF = DF.
∵ AB + AC + BC =16,BC =6,
∴ AB + AC =10.
∵ BD + CF =6,
∴ AD + AF =4.
∵ AD = AF = DF,
∴ DF=AF = AD=(1/2)×4=2.]
∵ ⊙O 与 BC,AC,AB 三边分别切于点 E,F,D,
∴ AD = AF,BE = BD,CE = CF.
∵ BC = BE + CE =6,
∴ BD +CF =6.
∵ AD = AF,∠A =60°,
∴ △ADF 是等边三角形,
∴ AD = AF = DF.
∵ AB + AC + BC =16,BC =6,
∴ AB + AC =10.
∵ BD + CF =6,
∴ AD + AF =4.
∵ AD = AF = DF,
∴ DF=AF = AD=(1/2)×4=2.]
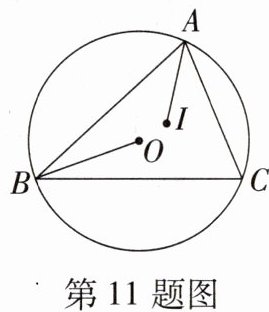
11. (2023·山东聊城中考)如图,点O是△ABC外接圆的圆心,点I是△ABC的内心,连接OB,IA.若∠CAI= 35°,则∠OBC的度数为(
A.15°
B.17.5°
C.20°
D.25°
C
)
A.15°
B.17.5°
C.20°
D.25°
答案:
C[提示:连接 OC,
∵ 点 I 是△ABC 的内心,
∴ AI 平分∠BAC.
∵ ∠CAI =35°,
∴ ∠BAC =2∠CAI =70°.
∵ 点 O 是△ABC 外接圆的圆心,
∴ ∠BOC =2∠BAC =140°.
∵ OB =OC,
∴ ∠OBC = ∠OCB=(1/2)×(180° - ∠BOC)=(1/2)×(180° -140°)=20°.]
∵ 点 I 是△ABC 的内心,
∴ AI 平分∠BAC.
∵ ∠CAI =35°,
∴ ∠BAC =2∠CAI =70°.
∵ 点 O 是△ABC 外接圆的圆心,
∴ ∠BOC =2∠BAC =140°.
∵ OB =OC,
∴ ∠OBC = ∠OCB=(1/2)×(180° - ∠BOC)=(1/2)×(180° -140°)=20°.]
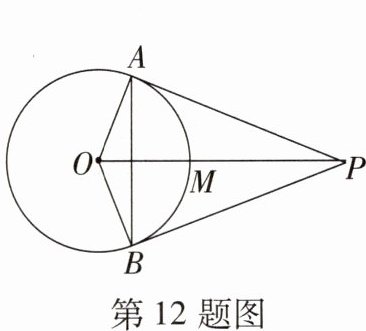
12. 如图,已知PA,PB是⊙O的两条切线,A,B为切点,线段OP交⊙O于点M.给出下列四种说法:①PA= PB;②OP⊥AB;③四边形OAPB有外接圆;④M是△AOP外接圆的圆心.其中正确说法的个数是(
A.1
B.2
C.3
D.4
C
)
A.1
B.2
C.3
D.4
答案:
C[提示:
∵ PA,PB 是⊙O 的两条切线,A,B 为切点,
∴ PA= PB,
∴ ①正确.
∵ OA = OB,PA = PB,
∴ OP 垂直平分 AB,
∴ ②正确.
∵ PA,PB 是⊙O 的两条切线,A,B 为切点,
∴ OA⊥PA,OB⊥PB,
∴ ∠OAP = ∠OBP =90°,
∴ 点 A,B 在以OP 为直径的圆上,
∴ 四边形 OAPB 有外接圆,
∴ ③正确.
∵ 只有当∠APO =30°时,OP =2OA,此时 PM = OM,
∴ M 不一定为△AOP 外接圆的圆心,
∴ ④错误.]
∵ PA,PB 是⊙O 的两条切线,A,B 为切点,
∴ PA= PB,
∴ ①正确.
∵ OA = OB,PA = PB,
∴ OP 垂直平分 AB,
∴ ②正确.
∵ PA,PB 是⊙O 的两条切线,A,B 为切点,
∴ OA⊥PA,OB⊥PB,
∴ ∠OAP = ∠OBP =90°,
∴ 点 A,B 在以OP 为直径的圆上,
∴ 四边形 OAPB 有外接圆,
∴ ③正确.
∵ 只有当∠APO =30°时,OP =2OA,此时 PM = OM,
∴ M 不一定为△AOP 外接圆的圆心,
∴ ④错误.]
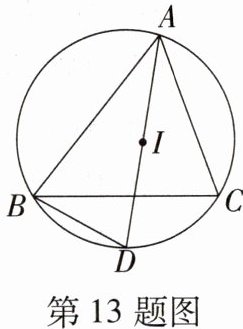
13. 如图,△ABC的内心为I,连接AI并延长交△ABC的外接圆于D,则线段DI与DB的关系是( )
A.DI= DB
B.DI>DB
C.DI<DB
D.不确定

A.DI= DB
B.DI>DB
C.DI<DB
D.不确定
答案:
A[提示:连接 BI,如图,
∵ △ABC 的内心为 I,
∴ ∠1 = ∠2,∠5 = ∠6.
∵ ∠3 = ∠1,
∴ ∠3 = ∠2.
∵ ∠4 = ∠2 + ∠6 =∠3 + ∠5,即∠4 = ∠DBI,
∴ DI = DB.]

A[提示:连接 BI,如图,
∵ △ABC 的内心为 I,
∴ ∠1 = ∠2,∠5 = ∠6.
∵ ∠3 = ∠1,
∴ ∠3 = ∠2.
∵ ∠4 = ∠2 + ∠6 =∠3 + ∠5,即∠4 = ∠DBI,
∴ DI = DB.]

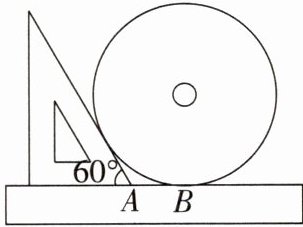
14. (2023·山东泰安中考)为了测量一个圆形光盘的半径,小明把直尺、光盘和三角尺按如图所示放置于桌面上,并量出AB= 4 cm,则这张光盘的半径是______ cm.(精确到0.1 cm.参考数据:$\sqrt{3}\approx1.73$)
]
]

答案:
6.9[提示:设光盘的圆心为 O,由题意知 AB,AC 切⊙O 于C,B,连接 OC,OB,OA,如图,
∵ AC,AB 分别为⊙O 的切线,
∴ AO 为∠CAB 的平分线,OC ⊥ AC,OB ⊥ AB.又∠CAD =60°,
∴ ∠OAC = ∠OAB=(1/2)∠CAB =60°.在 Rt△AOB 中,∠OAB =60°,AB =4,
∴ ∠AOB =30°,
∴ OA =2AB =8,
∴ OB=√(OA² - AB²)=√(8² -4²)=4√3≈6.9,即这张光盘的半径约为6.9 cm.]

6.9[提示:设光盘的圆心为 O,由题意知 AB,AC 切⊙O 于C,B,连接 OC,OB,OA,如图,
∵ AC,AB 分别为⊙O 的切线,
∴ AO 为∠CAB 的平分线,OC ⊥ AC,OB ⊥ AB.又∠CAD =60°,
∴ ∠OAC = ∠OAB=(1/2)∠CAB =60°.在 Rt△AOB 中,∠OAB =60°,AB =4,
∴ ∠AOB =30°,
∴ OA =2AB =8,
∴ OB=√(OA² - AB²)=√(8² -4²)=4√3≈6.9,即这张光盘的半径约为6.9 cm.]

15. 如图,PA,PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB= 60°.求:
(1)PA的长;
(2)∠COD的度数.
]
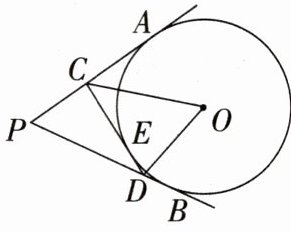
(1)PA的长;
(2)∠COD的度数.
]

答案:
解:
(1)
∵ CA,CE 都是圆 O 的切线,
∴ CA = CE,同理 DE =DB,PA = PB,
∴ △PCD 的周长 = PD + CD + PC = PD + PC+ CA + BD = PA + PB =2PA =12,即 PA 的长为 6.
(2)
∵ ∠P =60°,
∴ ∠PCE + ∠PDE =120°,
∴ ∠ACD +∠CDB =360° -120° =240°.
∵ CA,CE 是圆 O 的切线,
∴ ∠OCE = ∠OCA=(1/2)∠ACD.同理∠ODE=(1/2)∠CDB,
∴ ∠OCE + ∠ODE=(1/2)(∠ACD + ∠CDB)=120°,
∴ ∠COD =180° -120° =60°.
(1)
∵ CA,CE 都是圆 O 的切线,
∴ CA = CE,同理 DE =DB,PA = PB,
∴ △PCD 的周长 = PD + CD + PC = PD + PC+ CA + BD = PA + PB =2PA =12,即 PA 的长为 6.
(2)
∵ ∠P =60°,
∴ ∠PCE + ∠PDE =120°,
∴ ∠ACD +∠CDB =360° -120° =240°.
∵ CA,CE 是圆 O 的切线,
∴ ∠OCE = ∠OCA=(1/2)∠ACD.同理∠ODE=(1/2)∠CDB,
∴ ∠OCE + ∠ODE=(1/2)(∠ACD + ∠CDB)=120°,
∴ ∠COD =180° -120° =60°.
16. 【问题引入】古希腊几何学家海伦和我国南宋数学家秦九韶都曾提出利用三角形的三边求面积的公式,为海伦—秦九韶公式,如果一个三角形的三边长分别是a,b,c,记$p= \frac{a+b+c}{2}$,那么三角形面积为:$S= \sqrt{p(p - a)(p - b)(p - c)}$,在△ABC中,∠A,∠B,∠C所对的边长分别为a,b,c,若a= 3,b= 4,c= 5,则△ABC的面积为6.
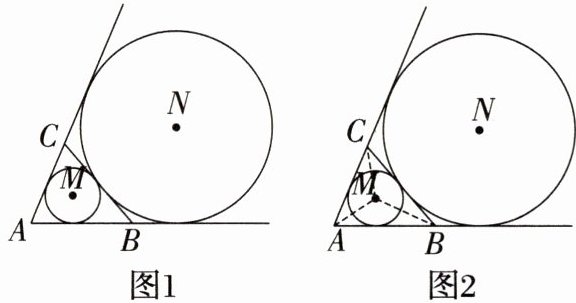
【问题探索】如图1,在△ABC中,设BC= a,AC= b,AB= c,$p= \frac{a+b+c}{2}$,⊙M是△ABC的内切圆,⊙N分别与AC的延长线、AB的延长线以及线段BC均只有一个公共点,⊙M的半径为m,⊙N的半径为n.
(1)分析与证明:如图2,连接MA,MB,MC,则△ABC被划分为三个小三角形,用S表示△ABC的面积,即$S = S_{△MBC} + S_{△MCA} + S_{△MAB}$,那么S= ______;
(2)理解与应用:当∠A= 60°,m= 2,n= 6时,△ABC的面积为______.
]
【问题探索】如图1,在△ABC中,设BC= a,AC= b,AB= c,$p= \frac{a+b+c}{2}$,⊙M是△ABC的内切圆,⊙N分别与AC的延长线、AB的延长线以及线段BC均只有一个公共点,⊙M的半径为m,⊙N的半径为n.
(1)分析与证明:如图2,连接MA,MB,MC,则△ABC被划分为三个小三角形,用S表示△ABC的面积,即$S = S_{△MBC} + S_{△MCA} + S_{△MAB}$,那么S= ______;
(2)理解与应用:当∠A= 60°,m= 2,n= 6时,△ABC的面积为______.
]

答案:
(1)pm
(2)12√3[提示:
(1)如图,S = p·m 成立,理由如下:S = S△MBC + S△MCA + S△MAB=(am)/2 + (bm)/2 + (cm)/2=(a + b + c)/2·m.又
∵ p=(a + b + c)/2,
∴ S = pm.
(2)如图,过点 N 分别作 AB,CB,AC 的垂线,垂足分别为点 D,E,F,
∵ ⊙N 分别与 AC 的延长线、AB 的延长线以及线段 BC 均只有一个公共点,
∴ AD,AF,BC 与⊙N 分别相切于点 D,F,E,
∴ AD = AF,CF = CE,BE = BD,
∴ AD = AF=(1/2)(AD + AF)=(1/2)(AB + BD + AC +CF)=(1/2)(AB + BE + AC + CE)=(1/2)(AB + BC + CA)= p.
∵ ND ⊥ AB,NF ⊥ AC,
∴ AN 平分∠CAB,
∴ ∠NAD=(1/2)∠CAB=30°.在 Rt△ADN 中,DN =6,∠NAD =30°,
∴ AD =√3 ND=6√3 = p,
∴ S△ABC = pm =6√3×2 =12√3.]

(1)pm
(2)12√3[提示:
(1)如图,S = p·m 成立,理由如下:S = S△MBC + S△MCA + S△MAB=(am)/2 + (bm)/2 + (cm)/2=(a + b + c)/2·m.又
∵ p=(a + b + c)/2,
∴ S = pm.
(2)如图,过点 N 分别作 AB,CB,AC 的垂线,垂足分别为点 D,E,F,
∵ ⊙N 分别与 AC 的延长线、AB 的延长线以及线段 BC 均只有一个公共点,
∴ AD,AF,BC 与⊙N 分别相切于点 D,F,E,
∴ AD = AF,CF = CE,BE = BD,
∴ AD = AF=(1/2)(AD + AF)=(1/2)(AB + BD + AC +CF)=(1/2)(AB + BE + AC + CE)=(1/2)(AB + BC + CA)= p.
∵ ND ⊥ AB,NF ⊥ AC,
∴ AN 平分∠CAB,
∴ ∠NAD=(1/2)∠CAB=30°.在 Rt△ADN 中,DN =6,∠NAD =30°,
∴ AD =√3 ND=6√3 = p,
∴ S△ABC = pm =6√3×2 =12√3.]

查看更多完整答案,请扫码查看


