第9页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
7.若长方体从一个顶点发出的三条棱长分
别为2,3,4,则该长方体的表面积为
别为2,3,4,则该长方体的表面积为
52
,体积为24
。
答案:
7.52 24
8.[数学应用]某班数学活动小组的同学们
用纸板制作长方体包装盒,其表面展开
图和相关尺寸(单位:mm)如下,其中阴
影部分为内部粘贴角料,求此长方体包
装盒的体积。

用纸板制作长方体包装盒,其表面展开
图和相关尺寸(单位:mm)如下,其中阴
影部分为内部粘贴角料,求此长方体包
装盒的体积。

答案:
8.解:由题意,知此长方体的长为70 mm,宽为65 mm,高为40 mm,
则此长方体包装盒的体积为$70 × 65 × 40 = 182000(mm^3)$。
则此长方体包装盒的体积为$70 × 65 × 40 = 182000(mm^3)$。
9.如图所示的长方形是圆柱的侧面展开
图,已知这个长方形相邻的两边长分别
为6,4π,求圆柱的体积。
课堂延伸.提升素养
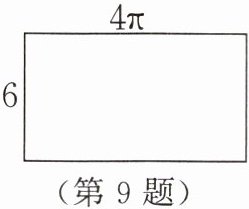
图,已知这个长方形相邻的两边长分别
为6,4π,求圆柱的体积。
课堂延伸.提升素养

答案:
9.解:①以$4 \pi$为底面周长,6为高,
此时圆柱的底面半径为$\frac{4 \pi}{2 \pi} = 2$,
所以圆柱的体积为$\pi × 2^2 × 6 = 24 \pi$。
②以6为圆柱的底面周长,$4 \pi$为高,
此时圆柱的底面半径为$\frac{6}{2 \pi} = \frac{3}{\pi}$,
所以圆柱的体积为$\pi × (\frac{3}{\pi})^2 × 4 \pi = 36$。
所以圆柱的体积为$24 \pi$或36。
此时圆柱的底面半径为$\frac{4 \pi}{2 \pi} = 2$,
所以圆柱的体积为$\pi × 2^2 × 6 = 24 \pi$。
②以6为圆柱的底面周长,$4 \pi$为高,
此时圆柱的底面半径为$\frac{6}{2 \pi} = \frac{3}{\pi}$,
所以圆柱的体积为$\pi × (\frac{3}{\pi})^2 × 4 \pi = 36$。
所以圆柱的体积为$24 \pi$或36。
10.[综合与实践]如图所示的是长方体的
表面展开图,将其折叠成一个长方体。
(1)和数字1所在的面相对的面是哪个
数字所在的面?
(2)若FG=3cm,LK=8cm,EI=
18cm,则该长方体的表面积和体积分
别是多少?

表面展开图,将其折叠成一个长方体。
(1)和数字1所在的面相对的面是哪个
数字所在的面?
(2)若FG=3cm,LK=8cm,EI=
18cm,则该长方体的表面积和体积分
别是多少?

答案:
10.解:
(1)和数字1所在的面相对的面是数字3所在的面。
(2)$DI = EI - ED = EI - FG = 18 - 3 = 15(cm)$。
表面积:$(3 × 8 + 3 × 15 + 8 × 15) × 2 = 378(cm^2)$,
体积:$3 × 8 × 15 = 360(cm^3)$。
(1)和数字1所在的面相对的面是数字3所在的面。
(2)$DI = EI - ED = EI - FG = 18 - 3 = 15(cm)$。
表面积:$(3 × 8 + 3 × 15 + 8 × 15) × 2 = 378(cm^2)$,
体积:$3 × 8 × 15 = 360(cm^3)$。
查看更多完整答案,请扫码查看


