《2025年课堂精练七年级数学上册北师大版双色版》

11. 试说明不论$x$取何值，代数式$(x^{3}+5x^{2}+4x-3)-(-x^{2}+2x^{3}-3x-1)+(4-7x-6x^{2}+x^{3})$的值不变。

答案： 11.解：因为原式$=x^{3}+5x^{2}+4x-3+x^{2}-2x^{3}+3x+1+4-7x-6x^{2}+x^{3}=(1-2+1)x^{3}+(5+1-6)x^{2}+(4+3-7)x+(-3+1+4)=2，$
所以不论x取何值，代数式$(x^{3}+5x^{2}+4x-3)-(-x^{2}+2x^{3}-3x-1)+(4-7x-6x^{2}+x^{3})$的值不变。

12. 已知关于$x,y$的多项式$5x^{2}-2xy^{2}-[3xy+4y^{2}+(9xy-2y^{2}-2mxy^{2})+7x^{2}]-1$。
(1)若该多项式不含三次项，求$m$的值；
(2)在(1)的条件下，当$x^{2}+y^{2}=13$，$xy=-6$时，求该多项式的值。

答案： 12.解：
(1)原式$=-2x^{2}-2y^{2}-12xy+(-2+2m)xy^{2}-1。$
因为该多项式不含三次项，所以-2+2m=0，
解得m=1。
(2)原式$=-2x^{2}-2y^{2}-12xy-1=-2(x^{2}+y^{2})-12xy-1。$
当$x^{2}+y^{2}=13,xy=-6$时，
原式$=-2(x^{2}+y^{2})-12xy-1=-2×13-12×(-6)-1=45。$

13. 由于看错了符号，某学生把一个代数式减$-4a^{2}+2b^{2}+3c^{2}$误认为加$-4a^{2}+2b^{2}+3c^{2}$，结果得出的答案是$a^{2}-4b^{2}-2c^{2}$，求原题的正确答案。

答案： 13.解：原代数式$=(a^{2}-4b^{2}-2c^{2})-(-4a^{2}+2b^{2}+3c^{2})=a^{2}-4b^{2}-2c^{2}+4a^{2}-2b^{2}-3c^{2}=5a^{2}-6b^{2}-5c^{2}。$
所以原题的正确答案是$(5a^{2}-6b^{2}-5c^{2})-(-4a^{2}+2b^{2}+3c^{2})=5a^{2}-6b^{2}-5c^{2}+4a^{2}-2b^{2}-3c^{2}=9a^{2}-8b^{2}-8c^{2}。$

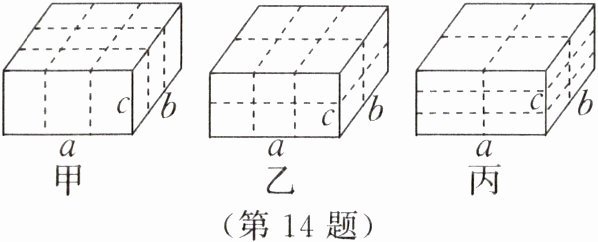
14. 【数学应用】有一个长方体形状的物体，它的长、宽、高分别为$a,b,c(a＞b＞c)$。现有三种不同的捆扎方式(如图所示的虚线)，哪种方式用绳最少？哪种方式用绳最多？请说明理由。
]

答案： 14.解：甲种方式用绳最少，丙种方式用绳最多。
理由如下：甲种方式用绳的长为4a+4b+8c，
乙种方式用绳的长为4a+6b+6c，丙种方式用绳的长为6a+6b+4c。
因为(4a+6b+6c)-(4a+4b+8c)=2b-2c＞0，所以乙＞甲；
因为(6a+6b+4c)-(4a+6b+6c)=2a-2c＞0，所以丙＞乙。
即丙＞乙＞甲。