第81页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
5. 如图,海上有两艘军舰$A$和$B$,由$A$测
得$B$的方向是(
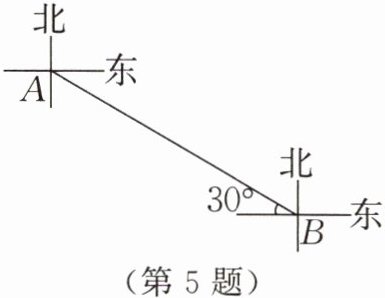
A.南偏东$30^{\circ}$
B.南偏东$60^{\circ}$
C.北偏西$30^{\circ}$
D.北偏西$60^{\circ}$
得$B$的方向是(
B
)。
A.南偏东$30^{\circ}$
B.南偏东$60^{\circ}$
C.北偏西$30^{\circ}$
D.北偏西$60^{\circ}$
答案:
5.B
6. 如图,$OC$是$\angle AOB$的平分线,$OD$是
$\angle BOC$的平分线,下列各式正确的是
(
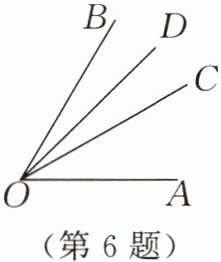
A.$\angle COD = \frac{1}{2}\angle AOB$
B.$\angle AOD = \frac{2}{3}\angle AOB$
C.$\angle BOD = \frac{1}{2}\angle AOD$
D.$\angle BOC = \frac{2}{3}\angle AOD$
$\angle BOC$的平分线,下列各式正确的是
(
D
)。
A.$\angle COD = \frac{1}{2}\angle AOB$
B.$\angle AOD = \frac{2}{3}\angle AOB$
C.$\angle BOD = \frac{1}{2}\angle AOD$
D.$\angle BOC = \frac{2}{3}\angle AOD$
答案:
6.D
7. 钟表显示$10$时$30$分时,时针与分针的夹角为
135°
。
答案:
7.135°
8. 如图,$AB$和$CD$都是直线,$\angle AOE =$
$90^{\circ}$,$\angle 3 = \angle FOD$,$\angle 1 = 27^{\circ}20'$,求$\angle 2$,
$\angle 3$的度数。
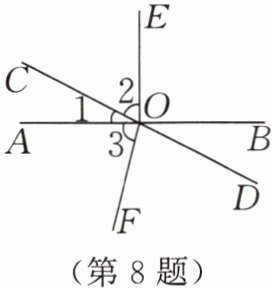
$90^{\circ}$,$\angle 3 = \angle FOD$,$\angle 1 = 27^{\circ}20'$,求$\angle 2$,
$\angle 3$的度数。

答案:
8.解:因为∠AOE = 90°,
所以∠2 = 90° - ∠1 = 90° - 27°20′ = 62°40′。
因为∠AOD = 180° - ∠1 = 180° - 27°20′ = 152°40′,∠3 = ∠FOD,
所以$∠3 = \frac{1}{2}∠AOD = 76°20′。$
所以∠2 = 90° - ∠1 = 90° - 27°20′ = 62°40′。
因为∠AOD = 180° - ∠1 = 180° - 27°20′ = 152°40′,∠3 = ∠FOD,
所以$∠3 = \frac{1}{2}∠AOD = 76°20′。$
9. 将一张多边形纸片沿一条直线剪下一个三角形后,变成一个六边形,则原多边形纸片的边数不可能是(
A.$5$
B.$6$
C.$7$
D.$8$
D
)。A.$5$
B.$6$
C.$7$
D.$8$
答案:
9.D
10. 如图,阴影部分扇形的圆心角是

36°
。
答案:
10.36°
11. 如图,在三角形广场$ABC$的三个角处
各建一个半径相等的扇形草坪,草坪的
半径为$20\ m$,求草坪的总面积。(结果
保留$\pi$)

各建一个半径相等的扇形草坪,草坪的
半径为$20\ m$,求草坪的总面积。(结果
保留$\pi$)

答案:
11.解:$S_{草坪} = \frac{180\pi×20^{2}}{360} = 200\pi(m^{2}),$
故草坪的总面积为$200\pi m^{2}。$
故草坪的总面积为$200\pi m^{2}。$
12. 观察下面的图形,并阅读图形下面的相
关文字:
四边形的对角线有$2$条,五边形的对角线有$5$条,六边形的对角线有$9$条。
通过分析上面的材料,请你说说十边形的对角线有多少条。你能总结出$n$边
形的对角线有多少条吗?

关文字:
四边形的对角线有$2$条,五边形的对角线有$5$条,六边形的对角线有$9$条。
通过分析上面的材料,请你说说十边形的对角线有多少条。你能总结出$n$边
形的对角线有多少条吗?

答案:
12.解:十边形的对角线有$\frac{10×(10 - 3)}{2} = 5×7 = 35($条),n边形的对角线有$\frac{n(n - 3)}{2}$条。
查看更多完整答案,请扫码查看


