第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1. (3分)在探究证明"三角形的内角和是$180^{\circ}$"时,综合实践小组的同学作了如下四种辅助线,其中不能证明"三角形的内角和是$180^{\circ}$"的是 (
[A]过点$C作EF// AB$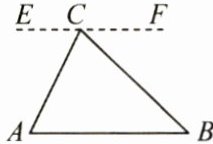
[B]过$AB上一点D分别作DE// BC$,$DF// AC$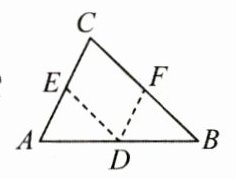
[C]延长$AC到点F$,过点$C作CE// AB$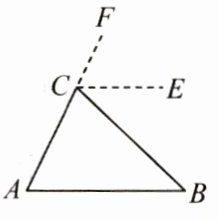
[D]作$CD\perp AB于点D$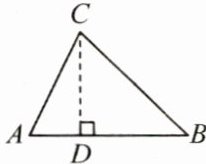
D
)[A]过点$C作EF// AB$

[B]过$AB上一点D分别作DE// BC$,$DF// AC$

[C]延长$AC到点F$,过点$C作CE// AB$

[D]作$CD\perp AB于点D$

答案:
D
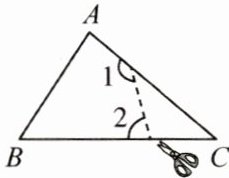
2. (3分)如图,在$\triangle ABC$中,$\angle C = 40^{\circ}$,按图中虚线将$\angle C$剪去后,$\angle 1+\angle 2$的度数和为 (
[A]$140^{\circ}$ [B]$210^{\circ}$ [C]$220^{\circ}$ [D]$320^{\circ}$
C
)[A]$140^{\circ}$ [B]$210^{\circ}$ [C]$220^{\circ}$ [D]$320^{\circ}$

答案:
C
3. (3分)如图,$AE$,$BD相交于点C$,$\angle A = 70^{\circ}$,$\angle B = 50^{\circ}$,则$\angle DCE$的度数为
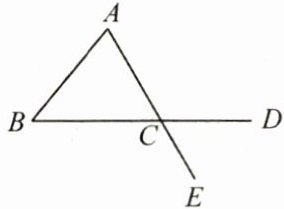
$60^{\circ}$
.
答案:
$60^{\circ}$
4. (3分)已知在$\triangle ABC$中,$\angle B = 2\angle A$,$\angle C = \angle A + 40^{\circ}$,则$\angle A$的度数为
$35^{\circ}$
.
答案:
$35^{\circ}$
5. (3分)已知在$Rt\triangle ABC$中,$\angle C$为直角,$\angle B是\angle A$的2倍,则$\angle A$的度数为 (
[A]$30^{\circ}$ [B]$50^{\circ}$ [C]$70^{\circ}$ [D]$90^{\circ}$
A
)[A]$30^{\circ}$ [B]$50^{\circ}$ [C]$70^{\circ}$ [D]$90^{\circ}$
答案:
A
6. (3分)下列条件:①$\angle A + \angle B = \angle C$;②$\angle A:\angle B:\angle C = 1:2:3$;③$\angle A = 90^{\circ} - \angle B$;④$\angle A = \angle B = \angle C$;⑤$\angle A = 2\angle B = 3\angle C$.其中能确定$\triangle ABC$是直角三角形的有 (
C
)
答案:
C 解析:①
∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形.②
∵∠A:∠B:∠C=1:2:3,
∴∠C=$\frac{3}{1+2+3}× 180^{\circ}$=90°,
∴△ABC是直角三角形.③
∵∠A=90°-∠B,
∴∠A+∠B=90°,
∴△ABC是直角三角形.④
∵∠A=∠B=∠C,∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°,
∴△ABC不是直角三角形.⑤
∵∠A=2∠B=3∠C,
∴设∠C=x,则∠A=3x,∠B=$\frac{3}{2}x$,
∵∠A+∠B+∠C=180°,
∴3x+$\frac{3}{2}x$+x=180°,解得x=$(\frac{360}{11})^{\circ}$,
∴∠A=$(\frac{1080}{11})^{\circ}$,∠B=$(\frac{540}{11})^{\circ}$,∠C=$(\frac{360}{11})^{\circ}$,
∴△ABC不是直角三角形.
∴能确定△ABC是直角三角形的条件有①②③,共有3个.故选C.
∵∠A+∠B=∠C,∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形.②
∵∠A:∠B:∠C=1:2:3,
∴∠C=$\frac{3}{1+2+3}× 180^{\circ}$=90°,
∴△ABC是直角三角形.③
∵∠A=90°-∠B,
∴∠A+∠B=90°,
∴△ABC是直角三角形.④
∵∠A=∠B=∠C,∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°,
∴△ABC不是直角三角形.⑤
∵∠A=2∠B=3∠C,
∴设∠C=x,则∠A=3x,∠B=$\frac{3}{2}x$,
∵∠A+∠B+∠C=180°,
∴3x+$\frac{3}{2}x$+x=180°,解得x=$(\frac{360}{11})^{\circ}$,
∴∠A=$(\frac{1080}{11})^{\circ}$,∠B=$(\frac{540}{11})^{\circ}$,∠C=$(\frac{360}{11})^{\circ}$,
∴△ABC不是直角三角形.
∴能确定△ABC是直角三角形的条件有①②③,共有3个.故选C.
7. (5分)如图,已知$DB$,$EC交于点A$,$\angle B = \angle E = 90^{\circ}$,$\angle C = 39^{\circ}$,求$\angle D$的度数.
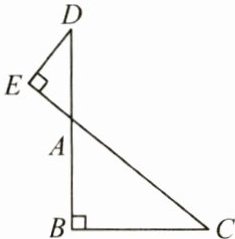

答案:
解:
∵∠B=∠E=90°,
∴∠C+∠BAC=∠D+∠DAE,
∵∠BAC=∠DAE(对顶角相等),
∴∠D=∠C=39°.
∵∠B=∠E=90°,
∴∠C+∠BAC=∠D+∠DAE,
∵∠BAC=∠DAE(对顶角相等),
∴∠D=∠C=39°.
查看更多完整答案,请扫码查看


