第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
10. (5 分)三角 表示 $ 3abc $, 方框
表示 $ 3abc $, 方框 表示 $ -4x^{y}w^{z} $, 求
表示 $ -4x^{y}w^{z} $, 求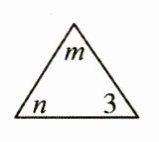
 .
.
 表示 $ 3abc $, 方框
表示 $ 3abc $, 方框 表示 $ -4x^{y}w^{z} $, 求
表示 $ -4x^{y}w^{z} $, 求
 .
.
答案:
解: =$9mn×(-4n^{2}m^{5})=-36m^{6}n^{3}.$
=$9mn×(-4n^{2}m^{5})=-36m^{6}n^{3}.$
解:
 =$9mn×(-4n^{2}m^{5})=-36m^{6}n^{3}.$
=$9mn×(-4n^{2}m^{5})=-36m^{6}n^{3}.$ 11. (6 分)先化简, 再求值: $ -10(-a^{3}b^{2}c)^{2} \cdot \frac{1}{5}a \cdot (bc)^{3} - (2abc)^{3} \cdot (-a^{2}b^{2}c)^{2} $, 其中 $ a = -5 $, $ b = 0.2 $, $ c = 2 $.
答案:
解:原式$=-2a^{7}b^{7}c^{5}-8a^{7}b^{7}c^{5}=-10a^{7}b^{7}c^{5},$
当$a=-5,b=0.2,c=2$时,
原式$=-10×(-5×0.2)^{7}×2^{5}=10×2^{5}=320.$
当$a=-5,b=0.2,c=2$时,
原式$=-10×(-5×0.2)^{7}×2^{5}=10×2^{5}=320.$
12. (4 分)有理数 $ x $, $ y $ 满足条件 $ |2x - 3y + 1| + (x + 3y + 5)^{2} = 0 $, 求代数式 $ (-2xy)^{2} \cdot (-y^{2}) \cdot 6xy^{2} $ 的值.
答案:
解:由题意,得$\left\{\begin{array}{l} 2x-3y+1=0,\\ x+3y+5=0,\end{array}\right. $
解得$\left\{\begin{array}{l} x=-2,\\ y=-1.\end{array}\right. $
$\therefore (-2xy)^{2}\cdot (-y^{2})\cdot 6xy^{2}$
$=4x^{2}y^{2}\cdot (-y^{2})\cdot 6xy^{2}$
$=-24x^{3}y^{6}.$
当$x=-2,y=-1$时,
原式$=-24×(-2)^{3}×(-1)^{6}=-24×(-8)=192.$
解得$\left\{\begin{array}{l} x=-2,\\ y=-1.\end{array}\right. $
$\therefore (-2xy)^{2}\cdot (-y^{2})\cdot 6xy^{2}$
$=4x^{2}y^{2}\cdot (-y^{2})\cdot 6xy^{2}$
$=-24x^{3}y^{6}.$
当$x=-2,y=-1$时,
原式$=-24×(-2)^{3}×(-1)^{6}=-24×(-8)=192.$
13. (6 分)计算:
(1) $ (-3a^{3})^{2} \cdot a^{3} + (-4a)^{2} \cdot a^{7} + (-5a^{3})^{3} $;
(2) $ (-x)^{2} \cdot x^{3} \cdot (-2y)^{3} + (-2xy)^{2} \cdot (-x)^{3}y $;
(3) $ (-\frac{1}{2}xy^{2})^{2} - 3xy^{3} \cdot (-2xy) $.
(1) $ (-3a^{3})^{2} \cdot a^{3} + (-4a)^{2} \cdot a^{7} + (-5a^{3})^{3} $;
(2) $ (-x)^{2} \cdot x^{3} \cdot (-2y)^{3} + (-2xy)^{2} \cdot (-x)^{3}y $;
(3) $ (-\frac{1}{2}xy^{2})^{2} - 3xy^{3} \cdot (-2xy) $.
答案:
解:
(1)原式$=9a^{6}\cdot a^{3}+16a^{2}\cdot a^{7}-125a^{9}=9a^{9}+16a^{9}-125a^{9}=-100a^{9}.$
(2)原式$=x^{2}\cdot x^{3}\cdot (-8y^{3})+4x^{2}y^{2}\cdot (-x^{3}y)=-8x^{5}y^{3}-4x^{5}y^{3}=-12x^{5}y^{3}.$
(3)原式$=\frac {1}{4}x^{2}y^{4}+6x^{2}y^{4}=\frac {25}{4}x^{2}y^{4}.$
(1)原式$=9a^{6}\cdot a^{3}+16a^{2}\cdot a^{7}-125a^{9}=9a^{9}+16a^{9}-125a^{9}=-100a^{9}.$
(2)原式$=x^{2}\cdot x^{3}\cdot (-8y^{3})+4x^{2}y^{2}\cdot (-x^{3}y)=-8x^{5}y^{3}-4x^{5}y^{3}=-12x^{5}y^{3}.$
(3)原式$=\frac {1}{4}x^{2}y^{4}+6x^{2}y^{4}=\frac {25}{4}x^{2}y^{4}.$
14. (6 分)已知 $ (2x^{3}y^{2}) \cdot (-3x^{m}y^{3}) \cdot (5x^{2}y^{n}) = -30x^{4}y^{2} $, 求 $ m + n $ 的值.
答案:
解:$(2x^{3}y^{2})\cdot (-3x^{m}y^{3})\cdot (5x^{2}y^{n})=-30x^{m+5}y^{n+5}=-30x^{4}y^{2},$
$\therefore m+5=4,n+5=2.$
$\therefore m=-1,n=-3.$
$\therefore m+n=-4.$
$\therefore m+5=4,n+5=2.$
$\therefore m=-1,n=-3.$
$\therefore m+n=-4.$
15. (10 分)已知 $ -2a^{2n}b $ 与 $ a^{3m + 1}b^{n + m - 1} $ 的积与单项式 $ 5(a^{3}b)^{2} × (a^{2}b) $ 是同类项. 求:
(1) $ (m - n)^{2025} $ 的值;
(2) $ -2a^{2n}b $ 与 $ a^{3m + 1}b^{n + m - 1} $ 的积.
(1) $ (m - n)^{2025} $ 的值;
(2) $ -2a^{2n}b $ 与 $ a^{3m + 1}b^{n + m - 1} $ 的积.
答案:
解:$\because -2a^{2n}b\cdot a^{3m+1}b^{n+m-1}=-2a^{3m+2n+1}b^{m+n}$与单项式$5(a^{3}b)^{2}×(a^{2}b)=5a^{8}b^{3}$是同类项,$\therefore 3m+2n+1=8,m+n=3,$
解得$m=1,n=2.$
(1)$(m-n)^{2025}=(1-2)^{2025}=-1.$
(2)$-2a^{2n}b\cdot a^{3m+1}b^{n+m-1}=-2a^{3m+2n+1}b^{m+n}=-2a^{3+4+1}b^{1+2}=-2a^{8}b^{3}.$
解得$m=1,n=2.$
(1)$(m-n)^{2025}=(1-2)^{2025}=-1.$
(2)$-2a^{2n}b\cdot a^{3m+1}b^{n+m-1}=-2a^{3m+2n+1}b^{m+n}=-2a^{3+4+1}b^{1+2}=-2a^{8}b^{3}.$
查看更多完整答案,请扫码查看


