《2025年同步练习册分层卷八年级数学上册人教版》

1. (3 分)在$\triangle ABC$中,$\angle A = 60^{\circ}$,$\angle B = 50^{\circ}$,$AB = 8$,下列条件能得到$\triangle ABC \cong \triangle DEF$的是(C)
[A] $\angle D = 60^{\circ}$,$\angle E = 50^{\circ}$,$DF = 8$
[B] $\angle D = 60^{\circ}$,$\angle F = 50^{\circ}$,$DE = 8$
[C] $\angle E = 50^{\circ}$,$\angle F = 70^{\circ}$,$DE = 8$
[D] $\angle D = 60^{\circ}$,$\angle F = 70^{\circ}$,$EF = 8$

答案： C

2. (3 分)王老师不小心将一块教学用的三角形玻璃打破了,他想再到玻璃店划一块同样大小的三角形玻璃,为了方便他只要带哪一块就可以(A)

[A] ① [B] ② [C] ③ [D] ④

答案： A

3. (3 分)如图,$\angle BAD = \angle CAE$,$AB = AD$,若添加一个条件可得$\triangle ABC \cong \triangle ADE$,对应的理由是 ASA,则添加的条件是∠B=∠ADE.

答案： ∠B=∠ADE

4. (6 分)如图,$AD是\triangle ABC$的中线,$E$,$F分别是AD和AD$延长线上的点,且$CE // BF$.$\triangle ECD与\triangle FBD$全等吗？请说明你的理由.

答案： 解：△ECD与△FBD全等.理由如下：
∵AD是△ABC的中线，
∴BD=CD.
∵CE//BF，
∴∠DCE=∠DBF.
在△ECD和△FBD中，
∠DCE=∠DBF，
CD=BD，
∠CDE=∠BDF，
∴△ECD≌△FBD(ASA).

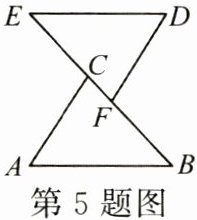
5. (3 分)如图,点$E$,$C$,$F$,$B$在一条直线上,$AB // ED$,$\angle A = \angle D$,添加下列条件不能判定$\triangle ABC \cong \triangle DEF$的是 (A)
[A] $AC // DF$ [B] $AB = DE$ [C] $EC = BF$ [D] $AC = DF$

答案： A

6. (3 分)如图,已知$P是\angle BAC的平分线AD$上的一点,请添加一个条件：∠B=∠C(答案不唯一),使得$\triangle ABP \cong \triangle ACP$.

答案： ∠B=∠C(答案不唯一)