第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
8. (3 分)如图,在 $ 4 × 4 $ 的正方形网格中,选择一个格子涂阴影,使得整个图形是以虚线为对称轴的轴对称图形,则涂阴影的格子应为(
[A] $ 4 $
[B] $ 3 $
[C] $ 2 $
[D] $ 1 $

D
)[A] $ 4 $
[B] $ 3 $
[C] $ 2 $
[D] $ 1 $

答案:
D
9. (3 分)如图,根据尺规作图的痕迹,$ \angle MBA $ 的度数为

40°
.
答案:
40°
10. (3 分)如图,$ \triangle ABC $ 的周长为 $ 15 \, cm $,根据图中尺规作图的痕迹,直线 $ DE $ 分别与 $ BC $,$ AC $ 交于 $ D $,$ E $ 两点. 若 $ AE = 2 \, cm $,则 $ \triangle ABD $ 的周长为______

11
$ cm $.
答案:
11 解析:由作图可知,DE 垂直平分线段 AC,
∴DA=DC,AE=EC.
∵AB+BC+AC=15 cm,AC=2AE=4 cm,
∴AB+BC=11 cm.
∴△ABD 的周长=AB+BD+DA=AB+BD+DC=AB+BC=11 cm.
∴DA=DC,AE=EC.
∵AB+BC+AC=15 cm,AC=2AE=4 cm,
∴AB+BC=11 cm.
∴△ABD 的周长=AB+BD+DA=AB+BD+DC=AB+BC=11 cm.
11. (14 分)如图,某城市公园里有三个景点 $ A $,$ B $,$ C $,直线 $ l_1 $,$ l_3 $ 表示直路,而 $ l_2 $ 表示弯路. 想在 $ S $ 区里修建一座公厕 $ P $,使它到两条路 $ l_1 $ 和 $ l_3 $ 的距离相等,且到两个景点 $ B $ 和 $ C $ 的距离也相等. 求点 $ P $ 的位置.(简述作图过程,说明理由)


答案:
解:如图,设 l₁和 l₃交于点 E,以点 E 为圆心,适当长为半径作弧,分别交 l₁,l₃于点 M,N.分别以点 M 和点 N 为圆心,大于$\frac{1}{2}$MN 的长为半径作弧,在 l₁,l₃的内部交于点 F,作射线 EF.连接 BC,分别以点 B 和点 C 为圆心,大于$\frac{1}{2}$BC 的长为半径作弧,两弧交于点 T,H,作直线 TH 与射线 EF 交于点 P,则点 P 为所求作的点. 理由如下:由作图可知 EF 为直线 l₁,l₃夹角的平分线,点 P 在 EF 上,
理由如下:由作图可知 EF 为直线 l₁,l₃夹角的平分线,点 P 在 EF 上,
∴点 P 到 l₁和 l₃的距离相等.由作图可知直线 TH 为线段 BC 的垂直平分线,点 P 在 TH 上,
∴PB=PC.
∴点 P 到 l₁和 l₃的距离相等,且到点 B 和点 C 的距离也相等.
解:如图,设 l₁和 l₃交于点 E,以点 E 为圆心,适当长为半径作弧,分别交 l₁,l₃于点 M,N.分别以点 M 和点 N 为圆心,大于$\frac{1}{2}$MN 的长为半径作弧,在 l₁,l₃的内部交于点 F,作射线 EF.连接 BC,分别以点 B 和点 C 为圆心,大于$\frac{1}{2}$BC 的长为半径作弧,两弧交于点 T,H,作直线 TH 与射线 EF 交于点 P,则点 P 为所求作的点.
 理由如下:由作图可知 EF 为直线 l₁,l₃夹角的平分线,点 P 在 EF 上,
理由如下:由作图可知 EF 为直线 l₁,l₃夹角的平分线,点 P 在 EF 上,∴点 P 到 l₁和 l₃的距离相等.由作图可知直线 TH 为线段 BC 的垂直平分线,点 P 在 TH 上,
∴PB=PC.
∴点 P 到 l₁和 l₃的距离相等,且到点 B 和点 C 的距离也相等.
12. (16 分)下面是某数学兴趣小组探究用不同方法作一条线段的垂直平分线的讨论片段,请仔细阅读,并完成相应任务.
小巩:如图(1),①分别以点 $ A $,$ B $ 为圆心,大于 $ \dfrac{1}{2}AB $ 的长为半径作弧,两弧交于点 $ P $;②分别作 $ \angle PAB $,$ \angle PBA $ 的平分线 $ AD $,$ BC $,交于点 $ E $;③作直线 $ PE $. 直线 $ PE $ 即为线段 $ AB $ 的垂直平分线.
简述作图理由:
由作图可知,$ PA = PB $,$ \therefore $ 点 $ P $ 在线段 $ AB $ 的垂直平分线上,$ \angle PAB = \angle PBA $.
$ \because AD $,$ BC $ 分别是 $ \angle PAB $,$ \angle PBA $ 的平分线,$ \therefore \angle DAB = \angle CBA $.
$ \therefore AE = BE $. $ \therefore $ 点 $ E $ 在线段 $ AB $ 的垂直平分线上.
$ \therefore $ 直线 $ PE $ 是线段 $ AB $ 的垂直平分线.
小义:我认为小巩的作图方法很有创意,但是可以改进如下,如图(2).
①分别以点 $ A $,$ B $ 为圆心,大于 $ \dfrac{1}{2}AB $ 的长为半径作弧,两弧交于点 $ P $;
②分别在线段 $ PA $,$ PB $ 上截取 $ PC = PD $;
③连接 $ AD $,$ BC $,交点为 $ E $;
④作直线 $ PE $.
直线 $ PE $ 即为线段 $ AB $ 的垂直平分线.
任务:
(1) 小巩得出点 $ P $ 在线段 $ AB $ 的垂直平分线上的依据是______.
(2) 小义作图得到的直线 $ PE $ 是线段 $ AB $的垂直平分线吗?请判断并说明理由.
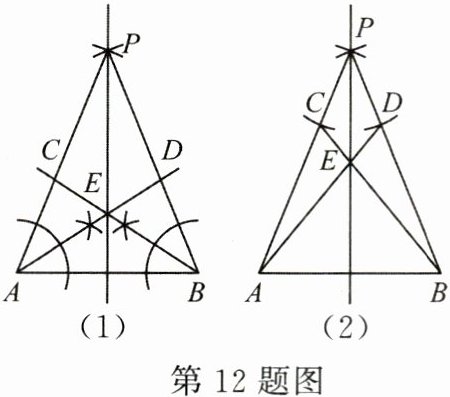
(1)
(2)直线 PE 是线段 AB 的垂直平分线.理由如下:由作图可知 PA=PB,PC=PD.在△APD 和△BPC 中,$\left\{\begin{array}{l} PA=PB,\\ ∠APD=∠BPC,\\ PD=PC,\end{array}\right.$
∴△APD≌△BPC(SAS).
∴∠PAD=∠PBC.
∵PA=PB,
∴点 P 在线段 AB 的垂直平分线上,∠PAB=∠PBA.
∴∠PAB - ∠PAD=∠PBA - ∠PBC,即∠DAB=∠CBA.
∴AE=BE.
∴点 E 在线段 AB 的垂直平分线上.
∴直线 PE 是线段 AB 的垂直平分线.
小巩:如图(1),①分别以点 $ A $,$ B $ 为圆心,大于 $ \dfrac{1}{2}AB $ 的长为半径作弧,两弧交于点 $ P $;②分别作 $ \angle PAB $,$ \angle PBA $ 的平分线 $ AD $,$ BC $,交于点 $ E $;③作直线 $ PE $. 直线 $ PE $ 即为线段 $ AB $ 的垂直平分线.
简述作图理由:
由作图可知,$ PA = PB $,$ \therefore $ 点 $ P $ 在线段 $ AB $ 的垂直平分线上,$ \angle PAB = \angle PBA $.
$ \because AD $,$ BC $ 分别是 $ \angle PAB $,$ \angle PBA $ 的平分线,$ \therefore \angle DAB = \angle CBA $.
$ \therefore AE = BE $. $ \therefore $ 点 $ E $ 在线段 $ AB $ 的垂直平分线上.
$ \therefore $ 直线 $ PE $ 是线段 $ AB $ 的垂直平分线.
小义:我认为小巩的作图方法很有创意,但是可以改进如下,如图(2).
①分别以点 $ A $,$ B $ 为圆心,大于 $ \dfrac{1}{2}AB $ 的长为半径作弧,两弧交于点 $ P $;
②分别在线段 $ PA $,$ PB $ 上截取 $ PC = PD $;
③连接 $ AD $,$ BC $,交点为 $ E $;
④作直线 $ PE $.
直线 $ PE $ 即为线段 $ AB $ 的垂直平分线.
任务:
(1) 小巩得出点 $ P $ 在线段 $ AB $ 的垂直平分线上的依据是______.
(2) 小义作图得到的直线 $ PE $ 是线段 $ AB $的垂直平分线吗?请判断并说明理由.

(1)
与线段两个端点距离相等的点在这条线段的垂直平分线上
(2)直线 PE 是线段 AB 的垂直平分线.理由如下:由作图可知 PA=PB,PC=PD.在△APD 和△BPC 中,$\left\{\begin{array}{l} PA=PB,\\ ∠APD=∠BPC,\\ PD=PC,\end{array}\right.$
∴△APD≌△BPC(SAS).
∴∠PAD=∠PBC.
∵PA=PB,
∴点 P 在线段 AB 的垂直平分线上,∠PAB=∠PBA.
∴∠PAB - ∠PAD=∠PBA - ∠PBC,即∠DAB=∠CBA.
∴AE=BE.
∴点 E 在线段 AB 的垂直平分线上.
∴直线 PE 是线段 AB 的垂直平分线.
答案:
(1) 与线段两个端点距离相等的点在这条线段的垂直平分线上
(2) 直线 PE 是线段 AB 的垂直平分线.理由如下:由作图可知 PA=PB,PC=PD.在△APD 和△BPC 中,$\left\{\begin{array}{l} PA=PB,\\ ∠APD=∠BPC,\\ PD=PC,\end{array}\right. $
∴△APD≌△BPC(SAS).
∴∠PAD=∠PBC.
∵PA=PB,
∴点 P 在线段 AB 的垂直平分线上,∠PAB=∠PBA.
∴∠PAB - ∠PAD=∠PBA - ∠PBC,即∠DAB=∠CBA.
∴AE=BE.
∴点 E 在线段 AB 的垂直平分线上.
∴直线 PE 是线段 AB 的垂直平分线.
(1) 与线段两个端点距离相等的点在这条线段的垂直平分线上
(2) 直线 PE 是线段 AB 的垂直平分线.理由如下:由作图可知 PA=PB,PC=PD.在△APD 和△BPC 中,$\left\{\begin{array}{l} PA=PB,\\ ∠APD=∠BPC,\\ PD=PC,\end{array}\right. $
∴△APD≌△BPC(SAS).
∴∠PAD=∠PBC.
∵PA=PB,
∴点 P 在线段 AB 的垂直平分线上,∠PAB=∠PBA.
∴∠PAB - ∠PAD=∠PBA - ∠PBC,即∠DAB=∠CBA.
∴AE=BE.
∴点 E 在线段 AB 的垂直平分线上.
∴直线 PE 是线段 AB 的垂直平分线.
查看更多完整答案,请扫码查看


