《2025年同步练习册分层卷八年级数学上册人教版》

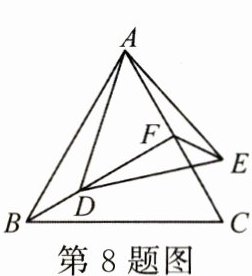
8. (3 分) 如图, 在等边三角形 $ ABC $ 中, $ BF $ 是边 $ AC $ 上的中线, 点 $ D $ 在 $ BF $ 上, 连接 $ AD $, 在 $ AD $ 的右侧作等边三角形 $ ADE $, 连接 $ EF $, 当 $ △AEF $ 的周长最小时, $ ∠FAE $ 的度数是 ( )
[A] $ 30^{\circ} $ [B] $ 45^{\circ} $ [C] $ 60^{\circ} $ [D] $ 90^{\circ} $

答案：
A 解析：如图，连接 CE.

由题意知 AB=AC，AD=AE，∠BAC=∠DAE=∠ABC=60°，
∴∠BAD=∠CAE.
∴△BAD≌△CAE(SAS).
∴∠ABD=∠ACE.
∵BF 是边 AC 上的中线，
∴AF=CF，∠ABD=∠CBD=∠ACE=30°.
∴点 E 在射线 CE 上运动(∠ACE=30°).
作点 A 关于直线 CE 的对称点 M，连接 FM 交 CE 于点 E'，此时 AE'+FE'的值最小，此时△AEF 的周长=AE+EF+AF=AE'+FE'+AF.
∵CA=CM，∠ACM=2∠ACE=60°，
∴△ACM 为等边三角形.
∵AF=CF，
∴FM⊥AC.
∴MF 垂直平分 AC.
∴AE'=CE'.
∴∠FAE'=∠ACE'=30°.

9. (3 分) 如图, 等边三角形 $ ABC $ 的边长为 3, $ A, B, A_1 $ 三点在一条直线上, 且 $ △ABC ≌ △A_1BC_1 $. 若 $ D $ 为线段 $ BC_1 $ 上一动点, 则 $ AD + CD $ 的最小值是 .

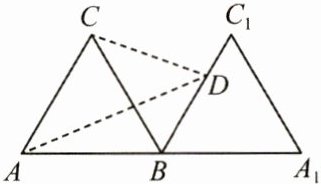
答案：
6 解析：如图，连接 CA₁交 BC₁于点 E，过点 B 作直线 l⊥AB.

∵△ABC 是等边三角形，△ABC≌△A₁BC₁，
∴△A₁BC₁是等边三角形，A₁B=AB=3.
∵A，B，A₁三点在一条直线上，
∴△ABC 与△A₁BC₁关于直线 l 对称.
∵∠ABC=∠A₁BC₁=60°.
∴∠CBC₁=60°.
∴∠C₁BA₁=∠C₁BC.
∵BA₁=BC，
∴BD⊥CA₁，CD=DA₁.
∴点 C，A₁关于直线 BC₁对称.
∴当点 D 与 B 重合时，AD+CD 的值最小，最小值等于线段 AA₁的长，为 6.

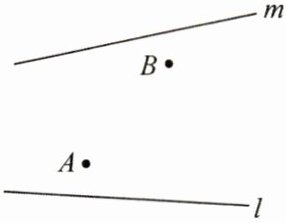
10. (11 分) 如图, 在旷野上, 一个人骑着马从 $ A $ 到 $ B $, 半路上他必须先到河岸 $ l $ 的点 $ P $ 处让马饮水, 然后再让马到河岸 $ m $ 的点 $ Q $ 处再次饮水, 最后到达点 $ B $, 他应该如何选择饮马地点 $ P, Q $, 才能使所走路程 $ AP + PQ + QB $ 最短? (假设河岸 $ l, m $ 为直线)

答案：
解：如图，分别作点 A 关于直线 l 的对称点 A'，点 B 关于直线 m 的对称点 B'，连接 A'B'，分别交 l 于点 P，交 m 于点 Q，连接 AP，BQ，此时路程 AP+PQ+BQ 最短.

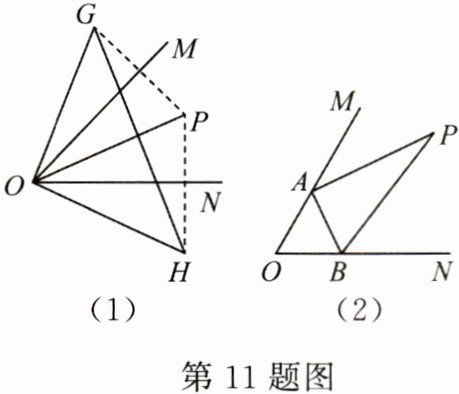
11. (17 分) 已知点 $ P $ 在 $ ∠MON $ 内.
(1) 如图 (1), 点 $ P $ 关于射线 $ OM $ 的对称点是点 $ G $, 点 $ P $ 关于射线 $ ON $ 的对称点是点 $ H $, 连接 $ OG, OH, OP $.
① 若 $ ∠MON = 50^{\circ} $, 则 $ ∠GOH = $ ; (填度数)
② 若 $ PO = 5 $, 连接 $ GH $, 请说明当 $ ∠MON $ 为多少度时, $ GH = 10 $.
(2) 如图 (2), 若 $ ∠MON = 60^{\circ} $, $ A, B $ 分别是射线 $ OM, ON $ 上的任意一点, 当 $ △PAB $ 的周长最小时, 求 $ ∠APB $ 的度数.

答案：
解：
(1)①100°
②
∵PO=5，
∴GO=HO=5.
当∠MON=90°时，∠GOH=180°，
∴点 G，O，H 在同一条直线上，
∴GH=GO+HO=10.
(2)如图，分别作点 P 关于 OM，ON 的对称点 P'，P''，连接 OP'，OP''，P'P''，P'P''分别交 OM，ON 于点 A，B，连接 PA，PB，则 AP=AP'，BP=BP''，此时△PAB 周长的最小值等于 P'P''的长.
由轴对称的性质，得 OP'=OP''=OP，∠P'OA=∠POA，∠P''OB=∠POB，
∴∠P'OP''=2∠MON=2×60°=120°.
∴∠OP'P''=∠OP''P'=(180°-120°)÷2=30°.
∴∠OPA=∠OP'A=30°.
同理可得∠OPB=∠OP''B=30°，
∴∠APB=30°+30°=60°.