《2025年同步练习册分层卷八年级数学上册人教版》

8. (9 分)如图,已知 $ \angle A = 75^{\circ} $,$ \angle B = 25^{\circ} $,$ \angle C = 35^{\circ} $,求 $ \angle BDC $ 和 $ \angle 1 $ 的度数。

答案： 解:
∵∠A = 75°,∠C = 35°,
∴∠BDC = ∠A + ∠C = 75° + 35° = 110°.
∵∠B = 25°,
∴∠1 = ∠BDC + ∠B = 110° + 25° = 135°.

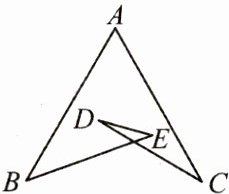
9. (3 分)如图,已知 $ \angle A = 60^{\circ} $,$ \angle B = 40^{\circ} $,$ \angle C = 30^{\circ} $,则 $ \angle D + \angle E $ 等于(C)

[A] $ 30^{\circ} $
[B] $ 40^{\circ} $
[C] $ 50^{\circ} $
[D] $ 60^{\circ} $

答案： C

10. (3 分)某工人加工一个机器零件(数据如图),经过测量这个零件不符合标准。标准要求是：$ \angle EFD = 120^{\circ} $,且 $ \angle A $,$ \angle B $,$ \angle E $ 保持不变。为了达到标准,工人在保持 $ \angle E $ 不变的情况下,应将图中 $ \angle D $ ______(填“增大”或“减小”) ______$ ^{\circ} $,横线处应分别填( )

[A] 减小；15
[B] 增大；15
[C] 减小；5
[D] 增大；5

答案：
A 解析:如图，延长 EF 交 CD 于点 H.

∵∠B = 50°,∠A = 70°,
∴∠DCE = ∠ACB = 180° - ∠A - ∠B = 60°.
∴∠DHE = ∠E + ∠DCE = 100°.
∵∠DFE = ∠D + ∠DHF,
∴∠D = ∠DFE - ∠DHF = 120° - 100° = 20°.
∴∠D 从 35°减小到 20°,减小了 15°.
故选 A.

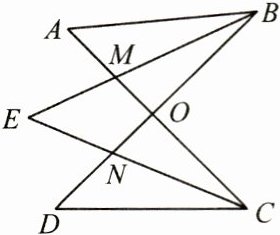
11. (12 分)如图,$ AC $,$ BD $ 相交于点 $ O $,$ BE $,$ CE $ 分别平分 $ \angle ABD $,$ \angle ACD $,$ \angle A = 50^{\circ} $,$ \angle D = 44^{\circ} $,求 $ \angle E $ 的度数。

答案： 解:
∵∠BNC = ∠D + ∠DCN,∠BNC = ∠E + ∠EBN,
∴∠D + ∠DCN = ∠E + ∠EBN.
同理,∠A + ∠ABE = ∠E + ∠ACE,
∴∠D + ∠DCN + ∠A + ∠ABE = 2∠E + ∠EBN + ∠ACE.
∵BE,CE 分别平分∠ABD,∠ACD,
∴∠DCN = ∠ACE,∠ABE = ∠EBN.
∴∠D + ∠A = 2∠E.
∵∠A = 50°,∠D = 44°,
∴∠E = 47°.

12. (12 分)用几何画板工具可以很方便地画出正五角星,如图(1)所示。
(1)在图(1)中,$ \angle A + \angle B + \angle C + \angle D + \angle E = $_________$ $；(填度数)
(2)拖动点 $ A $ 分别到图(2)和图(3)的位置时,$ \angle CAD + \angle B + \angle C + \angle D + \angle E $ 的值是否发生变化？说明你的理由。

答案：
解:
(1)如图
(1),设 BD，CE 交于点 M,AD,CE 交于点 N,则∠A + ∠C = ∠MND,∠B + ∠E = ∠DMN.
又
∵∠MND + ∠DMN + ∠D = 180°,
∴∠A + ∠B + ∠C + ∠D + ∠E = 180°.
故答案为 180°.
(2)∠CAD + ∠B + ∠C + ∠D + ∠E 的值没有变化.理由如下:
如图
(2)、图
(3)，设 BD,CE 交于点 M,AD,CE 交于点 N,则∠CAD + ∠C = ∠MND,∠B + ∠E = ∠DMN.
又
∵∠MND + ∠DMN + ∠D = 180°,
∴∠CAD + ∠B + ∠C + ∠D + ∠E = 180°.