第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1.(3分)在$\triangle ABC$中,已知$\angle B = \angle C$,则 (
[A]$AB = BC$ [B]$AB = AC$
[C]$BC = AC$ [D]$\angle A = 60^{\circ}$
B
)[A]$AB = BC$ [B]$AB = AC$
[C]$BC = AC$ [D]$\angle A = 60^{\circ}$
答案:
B
2.(3分)对“等角对等边”这句话的理解,正确的是 (
[A]只要两个角相等,那么它们所对的边也相等
[B]在两个三角形中,如果有两个角相等,那么它们所对的边也相等
[C]在一个三角形中,如果有两个角相等,那么它们所对的边也相等
[D]以上说法都是正确的
C
)[A]只要两个角相等,那么它们所对的边也相等
[B]在两个三角形中,如果有两个角相等,那么它们所对的边也相等
[C]在一个三角形中,如果有两个角相等,那么它们所对的边也相等
[D]以上说法都是正确的
答案:
C
3.(3分)如图,$\angle A = 36^{\circ}$,$\angle DBC = 36^{\circ}$,$\angle C = 72^{\circ}$,则图中等腰三角形有(
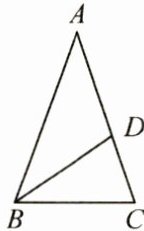
[A]0个 [B]1个 [C]2个 [D]3个
D
) 
[A]0个 [B]1个 [C]2个 [D]3个
答案:
D
4.(3分)根据下列图形提供的角度,不能用一条直线把一个三角形分成两个等腰三角形的是 (
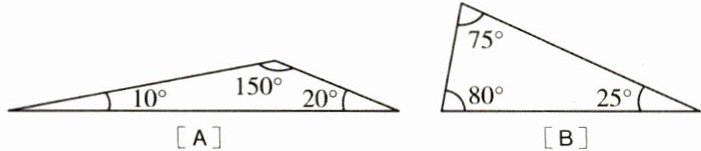
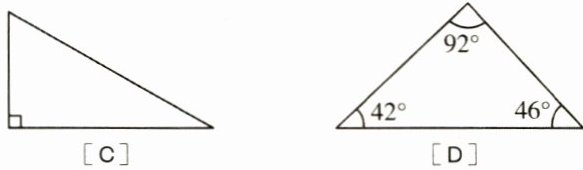
D
)

答案:
D
5.(3分)如图,$\angle BAC = 100^{\circ}$,$\angle B = 40^{\circ}$,$\angle D = 20^{\circ}$,$AB = 3$,则$CD = \underline{\hspace{2cm}}$.
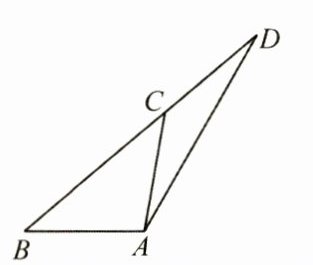

3
答案:
3
6.(5分)如图,$AD = BC$,$AC = BD$,求证:$\triangle EAB$是等腰三角形.
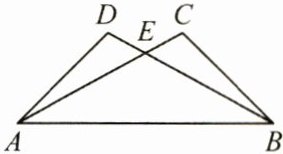

答案:
证明:在△ADB 和△BCA 中,AD=BC,BD=AC,AB=BA,
∴△ADB≌△BCA(SSS).
∴∠DBA=∠CAB.
∴AE=BE.
∴△EAB 是等腰三角形.
∴△ADB≌△BCA(SSS).
∴∠DBA=∠CAB.
∴AE=BE.
∴△EAB 是等腰三角形.
7.(8分)(2024·陕西)如图,已知直线$l和l外一点A$,请用尺规作图法,求作一个等腰直角三角形$ABC$,使得顶点$B和顶点C都在直线l$上.(作出符合题意的一个等腰直角三角形即可,保留作图痕迹,不写作法)


答案:
解:如图,等腰直角三角形 ABC 即为所求.
解:如图,等腰直角三角形 ABC 即为所求.

查看更多完整答案,请扫码查看


