第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
1. (3 分) 如图, 直线 $ l $ 是一条河, $ P, Q $ 是两个村庄, 欲在 $ l $ 上的某处修建一个水泵站, 向 $ P, Q $ 两地供水, 现有如下四种铺设方案, 图中实线表示铺设的管道, 则所需管道最短的是 (
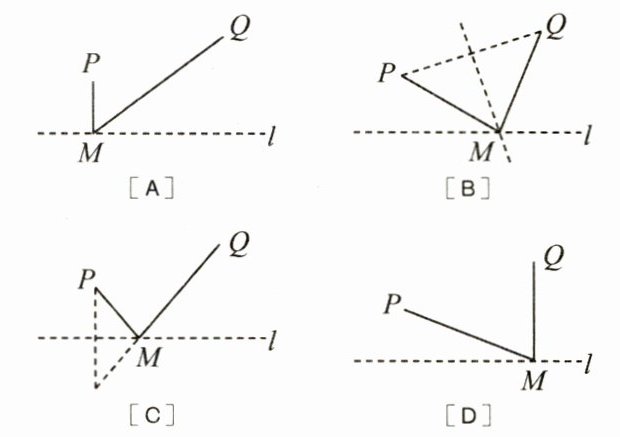
C
)
答案:
C
2. (3 分) 如图, 在等边三角形 $ ABC $ 中, 点 $ D, E $ 分别是 $ BC, AC $ 的中点, 点 $ P $ 是 $ AD $ 上的一个动点, 当 $ PC + PE $ 最小时, $ ∠CPE $ 的度数为 (
[A] $ 22.5^{\circ} $ [B] $ 30^{\circ} $ [C] $ 45^{\circ} $ [D] $ 60^{\circ} $

D
)[A] $ 22.5^{\circ} $ [B] $ 30^{\circ} $ [C] $ 45^{\circ} $ [D] $ 60^{\circ} $

答案:
D
3. (3 分) 如图, 高速公路的同一侧有 $ A, B $ 两城镇, 它们到高速公路所在直线 $ MN $ 的距离分别为 $ AC = 2 km, BD = 4 km, CD = 8 km $. 要在高速公路上 $ C, D $ 之间建一个出口 $ P $, 使 $ A, B $ 两城镇到 $ P $ 的距离之和最小, 则这个最短距离为
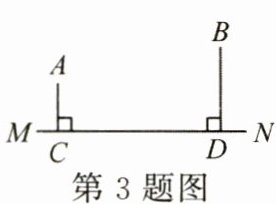
10 km
.
答案:
10 km
4. (3 分) 如图, 在 $ Rt△ABC $ 中, $ ∠C = 90^{\circ}, ∠B = 30^{\circ}, BC = 6 $, $ D $ 为 $ AB $ 的中点, $ P $ 为 $ BC $ 上一动点, 连接 $ AP, DP $, 则 $ AP + DP $ 的最小值是
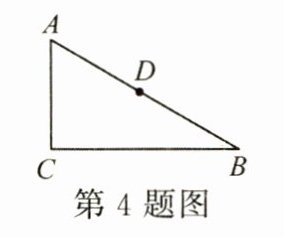
6
. 
答案:
6
5. (3 分) 如图, 在正方形 $ ABCD $ 中, 点 $ E $ 是 $ BC $ 上的一定点, 且 $ BE = 10, EC = 14 $, 点 $ P $ 是 $ BD $ 上的一动点, 则 $ PE + PC $ 的最小值是
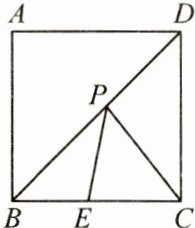
26
.
答案:
26
6. (8 分) 如图, 点 $ P $ 是四边形 $ ABCD $ 内一点, 分别在边 $ AB, BC $ 上作出点 $ M $, 点 $ N $, 使 $ PM + PN + MN $ 的值最小, 保留作图痕迹, 不写作法.
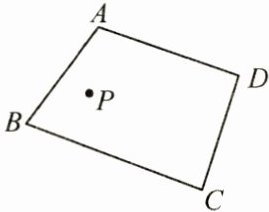

答案:
解:如图所示.

解:如图所示.

7. (3 分) 如图, 在 $ △ABC $ 中, $ AB = 5 $, $ BC = 10 $, $ AC = 9 $, $ MN $ 为边 $ BC $ 的垂直平分线, 点 $ D $ 为直线 $ MN $ 上一动点, 则 $ △ABD $ 的周长的最小值为 ( )
[A] 10 [B] 12 [C] 14 [D] 15
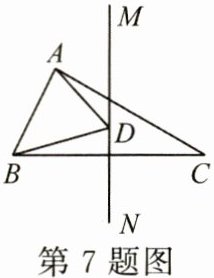
[A] 10 [B] 12 [C] 14 [D] 15

答案:
C 解析:如图,连接 DC.

∵AD,CD,AC 是△ACD 的三条边,
∴AD+DC≥AC.
∵MN 为边 BC 的垂直平分线,
∴DC=BD.
∴△ABD 的周长=AB+AD+DB=AB+AD+DC≥AB+AC=5+9=14.
C 解析:如图,连接 DC.

∵AD,CD,AC 是△ACD 的三条边,
∴AD+DC≥AC.
∵MN 为边 BC 的垂直平分线,
∴DC=BD.
∴△ABD 的周长=AB+AD+DB=AB+AD+DC≥AB+AC=5+9=14.
查看更多完整答案,请扫码查看


