《2025年暑假生活北京师范大学出版社高二数学人教版》

【典例 1】如图 3 - 2,在四棱锥 $ P - ABCD $ 中,$ PA \perp $ 平面 $ ABCD $,$ AD \perp CD $,$ AD // BC $,$ PA = AD = CD = 2 $,$ BC = 3 $。$ E $ 为 $ PD $ 的中点,点 $ F $ 在 $ PC $ 上,且 $ \frac{PF}{PC} = \frac{1}{3} $。

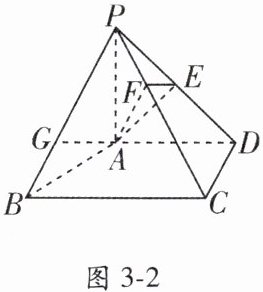
(1) 求证：$ CD \perp $ 平面 $ PAD $；
(2) 求二面角 $ F - AE - P $ 的余弦值；
(3) 设点 $ G $ 在 $ PB $ 上,且 $ \frac{PG}{PB} = \frac{2}{3} $,判断直线 $ AG $ 是否在平面 $ AEF $ 内,并说明理由。

答案：

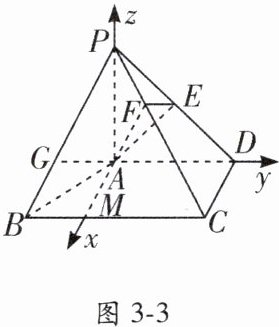
(1) 证明：因为 $ PA \perp $ 平面 $ ABCD $,所以 $ PA \perp CD $。

又因为 $ AD \perp CD $,$ PA \cap AD = A $,所以 $ CD \perp $ 平面 $ PAD $。

(2) 解：过点 $ A $ 作 $ AD $ 的垂线交 $ BC $ 于点 $ M $。因为 $ PA \perp $ 平面 $ ABCD $,所以 $ PA \perp AM $,$ PA \perp AD $。建立如图 3 - 3 所示的空间直角坐标系 $ Axyz $,则 $ A(0, 0, 0) $,$ B(2, - 1, 0) $,$ C(2, 2, 0) $,$ D(0, 2, 0) $,$ P(0, 0, 2) $。因为 $ E $ 为 $ PD $ 的中点,所以 $ E(0, 1, 1) $,所以 $ \overrightarrow{AE} = (0, 1, 1) $,$ \overrightarrow{PC} = (2, 2, - 2) $,$ \overrightarrow{AP} = (0, 0, 2) $。所以 $ \overrightarrow{PF} = \frac{1}{3} \overrightarrow{PC} = \left( \frac{2}{3}, \frac{2}{3}, - \frac{2}{3} \right) $,所以 $ \overrightarrow{AF} = \overrightarrow{AP} + \overrightarrow{PF} = \left( \frac{2}{3}, \frac{2}{3}, \frac{4}{3} \right) $。

设平面 $ AEF $ 的法向量为 $ \boldsymbol{n} = (x, y, z) $,则 $ \begin{cases} \boldsymbol{n} \cdot \overrightarrow{AE} = 0 \\ \boldsymbol{n} \cdot \overrightarrow{AF} = 0 \end{cases} $,即 $ \begin{cases} y + z = 0 \\ \frac{2}{3}x + \frac{2}{3}y + \frac{4}{3}z = 0 \end{cases} $。

令 $ z = 1 $,则 $ y = - 1 $,$ x = - 1 $。于是 $ \boldsymbol{n} = (- 1, - 1, 1) $。又因为平面 $ PAD $ 的一个法向量为 $ \boldsymbol{p} = (1, 0, 0) $,所以 $ \cos \langle \boldsymbol{n}, \boldsymbol{p} \rangle = \frac{\boldsymbol{n} \cdot \boldsymbol{p}}{|\boldsymbol{n}| |\boldsymbol{p}|} = - \frac{\sqrt{3}}{3} $。由题知,二面角 $ F - AE - P $ 为锐角,所以其余弦值为 $ \frac{\sqrt{3}}{3} $。

(3) 解：直线 $ AG $ 在平面 $ AEF $ 内。理由如下：

因为点 $ G $ 在 $ PB $ 上,且 $ \frac{PG}{PB} = \frac{2}{3} $,在
(2) 中的坐标系下,$ \overrightarrow{PB} = (2, - 1, - 2) $,所以 $ \overrightarrow{PG} = \frac{2}{3} \overrightarrow{PB} = \left( \frac{4}{3}, - \frac{2}{3}, - \frac{4}{3} \right) $,所以 $ \overrightarrow{AG} = \overrightarrow{AP} + \overrightarrow{PG} = \left( \frac{4}{3}, - \frac{2}{3}, \frac{2}{3} \right) $。由
(2) 知,平面 $ AEF $ 的一个法向量为 $ \boldsymbol{n} = (- 1, - 1, 1) $,所以 $ \overrightarrow{AG} \cdot \boldsymbol{n} = - \frac{4}{3} + \frac{2}{3} + \frac{2}{3} = 0 $。所以直线 $ AG $ 在平面 $ AEF $ 内。