2025年暑假生活北京师范大学出版社高二数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活北京师范大学出版社高二数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
4. 已知$A,B,C$三点不共线, 对平面$ABC外的任意一点O$, 下列条件中能确定点$M与点A,B,C$共面的是(
A.$\overrightarrow{OM}= \frac{1}{2}\overrightarrow{OA}-\overrightarrow{OB}+\overrightarrow{OC}$
B.$\overrightarrow{OM}= \overrightarrow{OA}-\frac{1}{2}\overrightarrow{OB}-\overrightarrow{OC}$
C.$\overrightarrow{OM}= \frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\overrightarrow{OC}$
D.$\overrightarrow{OM}= \frac{1}{2}\overrightarrow{OA}-\frac{1}{2}\overrightarrow{OB}+\overrightarrow{OC}$
D
).A.$\overrightarrow{OM}= \frac{1}{2}\overrightarrow{OA}-\overrightarrow{OB}+\overrightarrow{OC}$
B.$\overrightarrow{OM}= \overrightarrow{OA}-\frac{1}{2}\overrightarrow{OB}-\overrightarrow{OC}$
C.$\overrightarrow{OM}= \frac{1}{2}\overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\overrightarrow{OC}$
D.$\overrightarrow{OM}= \frac{1}{2}\overrightarrow{OA}-\frac{1}{2}\overrightarrow{OB}+\overrightarrow{OC}$
答案:
4.D 解析:若M,A,B,C四点共面,则$\overrightarrow {OM}=a\overrightarrow {OA}+b\overrightarrow {OB}+c\overrightarrow {OC}(a+b+c=1)$,在选项中只有D符合.故选D.
5. 如图1-6, 已知平行四边形$ABCD$中, $AD = 4,CD = 3,\angle D = 60^{\circ},PA\perp平面ABCD$, 且$PA = 6$, 则$PC$等于(
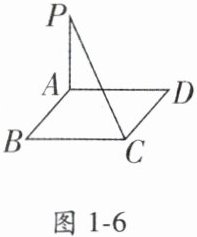
A.$3$
B.$7$
C.$4$
D.$6$
B
).
A.$3$
B.$7$
C.$4$
D.$6$
答案:
5.B 解析:$|\overrightarrow {PC}|^{2}=(\overrightarrow {PA}+\overrightarrow {AD}+\overrightarrow {DC})^{2}=|\overrightarrow {PA}|^{2}+|\overrightarrow {AD}|^{2}+|\overrightarrow {DC}|^{2}+2\overrightarrow {PA}\cdot \overrightarrow {AD}+2\overrightarrow {AD}\cdot \overrightarrow {DC}+2\overrightarrow {PA}\cdot \overrightarrow {DC}=6^{2}+4^{2}+3^{2}+2|\overrightarrow {AD}||\overrightarrow {DC}|\cos 120^{\circ }=49$.所以$|\overrightarrow {PC}|=7$.故选B.
6. 已知$a,b$是异面直线, $A,B\in a,C,D\in b,AC\perp b,BD\perp b$, 且$AB = 2,CD = 1$, 则$a与b$所成的角是(
A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$90^{\circ}$
C
).A.$30^{\circ}$
B.$45^{\circ}$
C.$60^{\circ}$
D.$90^{\circ}$
答案:
6.C 解析:$\overrightarrow {AB}=\overrightarrow {AC}+\overrightarrow {CD}+\overrightarrow {DB}$,所以$\overrightarrow {AB}\cdot \overrightarrow {CD}=(\overrightarrow {AC}+\overrightarrow {CD}+\overrightarrow {DB})\cdot \overrightarrow {CD}=\overrightarrow {AC}\cdot \overrightarrow {CD}+\overrightarrow {CD}^{2}+\overrightarrow {DB}\cdot \overrightarrow {CD}=0+1^{2}+0=1$.又$|\overrightarrow {AB}|=2,|\overrightarrow {CD}|=1$,所以$\cos \langle \overrightarrow {AB},\overrightarrow {CD}\rangle =\frac {\overrightarrow {AB}\cdot \overrightarrow {CD}}{|\overrightarrow {AB}||\overrightarrow {CD}|}=\frac {1}{2× 1}=\frac {1}{2}$.因为异面直线所成的角是锐角或直角,所以a与b所成的角是$60^{\circ }$.
7. (多选)已知$A,B,C$三点不共线, $O为平面ABC$外任一点, 则“点$M与点A,B,C$共面”的充分条件是(
A.$\overrightarrow{OM}= 2\overrightarrow{OA}-\overrightarrow{OB}-\overrightarrow{OC}$
B.$\overrightarrow{OM}= \overrightarrow{OA}+\overrightarrow{OB}-\overrightarrow{OC}$
C.$\overrightarrow{OM}= \overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$
D.$\overrightarrow{OM}= \frac{1}{2}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{6}\overrightarrow{OC}$
BD
).A.$\overrightarrow{OM}= 2\overrightarrow{OA}-\overrightarrow{OB}-\overrightarrow{OC}$
B.$\overrightarrow{OM}= \overrightarrow{OA}+\overrightarrow{OB}-\overrightarrow{OC}$
C.$\overrightarrow{OM}= \overrightarrow{OA}+\frac{1}{2}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$
D.$\overrightarrow{OM}= \frac{1}{2}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{6}\overrightarrow{OC}$
答案:
7.BD 解析:根据“$\overrightarrow {OM}=x\overrightarrow {OA}+y\overrightarrow {OB}+z\overrightarrow {OC}$,若$x+y+z=1$,则点M与点A,B,C共面”,分别判断各选项是不是充分条件.因为$2+(-1)+(-1)=0≠1,1+1+(-1)=1,1+\frac {1}{2}+\frac {1}{3}=\frac {11}{6}≠1,\frac {1}{2}+\frac {1}{3}+\frac {1}{6}=1$,所以B,D满足要求.故选BD.
8. 已知$A,B,C$三点共线, 则对空间任一点$O$, 存在三个不为零的实数$\lambda,m,n$, 使$\lambda\overrightarrow{OA}+m\overrightarrow{OB}+n\overrightarrow{OC}= \boldsymbol{0}$, 那么$\lambda + m + n$的值为______
0
.
答案:
8.0 解析:因为A,B,C三点共线,所以存在唯一实数k,使$\overrightarrow {AB}=k\overrightarrow {AC}$,即$\overrightarrow {OB}-\overrightarrow {OA}=k(\overrightarrow {OC}-\overrightarrow {OA})$,所以$(k - 1)\overrightarrow {OA}+\overrightarrow {OB}-k\overrightarrow {OC}=0$.又$\lambda \overrightarrow {OA}+m\overrightarrow {OB}+n\overrightarrow {OC}=0$,所以$\lambda = k - 1,m = 1,n = -k$,则$\lambda + m + n = 0$.
9. 正四面体$ABCD的棱长为2$, 半径为$\sqrt{2}的球O过点D$, $MN为球O$的一条直径, 则$\overrightarrow{AM}\cdot\overrightarrow{AN}$的最小值是______
$4 - 4\sqrt {2}$
.
答案:
9.$4 - 4\sqrt {2}$ 解析:由题意可知$OD = OM = ON$,则$\triangle MDN$是以点D为直角顶点的直角三角形,所以$\overrightarrow {AM}\cdot \overrightarrow {AN}=(\overrightarrow {AD}+\overrightarrow {DM})\cdot (\overrightarrow {AD}+\overrightarrow {DN})=\overrightarrow {AD}^{2}+\overrightarrow {AD}\cdot (\overrightarrow {DM}+\overrightarrow {DN})+\overrightarrow {DM}\cdot \overrightarrow {DN}=4+2\overrightarrow {AD}\cdot \overrightarrow {DO}+0$,当向量$\overrightarrow {AD},\overrightarrow {DO}$反向时,$\overrightarrow {AM}\cdot \overrightarrow {AN}$取得最小值,最小值为$4 - 2×2×\sqrt {2}=4 - 4\sqrt {2}$.
10. 如图1-7, 已知四边形$ABCD,ABEF$都是平行四边形且不共面, $M,N分别是AC,BF$的中点, 判断$\overrightarrow{CE}与\overrightarrow{MN}$是否共线.
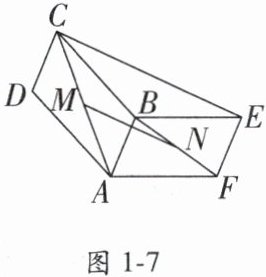

答案:
10.解:因为M,N分别是AC,BF的中点,且四边形ABCD,ABEF都是平行四边形,所以$\overrightarrow {MN}=\overrightarrow {MA}+\overrightarrow {AF}+\overrightarrow {FN}=\frac {1}{2}\overrightarrow {CA}+\overrightarrow {AF}+\frac {1}{2}\overrightarrow {FB}$.又$\overrightarrow {MN}=\overrightarrow {MC}+\overrightarrow {CE}+\overrightarrow {EB}+\overrightarrow {BN}=-\frac {1}{2}\overrightarrow {CA}+\overrightarrow {CE}-\overrightarrow {AF}-\frac {1}{2}\overrightarrow {FB}$,以上两式相加,得$\overrightarrow {CE}=2\overrightarrow {MN}$,即$\overrightarrow {CE}$与$\overrightarrow {MN}$共线.
11. 如图1-8, 已知线段$AB在平面\alpha$内, 线段$AC\perp\alpha$, 线段$BD\perp AB$, 且$AB = 7,AC = BD = 24$, 线段$BD与\alpha所成的角为30^{\circ}$, 求$CD$的长.
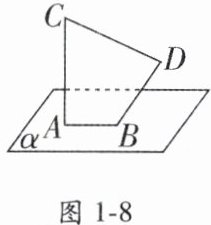

答案:
11.解:如答图1 - 1,由$AC⊥\alpha $,可知$AC⊥AB$,过点D作$DD_{1}⊥\alpha $,$D_{1}$为垂足,连接$BD_{1}$,则$\angle DBD_{1}$为BD与$\alpha $所成的角,即$\angle DBD_{1}=30^{\circ }$,所以$\angle BDD_{1}=60^{\circ }$.因为$AC⊥\alpha ,DD_{1}⊥\alpha $,所以$AC// DD_{1}$,所以$\langle \overrightarrow {CA},\overrightarrow {DB}\rangle =60^{\circ }$,所以$\langle \overrightarrow {CA},\overrightarrow {BD}\rangle =120^{\circ }$.又$\overrightarrow {CD}=\overrightarrow {CA}+\overrightarrow {AB}+\overrightarrow {BD}$,所以$|\overrightarrow {CD}|^{2}=(\overrightarrow {CA}+\overrightarrow {AB}+\overrightarrow {BD})^{2}=|\overrightarrow {CA}|^{2}+|\overrightarrow {AB}|^{2}+|\overrightarrow {BD}|^{2}+2\overrightarrow {CA}\cdot \overrightarrow {AB}+2\overrightarrow {CA}\cdot \overrightarrow {BD}+2\overrightarrow {AB}\cdot \overrightarrow {BD}$.因为$BD⊥AB,AC⊥AB$,所以$\overrightarrow {BD}\cdot \overrightarrow {AB}=0,\overrightarrow {CA}\cdot \overrightarrow {AB}=0$.故$|\overrightarrow {CD}|^{2}=|\overrightarrow {CA}|^{2}+|\overrightarrow {AB}|^{2}+|\overrightarrow {BD}|^{2}+2\overrightarrow {CA}\cdot \overrightarrow {BD}=24^{2}+7^{2}+24^{2}+2×24×24×\cos 120^{\circ }=625$,所以$|\overrightarrow {CD}|=25$.

11.解:如答图1 - 1,由$AC⊥\alpha $,可知$AC⊥AB$,过点D作$DD_{1}⊥\alpha $,$D_{1}$为垂足,连接$BD_{1}$,则$\angle DBD_{1}$为BD与$\alpha $所成的角,即$\angle DBD_{1}=30^{\circ }$,所以$\angle BDD_{1}=60^{\circ }$.因为$AC⊥\alpha ,DD_{1}⊥\alpha $,所以$AC// DD_{1}$,所以$\langle \overrightarrow {CA},\overrightarrow {DB}\rangle =60^{\circ }$,所以$\langle \overrightarrow {CA},\overrightarrow {BD}\rangle =120^{\circ }$.又$\overrightarrow {CD}=\overrightarrow {CA}+\overrightarrow {AB}+\overrightarrow {BD}$,所以$|\overrightarrow {CD}|^{2}=(\overrightarrow {CA}+\overrightarrow {AB}+\overrightarrow {BD})^{2}=|\overrightarrow {CA}|^{2}+|\overrightarrow {AB}|^{2}+|\overrightarrow {BD}|^{2}+2\overrightarrow {CA}\cdot \overrightarrow {AB}+2\overrightarrow {CA}\cdot \overrightarrow {BD}+2\overrightarrow {AB}\cdot \overrightarrow {BD}$.因为$BD⊥AB,AC⊥AB$,所以$\overrightarrow {BD}\cdot \overrightarrow {AB}=0,\overrightarrow {CA}\cdot \overrightarrow {AB}=0$.故$|\overrightarrow {CD}|^{2}=|\overrightarrow {CA}|^{2}+|\overrightarrow {AB}|^{2}+|\overrightarrow {BD}|^{2}+2\overrightarrow {CA}\cdot \overrightarrow {BD}=24^{2}+7^{2}+24^{2}+2×24×24×\cos 120^{\circ }=625$,所以$|\overrightarrow {CD}|=25$.

查看更多完整答案,请扫码查看


