《2025年暑假生活北京师范大学出版社高二数学人教版》

7. 向量$\boldsymbol{a},\boldsymbol{b}$的数量积
两个非零向量$\boldsymbol{a},\boldsymbol{b}$, 则$\boldsymbol{a}\cdot\boldsymbol{b}=$$|\boldsymbol{a}||\boldsymbol{b}|\cos \langle \boldsymbol{a},\boldsymbol{b}\rangle$叫做向量$\boldsymbol{a},\boldsymbol{b}$的数量积(或内积).
同平面向量一样, 空间两个向量的数量积是一个实数, 空间两个向量的数量积也具有如下性质:
(1)$\boldsymbol{a}\perp\boldsymbol{b}\Leftrightarrow$$\boldsymbol{a}\cdot \boldsymbol{b}=0$;
(2)$|\boldsymbol{a}|^{2}=$$\boldsymbol{a}\cdot \boldsymbol{a}$.

答案： 7.$|\boldsymbol{a}||\boldsymbol{b}|\cos \langle \boldsymbol{a},\boldsymbol{b}\rangle$
(1)$\boldsymbol{a}\cdot \boldsymbol{b}=0$
(2)$\boldsymbol{a}\cdot \boldsymbol{a}$

8. 数量积的性质
设$\boldsymbol{a},\boldsymbol{b}$都是非零向量, $\langle\boldsymbol{a},\boldsymbol{b}\rangle=\theta$.
(1)$\boldsymbol{a}//\boldsymbol{b}$时, $\theta=$0或$\pi$. $\theta=$0时, $\boldsymbol{a}与\boldsymbol{b}$同向; $\theta=$$\pi$时, $\boldsymbol{a}与\boldsymbol{b}$反向.
(2)$\boldsymbol{a}\perp\boldsymbol{b}\Leftrightarrow\theta=$$\frac {\pi }{2}$$\Leftrightarrow\boldsymbol{a}\cdot\boldsymbol{b}= 0$.

答案： 8.
(1)0或$\pi$ 0 $\pi$
(2)$\frac {\pi }{2}$

9. 空间向量基本定理
(1) 如果三个向量$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$不共面, 那么对任意一个空间向量$\boldsymbol{p}$, 存在唯一的有序实数组$(x,y,z)$, 使得$\boldsymbol{p}= $$x\boldsymbol{a}+y\boldsymbol{b}+z\boldsymbol{c}$.
(2) 如果三个向量$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$不共面, 那么所有空间向量组成的集合就是$\{\boldsymbol{p}|\boldsymbol{p}= x\boldsymbol{a}+y\boldsymbol{b}+z\boldsymbol{c},x,y,z\in\mathbf{R}\}$, 这个集合可看作是由向量$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$生成的, 我们把( )$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$( )叫做空间的一个基底, $\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$都叫做基向量. 空间任意三个不共面的向量都可构成空间的一个基底. 同一(相等)向量在不同基底下的坐标不同, 在同一基底下的坐标相同.

答案： 9.
(1)$x\boldsymbol{a}+y\boldsymbol{b}+z\boldsymbol{c}$
(2)$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$ 基向量 不共面 不同 相同

【典例1】如图1-2, 已知$E,F,G,H分别是空间四边形ABCD的边AB,BC,CD,DA$的中点. 求证:

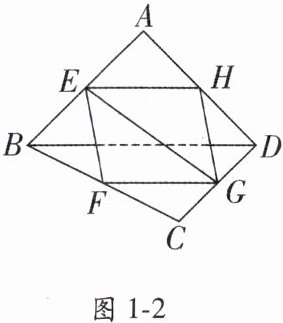
(1)$E,F,G,H$四点共面;
(2)$BD//平面EFGH$.

答案：

证明:
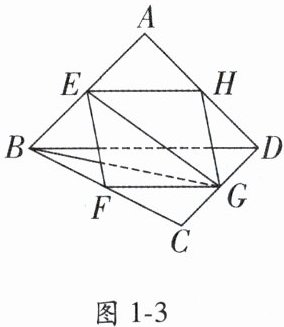
(1) 连接$BG$, 如图1-3,

则$\overrightarrow{EG}= \overrightarrow{EB}+\overrightarrow{BG}$

$=\overrightarrow{EB}+\frac{1}{2}(\overrightarrow{BC}+\overrightarrow{BD})$

$=\overrightarrow{EB}+\overrightarrow{BF}+\overrightarrow{EH}$

$=\overrightarrow{EF}+\overrightarrow{EH}$,

由共面向量定理的推论知$E,F,G,H$四点共面.

(2) 因为$\overrightarrow{EH}= \overrightarrow{AH}-\overrightarrow{AE}= \frac{1}{2}\overrightarrow{AD}-\frac{1}{2}\overrightarrow{AB}= \frac{1}{2}(\overrightarrow{AD}-\overrightarrow{AB})= \frac{1}{2}\overrightarrow{BD}$, 所以$EH// BD$.

又$EH\subset平面EFGH$, $BD\not\subset平面EFGH$,

所以$BD//平面EFGH$.

【典例2】已知$BB_{1}\perp平面ABC$, 且$\triangle ABC是\angle ABC = 90^{\circ}$的等腰直角三角形, $□ ABB_{1}A_{1},□ BB_{1}C_{1}C$的对角线都分别相互垂直且相等, 若$AB = a$, 求异面直线$BA_{1}与AC$所成的角.

答案：

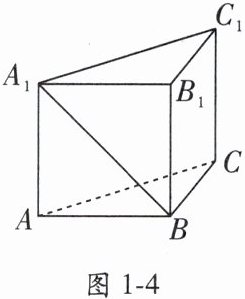
解: 如图1-4.

因为$□ ABB_{1}A_{1},□ BB_{1}C_{1}C$的对角线都分别相互垂直且相等, $\triangle ABC是\angle ABC = 90^{\circ}$的等腰直角三角形, $AB = a$, 所以四边形$ABB_{1}A_{1}和BB_{1}C_{1}C都是边长为a$的正方形, $AC= \sqrt{2}a,BA_{1}= \sqrt{2}a$.

因为$\overrightarrow{BA_{1}}= \overrightarrow{BA}+\overrightarrow{BB_{1}},\overrightarrow{AC}= \overrightarrow{AB}+\overrightarrow{BC}$,

所以$\overrightarrow{BA_{1}}\cdot\overrightarrow{AC}= (\overrightarrow{BA}+\overrightarrow{BB_{1}})\cdot(\overrightarrow{AB}+\overrightarrow{BC})= \overrightarrow{BA}\cdot\overrightarrow{AB}+\overrightarrow{BA}\cdot\overrightarrow{BC}+\overrightarrow{BB_{1}}\cdot\overrightarrow{AB}+\overrightarrow{BB_{1}}\cdot\overrightarrow{BC}$.

因为$AB\perp BC,BB_{1}\perp AB,BB_{1}\perp BC$,

所以$\overrightarrow{BA}\cdot\overrightarrow{BC}= 0,\overrightarrow{BB_{1}}\cdot\overrightarrow{AB}= 0$,

$\overrightarrow{BB_{1}}\cdot\overrightarrow{BC}= 0且\overrightarrow{BA}\cdot\overrightarrow{AB}= -a^{2}$.

所以$\overrightarrow{BA_{1}}\cdot\overrightarrow{AC}= -a^{2}$.

又$\overrightarrow{BA_{1}}\cdot\overrightarrow{AC}= |\overrightarrow{BA_{1}}|\cdot|\overrightarrow{AC}|\cos\langle\overrightarrow{BA_{1}},\overrightarrow{AC}\rangle$,

所以$\cos\langle\overrightarrow{BA_{1}},\overrightarrow{AC}\rangle=\frac{-a^{2}}{\sqrt{2}a\cdot\sqrt{2}a}= -\frac{1}{2}$.

又因为$0^{\circ}\leqslant\langle\overrightarrow{BA_{1}},\overrightarrow{AC}\rangle\leqslant180^{\circ}$,

所以$\langle\overrightarrow{BA_{1}},\overrightarrow{AC}\rangle = 120^{\circ}$.

又因为异面直线所成的角是锐角或直角,

所以异面直线$BA_{1}与AC所成的角为60^{\circ}$.