《2025年暑假生活北京师范大学出版社高二数学人教版》

8. 抛物线的标准方程和几何性质

$y^{2}=2px$$y^{2}=-2px$$x^{2}=2py$$x^{2}=-2py$焦点F到准线l的距离$x=-\frac{p}{2}$$x=\frac{p}{2}$$y=-\frac{p}{2}$$y=\frac{p}{2}$

答案： $y^{2}=2px$ $y^{2}=-2px$ $x^{2}=2py$ $x^{2}=-2py$ 焦点F到准线l的距离 $x=-\frac{p}{2}$ $x=\frac{p}{2}$ $y=-\frac{p}{2}$ $y=\frac{p}{2}$

【典例1】在圆$x^{2}+y^{2}= 4上任取一点P$,设点$P在x轴上的投影为点D$.当点$P$在圆上运动时,动点$M满足\overrightarrow {PD}= 2\overrightarrow {MD}$,动点$M形成的轨迹为曲线C$.求曲线$C$的方程.

答案：

解:方法一 由$\overrightarrow {PD}= 2\overrightarrow {MD}$,知点$M为线段PD$的中点,设点$M的坐标为(x,y)$,则点$P的坐标为(x,2y)$.

因为点$P在圆x^{2}+y^{2}= 4$上,

所以$x^{2}+(2y)^{2}= 4$,

所以曲线$C的方程为\frac {x^{2}}{4}+y^{2}= 1$.

方法二 设点$M的坐标为(x,y)$,点$P的坐标为(x_{0},y_{0})$,

由$\overrightarrow {PD}= 2\overrightarrow {MD}$,得$x_{0}= x,y_{0}= 2y$,

因为点$P(x_{0},y_{0})在圆x^{2}+y^{2}= 4$上,

所以$x_{0}^{2}+y_{0}^{2}= 4,(*)$

把$x_{0}= x,y_{0}= 2y代入(*)$式,得

$x^{2}+4y^{2}= 4$,

所以曲线$C的方程为\frac {x^{2}}{4}+y^{2}= 1$.

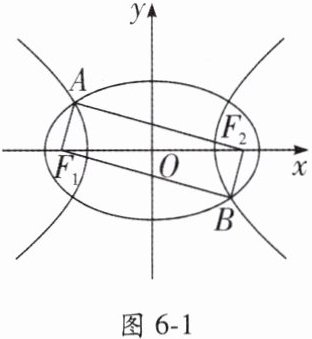
【典例2】如图6-1,$F_{1},F_{2}是椭圆C_{1}:\frac {x^{2}}{4}+y^{2}= 1与双曲线C_{2}$的公共焦点,$A,B分别是C_{1},C_{2}$在第二、四象限的公共点.若四边形$AF_{1}BF_{2}$为矩形,则$C_{2}$的离心率是(D).

A.$\sqrt {2}$
B.$\sqrt {3}$
C.$\frac {3}{2}$
D.$\frac {\sqrt {6}}{2}$

答案：

解析:由椭圆$C_{1}的方程可知|AF_{1}|+|AF_{2}|= 4,|F_{1}F_{2}|= 2\sqrt {3}$.因为四边形$AF_{1}BF_{2}$为矩形,所以$|AF_{1}|^{2}+|AF_{2}|^{2}= |F_{1}F_{2}|^{2}= 12$,所以$2|AF_{1}||AF_{2}|= (|AF_{1}|+|AF_{2}|)^{2}-(|AF_{1}|^{2}+|AF_{2}|^{2})= 16 - 12 = 4$,所以$(|AF_{2}|-|AF_{1}|)^{2}= |AF_{1}|^{2}+|AF_{2}|^{2}-2|AF_{1}||AF_{2}|= 12 - 4 = 8$,所以$|AF_{2}|-|AF_{1}|= 2\sqrt {2}$.设双曲线$C_{2}的方程为\frac {x^{2}}{a^{2}}-\frac {y^{2}}{b^{2}}= 1(a＞0,b＞0)$,则$a= \sqrt {2},c= \sqrt {3}$,所以$C_{2}的离心率e= \frac {c}{a}= \frac {\sqrt {6}}{2}$.

答案:D