《2025年暑假生活北京师范大学出版社高二数学人教版》

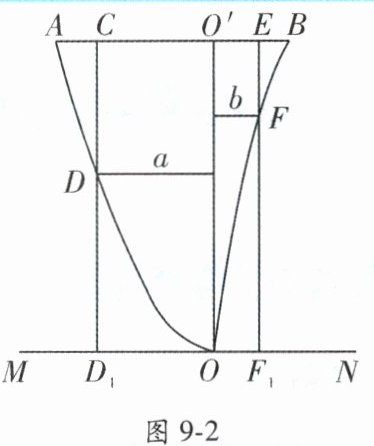
【典例 2】某地准备在山谷中建一座桥梁, 如图 9 - 2 所示, 谷底 $ O $ 在水平线 $ MN $ 上, 桥 $ AB $ 与 $ MN $ 平行, $ OO' $ 为铅垂线 $ (O' $ 在 $ AB $ 上). 经测量, 左侧曲线 $ AO $ 上任一点 $ D $ 到 $ MN $ 的距离 $ h_{1}(m) $ 与 $ D $ 到 $ OO' $ 的距离 $ a(m) $ 之间满足关系式 $ h_{1} = \frac{1}{40}a^{2} $; 右侧曲线 $ BO $ 上任一点 $ F $ 到 $ MN $ 的距离 $ h_{2}(m) $ 与 $ F $ 到 $ OO' $ 的距离 $ b(m) $ 之间满足关系式 $ h_{2} = -\frac{1}{800}b^{3}+6b $. 已知点 $ B $ 到 $ OO' $ 的距离为 $ 40m $.
(1) 求桥 $ AB $ 的长度.
(2) 计划在谷底两侧建造平行于 $ OO' $ 的桥墩 $ CD $ 和 $ EF $, 且 $ CE $ 为 $ 80m $, 其中 $ C $, $ E $ 在线段 $ AB $ 上 (不包含端点). 桥墩 $ EF $ 每米的造价为 $ k $ (万元), 桥墩 $ CD $ 每米的造价为 $ \frac{3}{2}k $ (万元) $ (k \gt 0) $, 问 $ O'E $ 为多少米时, 桥墩 $ CD $ 与 $ EF $ 的总造价最低?

答案：

解:
(1) 过 $ A $, $ B $ 分别作 $ MN $ 的垂线, 垂足分别为 $ A' $, $ B' $, 则 $ AA' = BB' = -\frac{1}{800} × 40^{3}+6 × 40 = 160(m) $.

令 $ \frac{1}{40}a^{2} = 160 $, 得 $ a = 80 $, 所以 $ AO' = 80m $,

$ AB = AO' + BO' = 80 + 40 = 120(m) $.

(2) 设 $ O'E = xm $, 则 $ CO' = (80 - x)m $,

由 $ \begin{cases} 0 \lt x \lt 40, \\ 0 \lt 80 - x \lt 80, \end{cases} $ 得 $ 0 \lt x \lt 40 $.

设总造价为 $ y $ 万元,

则 $ y = \frac{3k}{2}[160 - \frac{1}{40}(80 - x)^{2}] + k[160 - (-\frac{1}{800}x^{3}+6x)] = \frac{k}{800}(x^{3}-30x^{2}+160 × 800) $,

$ y' = \frac{k}{800}(3x^{2}-60x) = \frac{3k}{800}x(x - 20) $.

因为 $ k \gt 0 $, 所以令 $ y' = 0 $, 得 $ x = 0 $ 或 $ x = 20 $,

所以当 $ 0 \lt x \lt 20 $ 时, $ y' \lt 0 $, $ y $ 单调递减;

当 $ 20 \lt x \lt 40 $ 时, $ y' \gt 0 $, $ y $ 单调递增, 所以当 $ x = 20 $ 时, $ y $ 取得最小值, 即当 $ O'E $ 为 $ 20m $ 时, 桥墩 $ CD $ 与 $ EF $ 的总造价最低.