2025年暑假生活北京师范大学出版社高二数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活北京师范大学出版社高二数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 用向量表示点的位置
(1) 向量表示:空间中任意一点 $ P $ 的位置可以用
(2) 点的位置向量:点 $ P $ 的位置向量为
(1) 向量表示:空间中任意一点 $ P $ 的位置可以用
向量$\overrightarrow {OP}$
来表示。(2) 点的位置向量:点 $ P $ 的位置向量为
向量$\overrightarrow {OP}$
。
答案:
1.
(1)向量$\overrightarrow {OP}$
(2)向量$\overrightarrow {OP}$
(1)向量$\overrightarrow {OP}$
(2)向量$\overrightarrow {OP}$
2. 用向量表示直线的位置
|条件|直线 $ l $ 上一点 $ A $|
| |表示直线 $ l $ 方向的向量 $ \boldsymbol{a} $(即直线的
|形式|在直线 $ l $ 上取 $ \overrightarrow{AB} = \boldsymbol{a} $,那么对于直线 $ l $ 上任意一点 $ P $,一定存在实数 $ t $,使得 $ \overrightarrow{AP} = $
|作用|定位置|点 $ A $ 和向量 $ \boldsymbol{a} $ 可以确定直线的
| |定点|可以具体表示出 $ l $ 上的任意
|条件|直线 $ l $ 上一点 $ A $|
| |表示直线 $ l $ 方向的向量 $ \boldsymbol{a} $(即直线的
方向向量
)||形式|在直线 $ l $ 上取 $ \overrightarrow{AB} = \boldsymbol{a} $,那么对于直线 $ l $ 上任意一点 $ P $,一定存在实数 $ t $,使得 $ \overrightarrow{AP} = $
$t\overrightarrow {AB}$
||作用|定位置|点 $ A $ 和向量 $ \boldsymbol{a} $ 可以确定直线的
位置
|| |定点|可以具体表示出 $ l $ 上的任意
一点
|
答案:
2.方向向量 $t\overrightarrow {AB}$ 位置 ⼀点
|位置关系|向量关系|向量运算关系|坐标关系|
| $ l \perp m $|
| $ l \perp \alpha $|
| $ \alpha \perp \beta $|
| $ l \perp m $|
$\boldsymbol{a} \perp \boldsymbol{b}$
|$\boldsymbol{a} \cdot \boldsymbol{b} = 0$
| $ a_1b_1 + a_2b_2 + a_3b_3 = 0 $|| $ l \perp \alpha $|
$\boldsymbol{a} // \boldsymbol{u}$
|$\boldsymbol{a} = \lambda \boldsymbol{u},\lambda \in \mathbf{R}$
| $ a_1 = \lambda u_1 $,$ a_2 = \lambda u_2 $,$ a_3 = \lambda u_3 $|| $ \alpha \perp \beta $|
$\boldsymbol{u} \perp \boldsymbol{v}$
| $ \boldsymbol{u} \cdot \boldsymbol{v} = 0 $| $ u_1v_1 + u_2v_2 + u_3v_3 = 0 $|
答案:
5.$\boldsymbol{a} \perp \boldsymbol{b}$ $\boldsymbol{a} \cdot \boldsymbol{b} = 0$ $\boldsymbol{a} // \boldsymbol{u}$ $\boldsymbol{a} = \lambda \boldsymbol{u},\lambda \in \mathbf{R}$ $\boldsymbol{u} \perp \boldsymbol{v}$
6. 异面直线所成的角
异面直线所成的角的取值范围是 $ \left( 0, \frac{\pi}{2} \right] $,两向量夹角的取值范围是 $ [0, \pi] $,设 $ l_1 $ 与 $ l_2 $ 是两异面直线,$ \boldsymbol{a} $,$ \boldsymbol{b} $ 分别为 $ l_1 $,$ l_2 $ 的方向向量,$ l_1 $,$ l_2 $ 所成的角为 $ \theta $,由向量夹角的定义及求法知 $ \langle \boldsymbol{a}, \boldsymbol{b} \rangle $ 与 $ \theta $ 相等或互补,所以 $ \cos \theta = $
异面直线所成的角的取值范围是 $ \left( 0, \frac{\pi}{2} \right] $,两向量夹角的取值范围是 $ [0, \pi] $,设 $ l_1 $ 与 $ l_2 $ 是两异面直线,$ \boldsymbol{a} $,$ \boldsymbol{b} $ 分别为 $ l_1 $,$ l_2 $ 的方向向量,$ l_1 $,$ l_2 $ 所成的角为 $ \theta $,由向量夹角的定义及求法知 $ \langle \boldsymbol{a}, \boldsymbol{b} \rangle $ 与 $ \theta $ 相等或互补,所以 $ \cos \theta = $
$\frac {|\boldsymbol{a} \cdot \boldsymbol{b}|}{|\boldsymbol{a}| \cdot |\boldsymbol{b}|}$
。
答案:
6.$\frac {|\boldsymbol{a} \cdot \boldsymbol{b}|}{|\boldsymbol{a}| \cdot |\boldsymbol{b}|}$
7. 求直线与平面所成的角
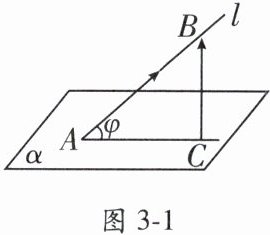
如图 3 - 1,设 $ l $ 为平面 $ \alpha $ 的斜线,$ l \cap \alpha = A $,$ \boldsymbol{a} $ 为 $ l $ 的方向向量,$ \boldsymbol{n} $ 为平面 $ \alpha $ 的法向量,$ \varphi $ 为 $ l $ 与 $ \alpha $ 所成的角,$ \theta = \langle \boldsymbol{a}, \boldsymbol{n} \rangle $,则 $ \sin \varphi = |\cos \theta| = |\cos \langle \boldsymbol{a}, \boldsymbol{n} \rangle| = \frac{|\boldsymbol{a} \cdot \boldsymbol{n}|}{|\boldsymbol{a}| |\boldsymbol{n}|} $。直线与平面所成的角的取值范围是

如图 3 - 1,设 $ l $ 为平面 $ \alpha $ 的斜线,$ l \cap \alpha = A $,$ \boldsymbol{a} $ 为 $ l $ 的方向向量,$ \boldsymbol{n} $ 为平面 $ \alpha $ 的法向量,$ \varphi $ 为 $ l $ 与 $ \alpha $ 所成的角,$ \theta = \langle \boldsymbol{a}, \boldsymbol{n} \rangle $,则 $ \sin \varphi = |\cos \theta| = |\cos \langle \boldsymbol{a}, \boldsymbol{n} \rangle| = \frac{|\boldsymbol{a} \cdot \boldsymbol{n}|}{|\boldsymbol{a}| |\boldsymbol{n}|} $。直线与平面所成的角的取值范围是
$\left[0,\frac{\pi}{2}\right]$
。
答案:
7.$\left[0,\frac{\pi}{2}\right]$
8. 求二面角
平面 $ \alpha $ 与 $ \beta $ 相交于直线 $ l $,平面 $ \alpha $ 的法向量为 $ \boldsymbol{n}_1 $,平面 $ \beta $ 的法向量为 $ \boldsymbol{n}_2 $,$ \langle \boldsymbol{n}_1, \boldsymbol{n}_2 \rangle = \theta $,则二面角 $ \alpha - l - \beta $ 为 $ \theta $ 或 $ \pi - \theta $。设二面角大小为 $ \varphi $,则 $ |\cos \varphi| = |\cos \theta| = $
平面 $ \alpha $ 与 $ \beta $ 相交于直线 $ l $,平面 $ \alpha $ 的法向量为 $ \boldsymbol{n}_1 $,平面 $ \beta $ 的法向量为 $ \boldsymbol{n}_2 $,$ \langle \boldsymbol{n}_1, \boldsymbol{n}_2 \rangle = \theta $,则二面角 $ \alpha - l - \beta $ 为 $ \theta $ 或 $ \pi - \theta $。设二面角大小为 $ \varphi $,则 $ |\cos \varphi| = |\cos \theta| = $
$\frac{|\boldsymbol{n}_1 \cdot \boldsymbol{n}_2|}{|\boldsymbol{n}_1| \cdot |\boldsymbol{n}_2|}$
。二面角的范围是$[0,\pi]$
。
答案:
8.$\frac{|\boldsymbol{n}_1 \cdot \boldsymbol{n}_2|}{|\boldsymbol{n}_1| \cdot |\boldsymbol{n}_2|}$ $[0,\pi]$
查看更多完整答案,请扫码查看


