2025年暑假生活北京师范大学出版社高二数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活北京师范大学出版社高二数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 如图1-5, 在正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中, 下列各式运算的结果为向量$\overrightarrow{AC_{1}}$的共有(
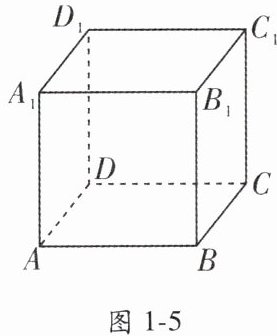
①$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC_{1}}$;
②$\overrightarrow{AA_{1}}+\overrightarrow{A_{1}D_{1}}+\overrightarrow{D_{1}C_{1}}$;
③$\overrightarrow{AB}+\overrightarrow{BB_{1}}+\overrightarrow{B_{1}C_{1}}$;
④$\overrightarrow{AA_{1}}+\overrightarrow{A_{1}B_{1}}+\overrightarrow{B_{1}C_{1}}$.
A.$1$个
B.$2$个
C.$3$个
D.$4$个
D
).
①$\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CC_{1}}$;
②$\overrightarrow{AA_{1}}+\overrightarrow{A_{1}D_{1}}+\overrightarrow{D_{1}C_{1}}$;
③$\overrightarrow{AB}+\overrightarrow{BB_{1}}+\overrightarrow{B_{1}C_{1}}$;
④$\overrightarrow{AA_{1}}+\overrightarrow{A_{1}B_{1}}+\overrightarrow{B_{1}C_{1}}$.
A.$1$个
B.$2$个
C.$3$个
D.$4$个
答案:
1.D 解析:根据空间向量的加法运算法则逐一进行判断:①$\overrightarrow {AB}+\overrightarrow {BC}+\overrightarrow {CC_{1}}=\overrightarrow {AC}+\overrightarrow {CC_{1}}=\overrightarrow {AC_{1}}$;②$\overrightarrow {AA_{1}}+\overrightarrow {A_{1}D_{1}}+\overrightarrow {D_{1}C_{1}}=\overrightarrow {AD_{1}}+\overrightarrow {D_{1}C_{1}}=\overrightarrow {AC_{1}}$;③$\overrightarrow {AB}+\overrightarrow {BB_{1}}+\overrightarrow {B_{1}C_{1}}=\overrightarrow {AB_{1}}+\overrightarrow {B_{1}C_{1}}=\overrightarrow {AC_{1}}$;④$\overrightarrow {AA_{1}}+\overrightarrow {A_{1}B_{1}}+\overrightarrow {B_{1}C_{1}}=\overrightarrow {AB_{1}}+\overrightarrow {B_{1}C_{1}}=\overrightarrow {AC_{1}}$,故所给四个式子的运算结果都是$\overrightarrow {AC_{1}}$.故选D.
2. 设有四边形$ABCD$, $O$为空间任意一点, 且$\overrightarrow{AO}+\overrightarrow{OB}= \overrightarrow{DO}+\overrightarrow{OC}$, 则四边形$ABCD$是(
A.平行四边形
B.空间四边形
C.等腰梯形
D.矩形
A
).A.平行四边形
B.空间四边形
C.等腰梯形
D.矩形
答案:
2.A 解析:因为$\overrightarrow {AO}+\overrightarrow {OB}=\overrightarrow {DO}+\overrightarrow {OC}$,所以$\overrightarrow {AB}=\overrightarrow {DC}$.所以$\overrightarrow {AB}// \overrightarrow {DC}$且$|\overrightarrow {AB}|=|\overrightarrow {DC}|$.所以四边形ABCD为平行四边形.
3. 已知$\boldsymbol{i},\boldsymbol{j},\boldsymbol{k}$是不共面向量, $\boldsymbol{a}= 2\boldsymbol{i}-\boldsymbol{j}+3\boldsymbol{k}$, $\boldsymbol{b}= -\boldsymbol{i}+4\boldsymbol{j}-2\boldsymbol{k}$, $\boldsymbol{c}= 7\boldsymbol{i}+5\boldsymbol{j}+\lambda\boldsymbol{k}$, 若$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$三个向量共面, 则实数$\lambda$等于(
A.$\frac{62}{7}$
B.$9$
C.$\frac{60}{7}$
D.$\frac{65}{7}$
D
).A.$\frac{62}{7}$
B.$9$
C.$\frac{60}{7}$
D.$\frac{65}{7}$
答案:
3.D 解析:因为$\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}$三个向量共面,所以存在实数$m,n$,使得$\boldsymbol{c}=m\boldsymbol{a}+n\boldsymbol{b}$,即$7\boldsymbol{i}+5\boldsymbol{j}+\lambda \boldsymbol{k}=m(2\boldsymbol{i}-\boldsymbol{j}+3\boldsymbol{k})+n(-\boldsymbol{i}+4\boldsymbol{j}-2\boldsymbol{k})$.所以$\begin{cases}7 = 2m - n\\5 = -m + 4n\\\lambda = 3m - 2n\end{cases}$,所以$\lambda = \frac{65}{7}$.故选D.
查看更多完整答案,请扫码查看


