《2025年暑假生活北京师范大学出版社高二数学人教版》

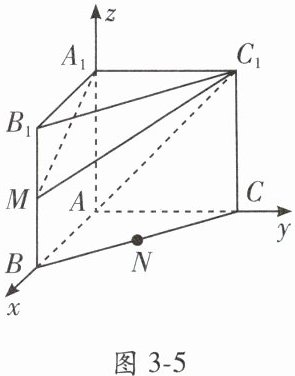
【典例 2】在直三棱柱 $ ABC - A_1B_1C_1 $ 中,$ AB = AC = AA_1 = 2 $,$ \angle BAC = 90^{\circ} $,$ M $ 为 $ BB_1 $ 的中点,$ N $ 为 $ BC $ 的中点。
(1) 求点 $ M $ 到直线 $ AC_1 $ 的距离；
(2) 求点 $ N $ 到平面 $ MA_1C_1 $ 的距离。

答案：

解：
(1) 建立如图 3 - 5 所示的空间直角坐标系,则 $ A(0, 0, 0) $,$ A_1(0, 0, 2) $,$ M(2, 0, 1) $,$ C_1(0, 2, 2) $,直线 $ AC_1 $ 的单位方向向量为 $ \boldsymbol{s}_0 = \left( 0, \frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2} \right) $,$ \overrightarrow{AM} = (2, 0, 1) $,

故点 $ M $ 到直线 $ AC_1 $ 的距离 $ d = \sqrt{|\overrightarrow{AM}|^2 - |\overrightarrow{AM} \cdot \boldsymbol{s}_0|^2} = \sqrt{5 - \frac{1}{2}} = \frac{3\sqrt{2}}{2} $。

(2) 设平面 $ MA_1C_1 $ 的法向量为 $ \boldsymbol{n} = (x, y, z) $,则 $ \boldsymbol{n} \cdot \overrightarrow{A_1C_1} = 0 $ 且 $ \boldsymbol{n} \cdot \overrightarrow{A_1M} = 0 $,即 $ (x, y, z) \cdot (0, 2, 0) = 0 $ 且 $ (x, y, z) \cdot (2, 0, - 1) = 0 $,即 $ y = 0 $ 且 $ 2x - z = 0 $,取 $ x = 1 $,得 $ z = 2 $,故 $ \boldsymbol{n} = (1, 0, 2) $ 为平面 $ MA_1C_1 $ 的一个法向量,与 $ \boldsymbol{n} $ 同向的单位向量为 $ \boldsymbol{n}_0 = \left( \frac{\sqrt{5}}{5}, 0, \frac{2\sqrt{5}}{5} \right) $。

因为 $ N(1, 1, 0) $,所以 $ \overrightarrow{MN} = (- 1, 1, - 1) $,故点 $ N $ 到平面 $ MA_1C_1 $ 的距离 $ d_1 = |\overrightarrow{MN} \cdot \boldsymbol{n}_0| = \frac{3\sqrt{5}}{5} $。