2025年暑假生活北京师范大学出版社高二数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活北京师范大学出版社高二数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
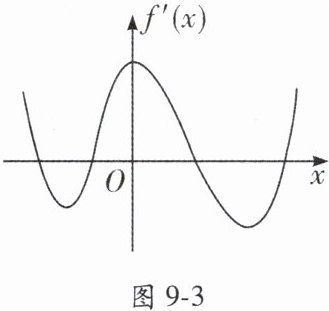
1. 函数 $ f(x) $ 的定义域为 $ R $, 导函数 $ f'(x) $ 的图象如图 9 - 3 所示, 则函数 $ f(x) $ (
A.无极大值点, 有四个极小值点
B.有三个极大值点, 两个极小值点
C.有两个极大值点, 两个极小值点
D.有四个极大值点, 无极小值点
C
).
A.无极大值点, 有四个极小值点
B.有三个极大值点, 两个极小值点
C.有两个极大值点, 两个极小值点
D.有四个极大值点, 无极小值点
答案:
C 解析:若f'(x)在[a,b](x₀∈(a,b))上的符号由正变负,且f'(x₀)=0,则f(x₀)是极大值;若f'(x)在[a,b](x₀∈(a,b))上的符号由负变正,且f'(x₀)=0,则f(x₀)是极小值.由题图易知f(x)有两个极大值点,两个极小值点.
2. 已知函数 $ f(x) = x^{3}+ax^{2}+3x - 9 $, 且 $ f(x) $ 在 $ x = -3 $ 时取得极值, 则实数 $ a $ 等于(
A.5
B.3
C.4
D.2
A
).A.5
B.3
C.4
D.2
答案:
A 解析:因为f'(x)=3x²+2ax+3,所以f'(-3)=3×(-3)²+2a×(-3)+3=0,所以a=5.
3. 已知函数 $ f(x) = x+\frac{1}{x} $, 则 $ f(x) $ (
A.有极大值 2, 极小值 - 2
B.有极大值 - 2, 极小值 2
C.无极大值, 但有极小值 - 2
D.有极大值 2, 但无极小值
B
).A.有极大值 2, 极小值 - 2
B.有极大值 - 2, 极小值 2
C.无极大值, 但有极小值 - 2
D.有极大值 2, 但无极小值
答案:
B 解析:函数的定义域为{x|x≠0},因为f(x)=x+$\frac{1}{x}$,所以f'(x)=1-$\frac{1}{x²}$.令f'(x)=1-$\frac{1}{x²}$=0,得x=±1.当x<-1或x>1时,f'(x)>0;当-1<x<0或0<x<1时,f'(x)<0,所以当x=-1时,函数有极大值-2;当x=1时,函数有极小值2.
4. 下列说法正确的是(
A.函数在其定义域内若有最值与极值, 则其极大值便是最大值, 极小值便是最小值
B.闭区间上的连续函数一定有最值, 也一定有极值
C.若函数在其定义域上有最值, 则一定有极值; 反之, 若有极值, 则一定有最值
D.若函数在给定区间上有最大 (小) 值, 则有且仅有一个最大 (小) 值, 但若有极值, 则可能有多个极值
D
).A.函数在其定义域内若有最值与极值, 则其极大值便是最大值, 极小值便是最小值
B.闭区间上的连续函数一定有最值, 也一定有极值
C.若函数在其定义域上有最值, 则一定有极值; 反之, 若有极值, 则一定有最值
D.若函数在给定区间上有最大 (小) 值, 则有且仅有一个最大 (小) 值, 但若有极值, 则可能有多个极值
答案:
D 解析:由极值与最值的区别知选D.
5. 函数 $ f(x) = e^{x}-x $ 在区间 $ [-1,1] $ 上的最大值是(
A.$ 1+\frac{1}{e} $
B.1
C.$ e - 1 $
D.$ e + 1 $
C
).A.$ 1+\frac{1}{e} $
B.1
C.$ e - 1 $
D.$ e + 1 $
答案:
C 解析:由题意得f'(x)=eˣ-1.令f'(x)=0,得x=0.当x∈[-1,0)时,f'(x)<0;当x∈(0,1]时,f'(x)>0,所以f(x)在[-1,0)上单调递减,在(0,1]上单调递增.又因为f(-1)=$\frac{1}{e}$+1,f
(1)=e-1,所以f(-1)-f
(1)=2+$\frac{1}{e}$-e<0,所以f(-1)<f
(1),所以f(x)max=f
(1)=e-1.
(1)=e-1,所以f(-1)-f
(1)=2+$\frac{1}{e}$-e<0,所以f(-1)<f
(1),所以f(x)max=f
(1)=e-1.
6. 若函数 $ y = x^{3}+\frac{3}{2}x^{2}+m $ 在 $ [-2,1] $ 上的最大值为 $ \frac{9}{2} $, 则实数 $ m $ 等于(
A.0
B.2
C.$ \frac{5}{2} $
D.1
B
).A.0
B.2
C.$ \frac{5}{2} $
D.1
答案:
B 解析:y'=(x³+$\frac{3}{2}$x²+m)'=3x²+3x=3x(x+1),令y'=0,得x=0或x=-1.设y=f(x)=x³+$\frac{3}{2}$x²+m,则f
(0)=m,f(-1)=m+$\frac{1}{2}$.又因为f
(1)=m+$\frac{5}{2}$,f(-2)=-8+6+m=m-2,所以f
(1)=m+$\frac{5}{2}$最大,所以m+$\frac{5}{2}$=$\frac{9}{2}$,所以m=2.
(0)=m,f(-1)=m+$\frac{1}{2}$.又因为f
(1)=m+$\frac{5}{2}$,f(-2)=-8+6+m=m-2,所以f
(1)=m+$\frac{5}{2}$最大,所以m+$\frac{5}{2}$=$\frac{9}{2}$,所以m=2.
7. (多选) 已知定义在 $ R $ 上的函数 $ f(x) $, 其导函数 $ f'(x) $ 的大致图象如图 9 - 4 所示, 则下列叙述不正确的有(
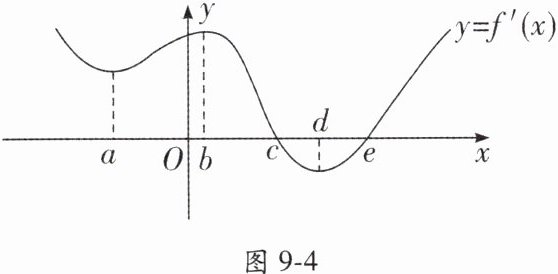
A.$ f(a) \gt f(e) \gt f(d) $
B.函数 $ f(x) $ 在 $ [a,b] $ 上单调递增, 在 $ [b,d] $ 上单调递减
C.函数 $ f(x) $ 的极值点为 $ c,e $
D.函数 $ f(x) $ 的极大值为 $ f(b) $
ABD
).
A.$ f(a) \gt f(e) \gt f(d) $
B.函数 $ f(x) $ 在 $ [a,b] $ 上单调递增, 在 $ [b,d] $ 上单调递减
C.函数 $ f(x) $ 的极值点为 $ c,e $
D.函数 $ f(x) $ 的极大值为 $ f(b) $
答案:
ABD 解析:由题图可知,当x∈(-∞,c)时,f'(x)>0;当x∈(c,e)时,f'(x)<0;当x∈(e,+∞)时,f'(x)>0,所以f(x)在(-∞,c)上单调递增,在(c,e)上单调递减,在(e,+∞)上单调递增,所以f(d)>f(e),故A中叙述错误;函数f(x)在[a,b]上单调递增,在[b,c]上单调递增,在[c,d]上单调递减,故B中叙述错误;函数f(x)的极值点为c,e,故C中叙述正确;函数f(x)的极大值为f(c),故D中叙述错误.
8. 用边长为 $ 48cm $ 的正方形铁皮做一个无盖的铁盒时, 在铁皮的四角各截去一个面积相等的小正方形, 然后把四边折起, 就能焊成铁盒, 所做的铁盒容积最大时, 在四角截去的小正方形的边长为
8
cm.
答案:
8 解析:设截去的小正方形的边长为x cm,铁盒的容积为V cm³,则铁盒的底面边长为(48-2x)cm.由题意,得V=x(48-2x)²(0<x<24),V'=12x²-384x+2304=12(x-8)(x-24).因为0<x<24,所以当x=8时,Vmax=8192.
查看更多完整答案,请扫码查看


