《2025年创新成功学习快乐暑假七年级》

23. 计算：$x^{2}-(x+3)(x-3).$

答案： 解：原式 $=x^{2}-(x^{2}-9)$
$=x^{2}-x^{2}+9$
$=9$

24. 先化简,再求值:$x(x-y)-(x+1)^{2}+2x$,其中$x= -\frac {1}{2025},y= 2025.$
解：原式 $= x^{2} - xy - x^{2} - 2x - 1 + 2x $
$= $$-xy - 1$，
当 $ x = -\frac{1}{2025} $，$ y = 2025 $ 时，原式 $= $$0$。

答案： 解：原式 $ = x^{2} - xy - x^{2} - 2x - 1 + 2x $
$ = -xy - 1 $，
当 $ x = -\frac{1}{2025} $，$ y = 2025 $ 时，原式 $ = 1 - 1 = 0 $。

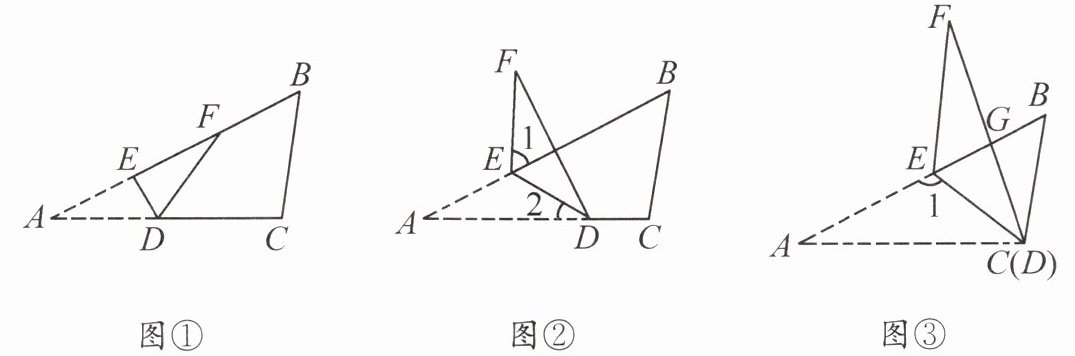
25. 小星在学习了轴对称的性质后,对三角形中各角之间的关系进行了拓展探究. 如图,在$△ABC$中,将$△ABC$沿 DE 折叠,点 A 的对应点是点 F.
(1)问题解决:如图①,$∠A= 30^{\circ }$,当点 A 的对应点 F 落在$△ABC$的 AB 边上时,$∠DFE= $$30^{\circ}$;
(2)问题探究:如图②,$∠A= 30^{\circ }$,当点 A 的对应点 F 落在$△ABC$的外部时,若$∠1= 40^{\circ }$,求$∠2$的度数;
(3)拓展延伸:如图③,当点 C 与点 D 重合时,将$△ABC$沿 CE 折叠. 点 A 的对应点是点 F,CF 与 EB 相交于点 G,若 G 是 BE 的中点,$S_{△ACE}= S_{△BCE},∠1= 115^{\circ }$. 求$∠B$的度数.

答案：
(1) $ 30^{\circ} $
解：
(2)题图②中，设 $ \angle 2 = x $。
∵ $ \angle BED = \angle A + \angle 2 $，$ \angle A = 30^{\circ} $，
∴ $ \angle BED = 30^{\circ} + x $。
由翻折变换的性质可知，$ \angle AED = \angle FED = 40^{\circ} + 30^{\circ} + x = 70^{\circ} + x $，
∵ $ \angle A + \angle AED + \angle 2 = 180^{\circ} $，
∴ $ 30^{\circ} + x + 70^{\circ} + x = 180^{\circ} $。
∴ $ x = 40^{\circ} $。
∴ $ \angle 2 = 40^{\circ} $。
(3)如题图③中，连接 $ AF $，$ BF $，延长 $ CE $ 交 $ AF $ 于点 $ T $。
由翻折变换的性质可知，$ CT \perp AF $，$ \angle 1 = \angle FEC = 115^{\circ} $，
∴ $ \angle CEB = 180^{\circ} - \angle 1 = 65^{\circ} $。
∴ $ \angle BEF = \angle FEC - \angle CEB = 115^{\circ} - 65^{\circ} = 50^{\circ} $。
∵ $ S_{\triangle ACE} = S_{\triangle BCE} $，点 $ C $ 到 $ AB $ 的距离不变，
∴ $ AE = EB = EF $。
∴ $ \angle EAF = \angle EFA $，$ \angle EBF = \angle EFB $，
∵ $ \angle FAB + \angle AFB + \angle FBA = 180^{\circ} $，
∴ $ 2 \angle AFE + 2 \angle EFB = 180^{\circ} $。
∴ $ \angle AFE + \angle EFB = 90^{\circ} $。
∴ $ \angle AFB = \angle ATE = 90^{\circ} $。
∴ $ ET // BF $。
∴ $ \angle BFG = \angle ECG $。
∵ $ \angle FGB = \angle CGE $，$ BG = EG $，
∴ $ \triangle BGF \cong \triangle EGC (AAS) $。
∴ $ FG = GC $，
∵ $ EG = GB $，$ \angle FGE = \angle CGB $，
∴ $ \triangle FGE \cong \triangle CGB $。
∴ $ \angle GBC = \angle GEF = 50^{\circ} $。