《2025年创新成功学习快乐暑假七年级》

14. 弹簧挂上物体后会伸长,测得一弹簧的长度 $ y(\mathrm{cm}) $ 与所挂的物体的质量 $ x(\mathrm{kg}) $ 间有如表的关系 (弹簧的弹性范围 $ x \leq 10 \mathrm{kg} $),则下列说法

不

正

确

的是 (D)
| $ x $ | 0 | 2 | 4 | 6 | 8 | 10 |
| $ y $ | 10 | 10.5 | 11 | 11.5 | 12 | 12.5 |

A.$ x $ 与 $ y $ 都是变量,且 $ x $ 是自变量,$ y $ 是因变量
B.弹簧不挂重物时的长度为 $ 10 \mathrm{cm} $
C.所挂物体质量为 $ 5 \mathrm{kg} $ 时,弹簧长度增加了 $ 1.25 \mathrm{cm} $
D.所挂物体质量为 $ 9 \mathrm{kg} $ 时,弹簧长度增加到 $ 11.25 \mathrm{cm} $

答案： D

15. 计算 $ x(x - 1) $ 的结果是 $ x^{2}-x $。

答案： $ x^{2}-x $

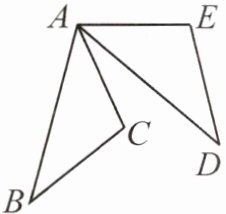
16. 如图,$ AB = AD $,$ AC = AE $,若要添加一个条件,使 $ \triangle ABC \cong \triangle ADE $,则添加的条件是 $ BC = DE $ 或 $ ∠BAC = ∠DAE $ 或 $ ∠BAD = ∠CAE $。(写一个条件即可)

答案： $ BC = DE $ 或 $ ∠BAC = ∠DAE $ 或 $ ∠BAD = ∠CAE $

17. 一个不透明的袋子中装有 3 个球,分别标有 1,2,$ x $ 这三个号码,这 3 个球除号码外都相同. 搅匀后任意摸出一个球,摸到号码是 1 的球概率为 $ \frac{2}{3} $,则号码 $ x $ 的值是 1。

答案： 1

18. 若 $ m^2 - n^2 = 30 $,且 $ m - n = 6 $,则 $ m + n = $5。

答案： 5

19. 如果 $ |m - 3| + (n + 2)^2 = 0 $,那么 $ -5x^m y^{-n} + 7x^3 y^2 = $ $ 2x^{3}y^{2} $。

答案： $ 2x^{3}y^{2} $

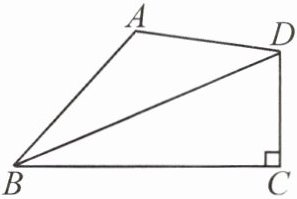
20. 如图,在四边形 $ ABCD $ 中,$ \angle BCD = 90^{\circ} $,$ BD $ 平分 $ \angle ABC $,$ AB = 6 $,$ BC = 8 $,$ CD = 4 $,则四边形 $ ABCD $ 的面积是 28。

答案： 28

21. 如图,一牧民从点 $ A $ 出发,到草地 $ MN $ 去喂马,该牧民在傍晚回到营帐 $ B $ 之前先带马去小河边 $ PQ $ 给马饮水 ($ MN $,$ PQ $ 均为直线),试问牧民应走怎样的路线,才能使整个路程最短？ (简要说明作图步骤,并在图上画出)

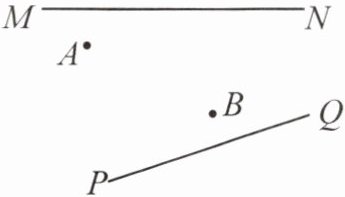
答案：
解:如图,①作点A关于MN的对称点A',作点B关于PQ的对称点B',②连接A'B',交MN于点C,交PQ于点D,③连接AC,CD,BD.则折线ACDB是牧民所走的最短路线.