《2025年暑假生活新疆文化出版社八年级数学冀教版》

1. 对于平面上的任意一点,都有唯一一对______与它对应；反过来,对任意一对______,都有平面上唯一的一点与它对应,这就是说,在______平面上,点和有序实数是______的。

答案： 有序实数 有序实数 坐标 一一对应

2. 直角坐标系的横轴与纵轴将平面分成了______个部分,从右上方的部分说起,按逆时针方向,各部分依次叫做______、______、______和______,______上的点不属于任何一个象限。

答案： 四 第一象限 第二象限 第三象限 第四象限 坐标轴

3. 点的坐标特点：
(1)象限内的点的坐标特点：点 $ P(x,y) $ 在第一象限,则 $ x＞0,y＞0 $；在第二象限,则 $ x $______ $ 0,y $______ $ 0 $；在第三象限,则 $ x＜0,y $______ $ 0 $；在第四象限,则 $ x＞0,y $______ $ 0 $。反之亦然。
(2)坐标轴上点的坐标特点：点 $ P(x,y) $ 在 $ x $ 轴上,则 $ x $______,$ y= 0 $；点 $ P $ 在 $ y $ 轴上,则 $ x $______,$ y $ 为任意实数。

答案：
(1) ＜ ＞ ＜ ＜
(2) 为任意实数 =0

4. 如果点 $ P $ 的坐标为 $ (x,y) $,则点 $ P $ 关于 $ x $ 轴对称的点 $ P_1 $ 的坐标为______；点 $ P $ 关于 $ y $ 轴对称的点 $ P_2 $ 的坐标为______；点 $ P $ 关于原点对称的点 $ P_3 $ 的坐标为______。

答案： (x,-y) (-x,y) (-x,-y)

5. 平移图形的坐标特征
(1)在直角坐标系中,对于坐标平面上任意一点 $ P(x,y) $,将它沿 $ x $ 轴的方向向右(或向左)平移 $ k $ 个单位长度,相当于这个点的横坐标______,纵坐标______。
(2)将点 $ P(x,y) $ 沿 $ y $ 轴方向向上(或向下)平移 $ k $ 个单位长度,相当于这个点的横坐标______,纵坐标______。

答案：
(1) 增加(或减少)k 不变
(2) 不变 增加(或减少)k

【例 1】如图,在中国象棋的残局上建立平面直角坐标系,如果“相”和“兵”的坐标分别是 $ (3,-1) $ 和 $ (-3,1) $,那么“卒”的坐标为______。

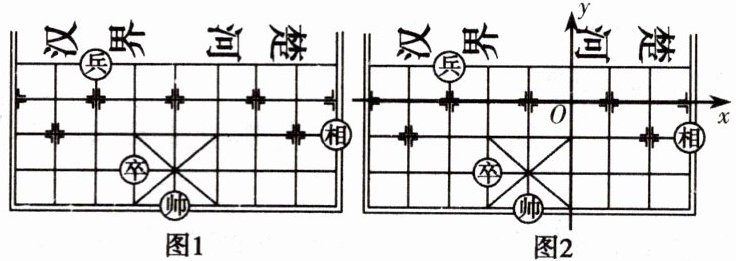
【解析】首先根据“相”和“兵”的坐标确定原点位置,然后建立如图 2 所示的坐标系,进而可得“卒”的坐标为 $ (-2,-2) $。故填 $ (-2,-2) $。
【答案】$ (-2,-2) $

答案：

1. 小强向同学们介绍图书馆的位置时,其中表达正确的是 ( )

A.在学校的右边
B.距学校 1000 米处
C.在学校的西边
D.在学校的西边距学校 1000 米处

答案： D