《2025年暑假生活新疆文化出版社八年级数学冀教版》

【例3】 如图所示,$M$、$N分别是□ ABCD的对边AD$、$BC$的中点,$AN与BM交于点P$,$CM与DN交于点Q$,$AD = 2AB$,求证：四边形$PMQN$是矩形.
【解析】
1. 用定义判定一个四边形是矩形必须满足两个条件：一是有一个角是直角；二是平行四边形,也就是说有一个角是直角的四边形不一定是矩形,必须加上“平行四边形”这个条件,它才是矩形.
2. 用方法1判定一个四边形是矩形,也必须满足两个条件：一是对角线相等；二是平行四边形,也就是说,两条对角线相等的四边形不一定是矩形,必须加上“平行四边形”这个条件,它才是矩形.
证明：$\because点M$、$N分别是□ ABCD的对边AD$、$BC$的中点,$\therefore四边形AMCN$、四边形$MDNB$,四边形$ABNM$均分平行四边形,$\therefore PN// MQ$,$PM// NQ$,$\therefore四边形PNQM$为平行四边形,$\because AD = 2AB$,$M是AD$的中点,$\therefore AM = AB$,$\therefore四边形ABNM$为菱形,$\therefore AN\perp BM$,即$\angle MPN = 90^{\circ}$,$\therefore四边形PMQN$是矩形.

答案：

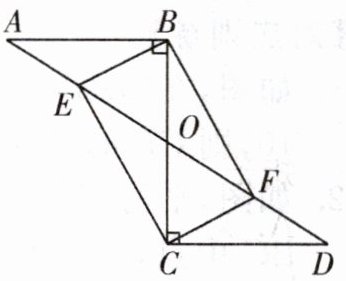
4. 如图,$AD和BC相交于点O$,$\angle ABO = \angle DCO = 90^{\circ}$,$OB = OC$,点$E$,$F分别是AO$,$DO$的中点.
(1)求证：$OE = OF$；
(2)当$\angle A = 30^{\circ}$时,求证：四边形$BECF$是矩形.

答案： 4. 证明：
(1)在$\triangle AOB$与$\triangle DOC$中，$\left\{\begin{array}{l} ∠ABO=∠DCO=90^{\circ }\\ OB=OC\\ ∠AOB=∠DOC\end{array}\right. $ $\therefore \triangle AOB\cong \triangle DOC(ASA),\therefore OA=OD$，又$\because E,F$分别是$AO,DO$中点，$\therefore OE=\frac {1}{2}OA,OF=\frac {1}{2}OD,\therefore OE=OF$.
(2)$\because OB=OC,OF=OE,\therefore $四边形 BECF 是平行四边形，$\because BC=2OB,EF=2OE.\because E$为$AO$的中点，$∠ABO=90^{\circ },\therefore EB=EO=EA$(提示：直角三角形中斜边中线等于斜边的一半).$\because ∠A=30^{\circ },\therefore ∠BOE=60^{\circ },\therefore \triangle BOE$是等边三角形，$\therefore OB=OE,\therefore BC=EF,\therefore $平行四边形 BECF 是矩形.

【例4】 如图,在菱形$ABCD$中,对角线$AC$、$BD相交于点O$,$E为BC$的中点,则下列式子中一定成立的是 ( )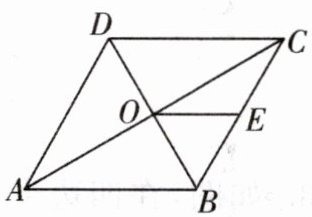
A. $AC = 2OE$
B. $BC = 2OE$
C. $AD = OE$
D. $OB = OE$
【解析】
1. 菱形的定义有两个要素：(1)是平行四边形；(2)有一组邻边相等. 菱形的定义既是菱形的一条性质,也是菱形的一种判定方法.
2. 菱形的两条对角线所在的直线是菱形的对称轴,菱形被两条对角线所分得的四个直角三角形全等.
3. 菱形的面积$=底×高= $对角线乘积的一半.
解：$\because菱形ABCD$,$\therefore AB = BC$,$OA = OC$,$\because E为BC$的中点,$\therefore OE为\triangle ABC$的中位线,$OE = \frac{1}{2}AB$,$BC = 2OE$.
【答案】 $B$

答案：