《2025年暑假生活新疆文化出版社八年级数学冀教版》

5. 如图,直线$y= -x-4$交x轴和y轴于点A和点C,点$B(0,2)$在y轴上,作直线AB,点P为直线AB上一动点.
(1)直线AB的表达式为____;
(2)当$∠BCP= ∠BAO$时,求直线CP的表达式及CP的长.

答案：
解:
(1)
∵直线$y = -x - 4$交 x 轴和 y 轴于点 A 和点 C,
∴ 点$A(-4,0)$,点$C(0,-4)$. 设直线 AB 的表达式为$y = kx + b$,由题意可得$\begin{cases} b = 2 \\ 0 = -4k + b \end{cases}$,解得$\begin{cases} k=\frac{1}{2} \\ b = 2 \end{cases}$,
∴ 直线 AB 的表达式为$y=\frac{1}{2}x + 2$,故答案为$y=\frac{1}{2}x + 2$.
(2)如图,当点 P 在线段 AB 上时,设 CP 与 AO 交于点 H. 在$△AOB$和$△COH$中,$\begin{cases} ∠AOB = ∠COH \\ AO = CO \\ ∠BAO = ∠PCB \end{cases}$,$\therefore △AOB≌△COH(ASA)$,$\therefore OH = OB = 2$,
∴ 点 H 坐标为$(-2,0)$. 设直线 PC 的表达式为$y = ax + c$,由题意可得$\begin{cases} c = -4 \\ 0 = -2a + c \end{cases}$,解得$\begin{cases} a = -2 \\ c = -4 \end{cases}$,
∴ 直线 PC 表达式为$y = -2x - 4$,联立得$\begin{cases} y = -2x - 4 \\ y=\frac{1}{2}x + 2 \end{cases}$解得$\begin{cases} x = -\frac{12}{5} \\ y=\frac{4}{5} \end{cases}$,$\therefore$点$P(-\frac{12}{5},\frac{4}{5})$,$\therefore CP=\sqrt{(-\frac{12}{5}-0)^{2}+(\frac{4}{5}+4)^{2}}=\frac{12\sqrt{5}}{5}$;如图,当点$P(P')$在 AB 延长线上时,设$CP'$与 x 轴交于点$H'$,同理可得直线$P'C$的表达式为$y = 2x - 4$,联立得$\begin{cases} y = 2x - 4 \\ y=\frac{1}{2}x + 2 \end{cases}$,解得$\begin{cases} x = 4 \\ y = 4 \end{cases}$,$\therefore$点$P'(4,4)$,$\therefore CP'=\sqrt{(4 - 0)^{2}+(4 + 4)^{2}}=4\sqrt{5}$. 综上所述, 直线 CP 的表达式为$y = -2x - 4$或$y = 2x - 4$,CP 的长为$\frac{12\sqrt{5}}{5}$或$4\sqrt{5}$.

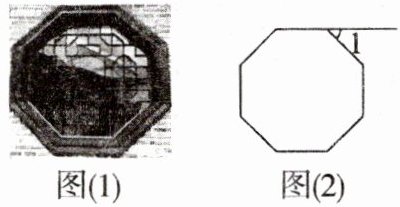
1. 如图(1)是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中,如图(2)是八角形空窗的示意图,它的一个外角$∠1= $ ( )


A.$45^{\circ}$
B.$60^{\circ}$
C.$110^{\circ}$
D.$135^{\circ}$

答案： A

2. 象棋起源于中国,中国象棋文化历史悠久.如图所示是某次对弈的残图,如果建立平面直角坐标系,使棋子“帅”位于点$(-2,-1)$的位置,则在同一坐标系下,经过棋子“帅”和“马”所在的点的一次函数表达式为 ( )


A.$y= x+1$
B.$y= x-1$
C.$y= 2x+1$
D.$y= 2x-1$

答案： A