《2025年暑假生活新疆文化出版社八年级数学冀教版》

5. 在如图的平面直角坐标系中,四边形$ABCD各顶点的坐标分别是A(0,0)$,$B(9,0)$,$C(7,5)$,$D(2,7)$.试求这个图形的面积.

答案：
解:如图,分别过点 D,C 向 x 轴作垂线,垂足分别为点 E,F,则四边形 ABCD 被分割为$\triangle AED$,$\triangle BCF$及梯形 CDEF.由各点的坐标可得$AE = 2$,$DE = 7$,$EF = 5$,$FB = 2$,$CF = 5$,所以$S_{四边形ABCD} = S_{\triangle AED} + S_{梯形CDEF} + S_{\triangle CFB} = \frac{1}{2}× 2× 7 + \frac{1}{2}× (7 + 5)× 5 + \frac{1}{2}× 5× 2 = 7 + 30 + 5 = 42$.

6. 如图,在四边形$ABCD$中,$∠C = 90^{\circ}$,$∠ABD = ∠CBD$,$AB = CB$,$P是BD$上一点,$PE⊥BC$,$PF⊥CD$,垂足分别为点$E,F$. 求证:$PA = EF$.

答案： 证明:连接 PC.$\because PE\perp BC$,$PF\perp CD$,$\angle ECF = 90^{\circ}$,$\therefore \angle PEC = \angle PFC = \angle ECF = 90^{\circ}$.$\therefore$四边形 PECF 是矩形.$\therefore PC = EF$.在$\triangle ABP$和$\triangle CBP$中,$\left\{\begin{array}{l}AB = CB,\\ \angle ABP = \angle CBP,\\ BP = BP,\end{array}\right.$$\therefore \triangle ABP\cong \triangle CBP(SAS)$,$\therefore PA = PC$,$\therefore PA = EF$.

7. 从如图的五边形$ABCDE$纸片中剪去一个三角形,剩余部分的多边形的内角和是____.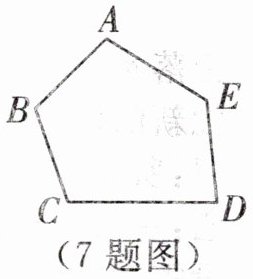

答案：
$360^{\circ}$或$540^{\circ}$或$720^{\circ}$【点拨】从一个五边形中剪去一个三角形,得到的多边形可能是四边形、可能是五边形、可能是六边形,分三种情况:①若剩余部分的多边形是四边形,则内角和为$360^{\circ}$;②若剩余部分的多边形是五边形,则内角和为$(5 - 2)× 180^{\circ} = 540^{\circ}$;③若剩余部分的多边形是六边形,则内角和为$(6 - 2)× 180^{\circ} = 720^{\circ}$.

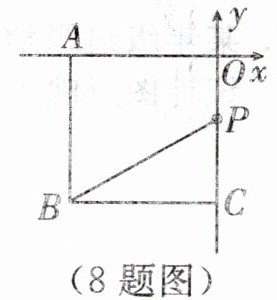
8. 如图,在平面直角坐标系中,四边形$OABC$是边长为4的正方形,$A点在x$轴负半轴上,$C点在y$轴负半轴上.有一动点$P自O$点出发,以每秒2个单位长度的速度沿$O→A→B→C→O运动到O$点后停止,则何时$S_{△PBC}= 4$? 并求出此时$P$点的坐标.

答案： 解:设点 P 的运动时间为$t$秒.
(1)当 P 在 OA 上运动时,$S_{\triangle PBC} = \frac{1}{2}× 4× 4 = 8\neq 4$。
(2)当 P 在 AB 上运动时,$S_{\triangle PBC} = \frac{1}{2}PB\cdot BC$,若$S_{\triangle PBC} = 4$,则$PB = 2$,此时$OA + AP = OA + AB - PB = 4 + 4 - 2 = 6$,$P(-4,-2)$.所以$t = \frac{6}{2} = 3$。
(3)当 P 在 BC 上运动时,P,B,C 不能构成三角形,不成立。
(4)当 P 在 CO 上运动时,$S_{\triangle PBC} = \frac{1}{2}PC\cdot BC$,若$S_{\triangle PBC} = 4$,则$PC = 2$,所以$PO = 2$.所以$t = \frac{OA + AB + BC + PC}{2} = \frac{4 + 4 + 4 + 2}{2} = 7$,$P(0,-2)$.综上,经过 3 秒或 7 秒时,$S_{\triangle PBC} = 4$,对应的点 P 的坐标分别为$(-4,-2)$,$(0,-2)$。

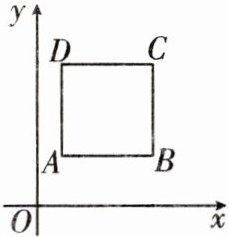
9. 在如图所示的平面直角坐标系中,四边形$ABCD$是正方形,且顶点$A,B的坐标分别为(1,2)$,$(5,2)$.
(1)点$C$的坐标为____,点$D$的坐标为____;
(2)若一次函数$y = ax - 4(a≠0)的图象经过点C$,求函数表达式;
(3)若(2)中函数的图象与$x轴交于点E$,画出图象,连接$OC$,并求$△OCE$的面积;
(4)若直线$y = kx + b$与(2)中的函数图象平行且位于$B,D$两点之间(包含$B,D$两点),求$b$的范围.

答案：
解:
(1)$(5,6)$;$(1,6)$
(2)因为一次函数$y = ax - 4(a\neq 0)$的图象经过点 C,所以将点$C(5,6)$的坐标代入$y = ax - 4$,得$6 = 5a - 4$,解得$a = 2$.所以$y = 2x - 4$。
(3)在$y = 2x - 4$中,令$y = 0$,得$2x - 4 = 0$,解得$x = 2$,所以$E(2,0)$.所画图象为直线 CE,如图所示.易得$S_{\triangle OCE} = \frac{1}{2}× 2× 6 = 6$。
(4)由题意知,直线$y = kx + b$与直线$y = 2x - 4$平行,则$k = 2$,所以$y = 2x + b$.若直线$y = 2x + b$过点$B(5,2)$,则$2× 5 + b = 2$,解得$b = - 8$;若直线$y = 2x + b$过点$D(1,6)$,则$2× 1 + b = 6$,解得$b = 4$,所以________$\leq b\leq$________且$b\neq$________。