7. 如图,在菱形$ABCD$中,对角线$AC$,$BD相交于点O$,$BD= 8$,$AC= 6$,$OE// AB$,交$BC于点E$,则$OE$的长为______。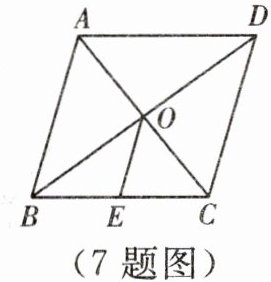

答案:
$\frac{5}{2}$
8. 如图,在四边形$ABCD$中,$AB= 10$,$BD\perp AD$。若将$\triangle BCD沿BD$折叠,点$C与边AB的中点E$恰好重合,则四边形$BCDE$的周长为______。
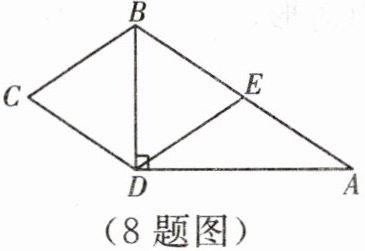

答案:
20
9. 如图,正五边形$ABCDE$中,连接$AC$,那么$\angle BAC$的度数为______。
答案:
$36^{\circ}$
10. 如图,在平面直角坐标系中,点$A的坐标为(9,0)$,点$C的坐标为(0,3)$,以$OA$,$OC为边作矩形OABC$。动点$E$,$F分别从点O$,$B$同时出发,以每秒1个单位长度的速度沿$OA$,$BC向终点A$,$C$移动。当移动时间为4秒时,$AC\cdot EF$的值为( )

A. $\sqrt{10}$
B. $9\sqrt{10}$
C. 15
D. 30

A. $\sqrt{10}$
B. $9\sqrt{10}$
C. 15
D. 30
答案:
30
11. (本小题满分14分)
如图所示,将平行四边形纸片$ABCD$按如图所示的方式折叠,使点$C与点A$重合,点$D落在D'$处,折痕为$EF$。求证:四边形$AECF$是菱形。
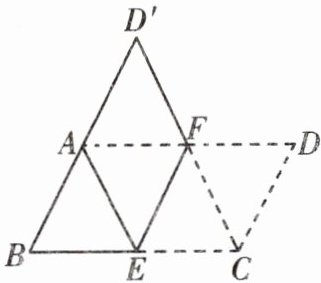
如图所示,将平行四边形纸片$ABCD$按如图所示的方式折叠,使点$C与点A$重合,点$D落在D'$处,折痕为$EF$。求证:四边形$AECF$是菱形。

答案:
由折叠的性质可得 $AE = EC$,$AF = CF$,$\angle AEF = \angle CEF$,又 $AD // BC$,$\therefore \angle AFE = \angle CEF$,$\therefore \angle AEF = \angle AFE$,$\therefore AE = AF$,$\therefore AE = EC = CF = AF$,$\therefore$ 四边形 $AECF$ 是菱形
由折叠的性质可得 $AE = EC$,$AF = CF$,$\angle AEF = \angle CEF$,又 $AD // BC$,$\therefore \angle AFE = \angle CEF$,$\therefore \angle AEF = \angle AFE$,$\therefore AE = AF$,$\therefore AE = EC = CF = AF$,$\therefore$ 四边形 $AECF$ 是菱形

查看更多完整答案,请扫码查看


