《2025年暑假生活新疆文化出版社八年级数学冀教版》

16. 若一个正多边形的每个内角为144°,则这个正多边形的边数是______.

答案： 10

17. 已知某个一次函数的图象如图所示,则该函数的解析式为______.

答案： y = 2x + 2

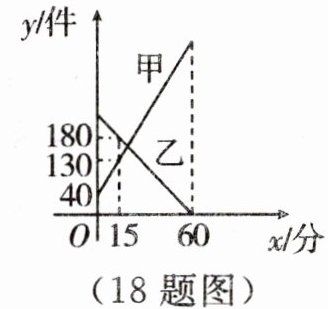
18. 某快递公司每天上午7:00—8:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法：
①15分钟后,甲仓库内快件数量为180件；
②乙仓库每分钟派送件数量为4件；
③8:00时,甲仓库内快件数为600件；
④7:20时,两仓库快递数相同.
其中正确的序号为______.

答案： ②④

19. (本小题满分8分)已知：如图,把三角形ABC向上平移3个单位长度,再向右平移2个单位长度,得到三角形A'B'C'.
(1)在图中画出三角形A'B'C'；
(2)写出点A'、B'的坐标；
(3)求三角形ABC的面积.

答案：
(1)略　
(2)A'(0,4)　B'(-1,1)　
(3)6

20. (本小题满分12分)
甲、乙两人相约登山,他们同时从入口处出发,甲步行登山到山顶,乙先步行15分钟到缆车站,再乘坐缆车直达山顶. 甲、乙距山脚的垂直高度y(米)与甲登山的时间x(分钟)之间的函数图象如图所示.
(1)当15≤x≤40时,求乙距山脚的垂直高度y与x之间的函数关系式；
(2)求乙乘坐缆车上升过程中,和甲处于同一高度时距山脚的垂直高度.

答案： 解:
(1)由题图知,y与x之间的函数关系为一次函数,设解析式为y = kx + b,当x = 15时,y = 0,当x = 40时,y = 300,
∴$\begin{cases}15k + b = 0,\\40k + b = 300,\end{cases}$解得$\begin{cases}k = 12,\\b = -180,\end{cases}$
∴y与x之间的函数关系式为y = 12x - 180(15 ≤ x ≤ 40).
(2)当25 ≤ x ≤ 60时,设甲距山脚的垂直高度y与x之间的函数关系式为y = mx + n,当x = 25时,y = 160,当x = 60时,y = 300,
∴$\begin{cases}25m + n = 160,\\60m + n = 300,\end{cases}$解得$\begin{cases}m = 4,\\n = 60,\end{cases}$
∴y与x的函数关系式为y = 4x + 60,联立方程组$\begin{cases}y = 12x - 180,\\y = 4x + 60,\end{cases}$解得$\begin{cases}x = 30,\\y = 180,\end{cases}$
∴乙乘坐缆车上过程中,和甲处于同一高度时距山脚的垂直高度为180米(提示:两人在同一高度时距山脚的垂直高度,其实就是求两图象交点的纵坐标).