10. (1)如图①②,试探究$∠1,∠2与∠3,∠4$之间的数量关系;
(2)请你用文字描述上述关系;
(3)用你发现的结论解决问题:如图③,$AE,DE分别是四边形ABCD的外角∠NAD$,$∠MDA$的平分线,$∠B + ∠C = 240^{\circ}$,求$∠E$的度数.

(2)请你用文字描述上述关系;
(3)用你发现的结论解决问题:如图③,$AE,DE分别是四边形ABCD的外角∠NAD$,$∠MDA$的平分线,$∠B + ∠C = 240^{\circ}$,求$∠E$的度数.

答案:
解:
(1)设$\angle 1$的邻补角为$\angle 5$,$\angle 2$的邻补角为$\angle 6$.$\because \angle 3$,$\angle 4$,$\angle 5$,$\angle 6$是四边形的四个内角,$\therefore \angle 3 + \angle 4 + \angle 5 + \angle 6 = 360^{\circ}$.$\therefore \angle 3 + \angle 4 = 360^{\circ} - (\angle 5 + \angle 6)$.$\because \angle 1 + \angle 5 = 180^{\circ}$,$\angle 2 + \angle 6 = 180^{\circ}$,$\therefore \angle 1 + \angle 2 = 360^{\circ} - (\angle 5 + \angle 6)$.$\therefore \angle 1 + \angle 2 = \angle 3 + \angle 4$。
(2)在一个四边形中,两个外角的和等于与它们不相邻的两个内角的和。
(3)$\because \angle B + \angle C = 240^{\circ}$,$\therefore \angle MDA + \angle NAD = 240^{\circ}$.$\because AE$,$DE$分别是$\angle NAD$,$\angle MDA$的平分线,$\therefore \angle ADE = \frac{1}{2}\angle MDA$,$\angle DAE = \frac{1}{2}\angle NAD$.$\therefore \angle ADE + \angle DAE = \frac{1}{2}(\angle MDA + \angle NAD) = \frac{1}{2}× 240^{\circ} = 120^{\circ}$.$\therefore \angle E = 180^{\circ} - (\angle ADE + \angle DAE) = 60^{\circ}$。
(1)设$\angle 1$的邻补角为$\angle 5$,$\angle 2$的邻补角为$\angle 6$.$\because \angle 3$,$\angle 4$,$\angle 5$,$\angle 6$是四边形的四个内角,$\therefore \angle 3 + \angle 4 + \angle 5 + \angle 6 = 360^{\circ}$.$\therefore \angle 3 + \angle 4 = 360^{\circ} - (\angle 5 + \angle 6)$.$\because \angle 1 + \angle 5 = 180^{\circ}$,$\angle 2 + \angle 6 = 180^{\circ}$,$\therefore \angle 1 + \angle 2 = 360^{\circ} - (\angle 5 + \angle 6)$.$\therefore \angle 1 + \angle 2 = \angle 3 + \angle 4$。
(2)在一个四边形中,两个外角的和等于与它们不相邻的两个内角的和。
(3)$\because \angle B + \angle C = 240^{\circ}$,$\therefore \angle MDA + \angle NAD = 240^{\circ}$.$\because AE$,$DE$分别是$\angle NAD$,$\angle MDA$的平分线,$\therefore \angle ADE = \frac{1}{2}\angle MDA$,$\angle DAE = \frac{1}{2}\angle NAD$.$\therefore \angle ADE + \angle DAE = \frac{1}{2}(\angle MDA + \angle NAD) = \frac{1}{2}× 240^{\circ} = 120^{\circ}$.$\therefore \angle E = 180^{\circ} - (\angle ADE + \angle DAE) = 60^{\circ}$。
11. 为落实“双减”政策,丰富课后服务的内容,某学校计划到甲、乙两个体育专卖店购买一批新的体育用品,两个体育专卖店的优惠活动如下:
甲:所有商品按原价的8.5折出售;
乙:一次购买商品总额不超过300元的按原价付费,超过300元的部分打7折.
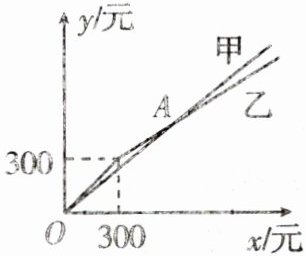
设需要购买体育用品的原价总额为$x$元,去甲体育专卖店购买实付$y_{甲}$元,去乙体育专卖店购买实付$y_{乙}$元,其函数图象如图所示.
(1)分别求出$y_{甲},y_{乙}关于x$的函数表达式;
(2)两图象交于点$A$,求点$A$的坐标;
(3)请根据函数图象,直接写出选择去哪个体育专卖店购买体育用品更合算.
甲:所有商品按原价的8.5折出售;
乙:一次购买商品总额不超过300元的按原价付费,超过300元的部分打7折.
设需要购买体育用品的原价总额为$x$元,去甲体育专卖店购买实付$y_{甲}$元,去乙体育专卖店购买实付$y_{乙}$元,其函数图象如图所示.
(1)分别求出$y_{甲},y_{乙}关于x$的函数表达式;
(2)两图象交于点$A$,求点$A$的坐标;
(3)请根据函数图象,直接写出选择去哪个体育专卖店购买体育用品更合算.

答案:
解:
(1)由题意可得$y_{甲} = 0.85x$.当$0\leq x\leq 300$时,$y_{乙} = x$;当$x > 300$时,$y_{乙} = 300 + (x - 300)× 0.7 = 0.7x + 90$.$\therefore y_{乙} = \left\{\begin{array}{l}x(0\leq x\leq 300),\\ 0.7x + 90(x > 300).\end{array}\right.$
(2)令$0.85x = 0.7x + 90$,解得$x = 600$.将$x = 600$代入$y_{甲} = 0.85x$,得$y_{甲} = 0.85× 600 = 510$,即点 A 的坐标为$(600,510)$。
(3)由图象可得,当________时,去甲体育专卖店购买体育用品更合算;当________时,去两个体育店购买体育用品一样合算;当________时,去乙体育专卖店购买体育用品更合算。
(1)由题意可得$y_{甲} = 0.85x$.当$0\leq x\leq 300$时,$y_{乙} = x$;当$x > 300$时,$y_{乙} = 300 + (x - 300)× 0.7 = 0.7x + 90$.$\therefore y_{乙} = \left\{\begin{array}{l}x(0\leq x\leq 300),\\ 0.7x + 90(x > 300).\end{array}\right.$
(2)令$0.85x = 0.7x + 90$,解得$x = 600$.将$x = 600$代入$y_{甲} = 0.85x$,得$y_{甲} = 0.85× 600 = 510$,即点 A 的坐标为$(600,510)$。
(3)由图象可得,当________时,去甲体育专卖店购买体育用品更合算;当________时,去两个体育店购买体育用品一样合算;当________时,去乙体育专卖店购买体育用品更合算。
查看更多完整答案,请扫码查看


